"Тригонометрические тождества"

Үй тапсырмасын тексеру:

№ 514

1)

2)

4)

№ 521

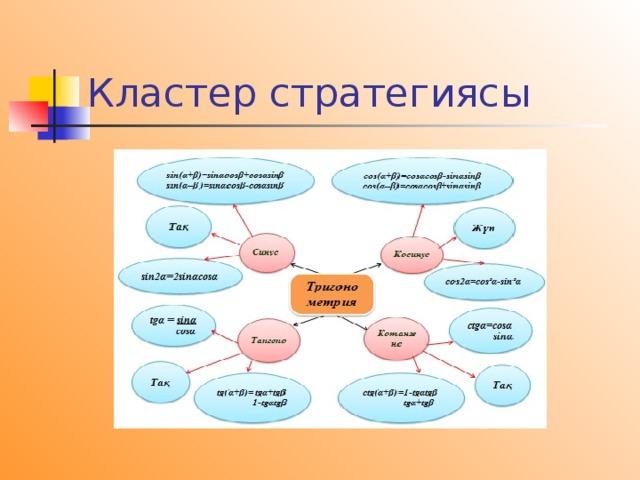
Кластер стратегиясы

Хип - хоп әдісі

Қосу формулалары

Қосуды көбейтуге, көбейтуді қосуға түрлендіру формулалары

Қос бұрыш пен жарты бұрыштың формулалары

№ 1.19; №2.1; №2.8; №2.10

• Дискриптор құру арқылы шығарамыз

Тест сұрақтары:

I. cos  =?

Тест сұрақтары:

II. sin2  =?

Тест сұрақтары:

III. tg  /2=?

Тест сұрақтары:

IV. tg2  =?

Тест сұрақтары:

V. Cos2  - cos 2  =?

Өзін өзі бағалау

Жаңа сабақ тақырыбы:

“ Тригонометриялық функциялардың көбейтіндісін қосындыға түрлендіру”

Қосу формулаларын еске түсірейік:

sin(  +  )=sin  cos  +cos  sin 

sin(  -  )=sin  cos  -cos  sin 

cos(  +  )=cos  cos  -sin  sin 

cos(  -  )=cos  cos  +sin  sin 

Sin(  +  )=sin  cos  +cos  sin 

sin(  -  )=sin  cos  -cos  sin 

мүшелеп қосып және азайтаймыз.

Қосамыз, сонда шығатыны төмендегідей:

sin(α+β)+sin(α-β)= 2 Sinαcosβ;

Бұдан:

sin α cos β =1/2[sin( α+β )+sin( α-β )]; (1)

Азайтамыз, сонда шығатыны төмендегідей:

sin(α+β)-sin(α-β)= cosαsinβ

Бұдан:

cos α sin β =1/2[sin( α+β )-sin( α-β )]; (2)

Сол сияқты,

cos(  +  )=cos  cos  -sin  sin 

cos(  -  )=cos  cos  +sin  sin 

мүшелеп қосып және азайтаймыз.

Қосамыз, сонда шығатыны төмендегідей:

cos(α+β)+cos(α-β) = 2cosαcosβ

Бұдан:

cos α cos β =1/2[cos( α+β )+cos( α-β )]; (3)

Азайтамыз, сонда шығатыны төмендегідей:

cos(α+β)-cos(α-β) = -2sinαsinβ

Бұдан:

sin α sin β =-1/2[cos( α+β )-cos( α-β )]; (4)

Тригонометриялық функциялардың көбейтіндісін қосындыға түрлендіру формулалары:

sin α cos β =1/2[sin( α+β )+sin( α-β )]; (1)

cos α sin β =1/2[sin( α+β )-sin( α-β )]; (2)

cos α cos β =1/2[cos( α+β )+cos( α-β )]; (3)

sin α sin β =-1/2[cos( α+β )-cos( α-β )]; (4)

Мысалдар:

sin α cos β =1/2[sin( α+β )+sin( α-β )]; (1)

cos α sin β =1/2[sin( α+β )-sin( α-β )]; (2)

cos α cos β =1/2[cos( α+β )+cos( α-β )]; (3)

sin α sin β =-1/2[cos( α+β )-cos( α-β )]; (4)

1 мысал: Өрнектің мәнін табайық.

2 мысал: Өрнектің мәндерін формулалардың және арнайы кестенің көмегімен есептейік.

2cos31 o sin14 o =sin(31 o +14 o )-sin(31 o -14 o )= =sin45 o -sin17 o =0,7071-0,2924=0,4147

Мысалдар:

sin α cos β =1/2[sin( α+β )+sin( α-β )]; (1)

cos α sin β =1/2[sin( α+β )-sin( α-β )]; (2)

cos α cos β =1/2[cos( α+β )+cos( α-β )]; (3)

sin α sin β =-1/2[cos( α+β )-cos( α-β )]; (4)

3 мысал: Тепе-теңдікті дәлелдейік.

4 мысал: Теңдікті дәлелдейік.

sin α cos β =1/2[sin( α+β )+sin( α-β )]; (1)

cos α sin β =1/2[sin( α+β )-sin( α-β )]; (2)

cos α cos β =1/2[cos( α+β )+cos( α-β )]; (3)

sin α sin β =-1/2[cos( α+β )-cos( α-β )]; (4)

Жаттығу жұмыстары:

І топ оқушыларына:

• . Sin15 о cos10 о
• . sin35 о sin50 о
• . 2sin2αcos5α

Көбейтіндіні қосындыға түрлендіріңдер .

II топ оқушыларына:

Өрнектерді қосындыға түрлендіріңдер, арнайы кестенің көмегімен мәндерін табыңдар.

• . Sin105 о cos75 о
• . 2cos37 о 30 / cos22 о 30 /
• . 4sin75 о cos15 о cos60 о

III топ оқушыларына:

Әуелі өрнекті түрлендіріп, одан соң арнайы кестені қолданып, мәндерін табыңдар.

1). 2sin70 о cos120 о +2cos68 о cos52 о

2). Cos86 о sin20 о -sin121 о sin59 о

3). Sin20 о cos70 о +sin10 о sin50 о

• 1). 2sin70 о cos120 о +2cos68 о cos52 о 2). Cos86 о sin20 о -sin121 о sin59 о 3). Sin20 о cos70 о +sin10 о sin50 о