Тригонометрические функции

ТРИГОНОМЕТРИЧЕСКИЕ ФУКЦИИ

СИНУС И КОСИНУС ЧИСЛА

Историческая справка

• Понятие синуса угла, как отношение отрезков треугольника появилось уже в 3 веке до нашей эры в работах математиков Древней Греции – Евклида, Архимеда, Апполония Пергского.
• В 1 веке нашей эры оно исследовалось Минелаем, но еще не получило своего сегодняшнего названия.

• В 4-5 веках индийский ученый Ариабхаты ввел специальный термин джива – «тетива», который при переводе арабских текстов на латынь был заменен синусом , что означает изгиб, кривизна.
• Слово косинус намного моложе. Косинус – это сокращение латинского выражения, которое означает «дополнительный синус».

Историческая справка

Абу-Абдалах, арабский астроном и математик 10 века, наблюдая за солнечными часами, создал первые таблицы таких тригонометрических функций, как тангенс и котангенс, не вводя эти понятия. Сам термин, в переводе с латинского означающий «отрезок касательной» был введен только в 1583 году датским математиком Томасом Финком.

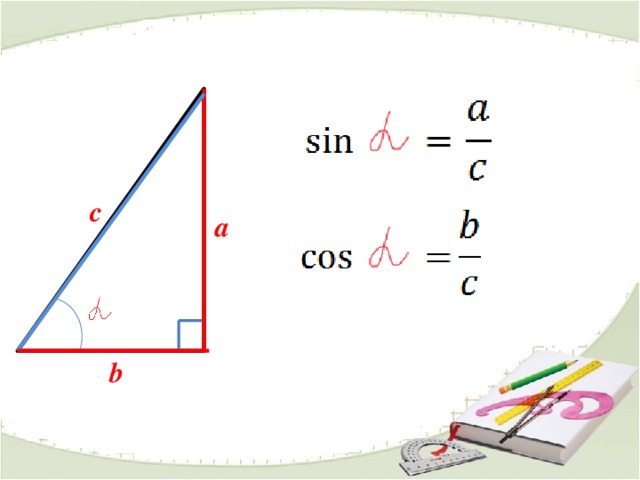
c

a

b

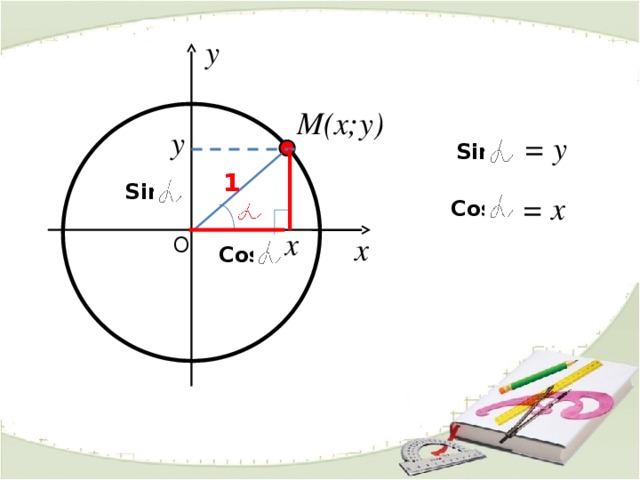
y

М(x;у)

y

= y

Sin

1

Sin

= x

Cos

x

x

O

Cos

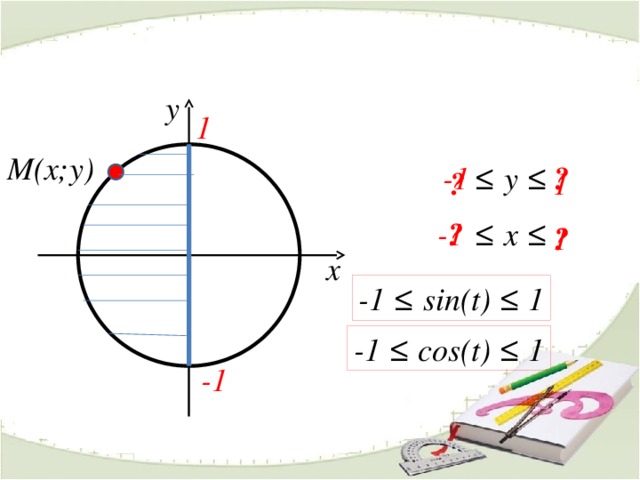
y

1

М(x;у)

?

-1

≤ у ≤

1

?

-1

≤ х ≤

?

1

?

x

-1 ≤ sin(t) ≤ 1

-1 ≤ cos(t) ≤ 1

-1

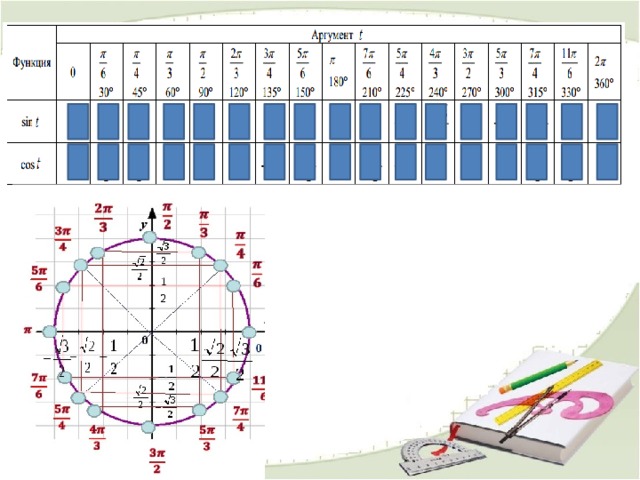
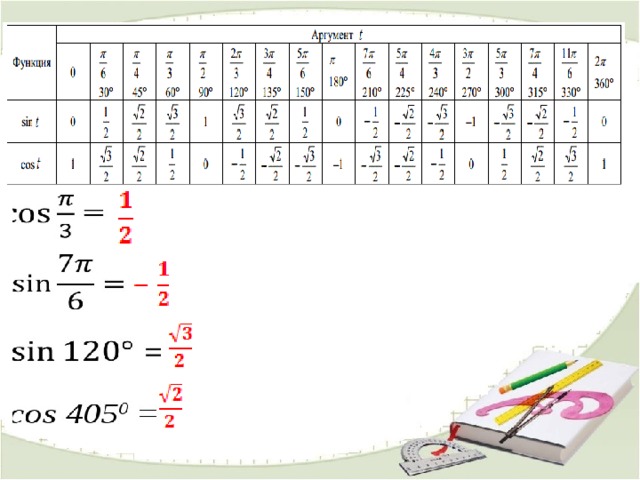
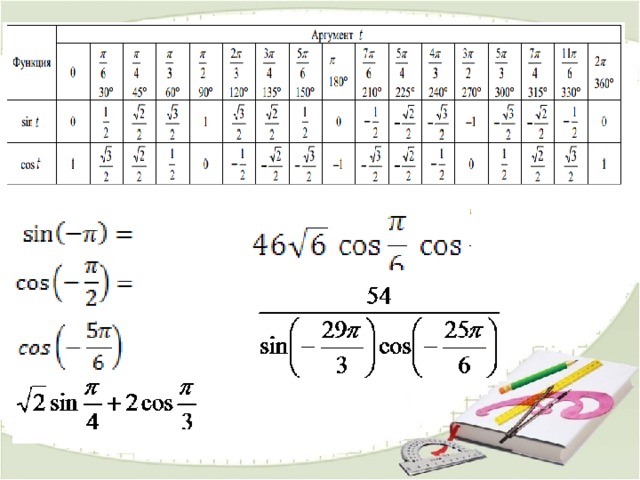
Домашнее задание

ТАНГЕНС И КОТАНГЕНС ЧИСЛА

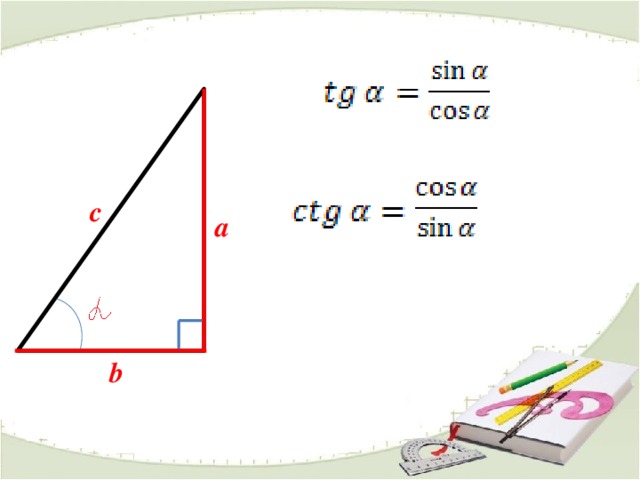
c

a

b

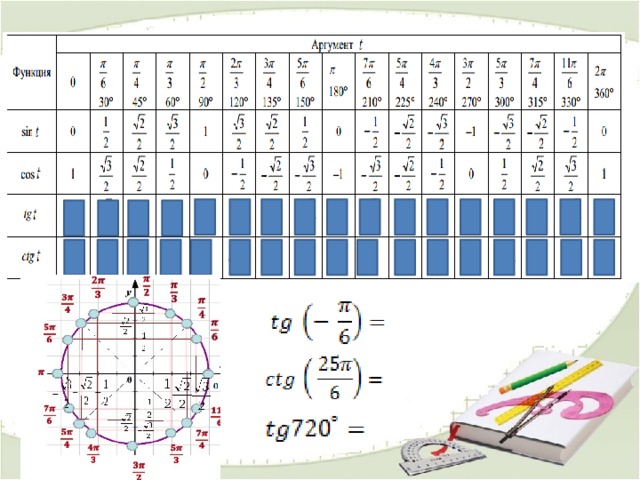
ДОМАШНЕЕ ЗАДАНИЕ

1)

6)

7)

2)

8)

3)

4)

9)

5)

10)