Тригонометрические функции числового аргумента.
График и свойства функции у = sin x.
Цели урока:
1. Повторить и систематизировать знания об основных тригонометрических формулах и их применении.
2. Ввести понятие функции у = sin x. Научиться строить график данной функции. Изучить свойства данной функции.
3. Совершенствовать умения применять основные формулы тригонометрии при решении примеров.
Дополнительное оборудование: компьютер, проектор, слайд-презентация к уроку, раздаточный материал на напечатанной основе с заданиями для самостоятельной работы.
Тип урока: комбинированный. Проверка знаний и умений студентов по пройденному материалу. Изложение нового материала. Первичное закрепление изученного учебного материала.
План урока:
1.Организационный момент, сообщение темы и цели урока.
2. Проверка домашнего задания.
3. Проверка знаний и умений по пройденному материалу.
4. Изложение нового материала.
5. Закрепление нового материала.
6. Применение полученных знаний.
7. Контроль и самопроверка.
8. Коррекция деятельности.
9. Подведение итогов.
10. Домашнее задание.
Х од урока
од урока
1. Организационный момент, сообщение темы и цели урока.
2. Проверка домашнего задания. Выборочно собрать тетради с домашним заданием у 3-4 студентов. Остальные, если не возникло вопросов по выполнению домашнего задания, в это время повторяют основные формулы тригонометрии.
3. Проверка знаний и умений по пройденному материалу.
Опрос - беседа по следующим вопросам:
1). Определение синуса, косинуса, тангенса и котангенса;
2). Градусная и радианная меры углов;
3). Знаки функций по четвертям.
1). Учитель: - Продолжая изучение алгебры, мы начали с вами знакомство с курсом алгебры и начал анализа. Первая тема, которую будем изучать – тригонометрические функции числового аргумента. В школьном курсе алгебры вам уже ввели понятия о данных функциях. Теперь мы должны будем подробно изучить каждую функцию, ее основные свойства, а также научиться строить графики этих функций. Кто мне скажет, сколько существует основных функций и как они называются?
Студенты:- Существует 4 основные функции тригонометрии: синус, косинус, тангенс и котангенс.
На интерактивной доске появляется слайд-презентация к этому вопросу.
Учитель: -Чтобы четко понимать, что же это за функции, и каким образом можно их получить, давайте рассмотрим треугольник АВС с острым углом α. Теперь, опираясь на свои знания по геометрии из школьного курса, дайте мне определение для каждой функции? На интерактивной доске появляется слайд-презентация к этому вопросу.
Студенты:
-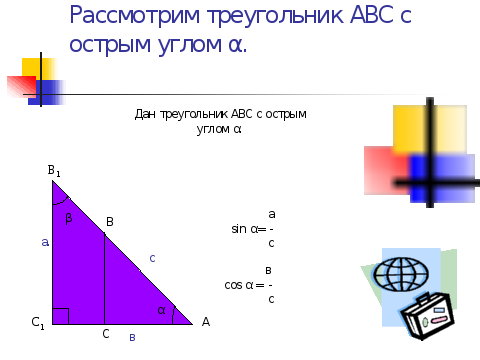 Синус угла α – это отношение противолежащего катета к гипотенузе. Косинус угла α – это отношение прилежащего катета к гипотенузе. Тангенс угла α – это отношение противолежащего катета к прилежащему. Котангенс угла α– это отношение прилежащего катета к противолежащему. Учитель: -Из данных определений функций следуют основные тригонометрические тождества (на интерактивной доске появляется слайд-презентация к этому вопросу)
Синус угла α – это отношение противолежащего катета к гипотенузе. Косинус угла α – это отношение прилежащего катета к гипотенузе. Тангенс угла α – это отношение противолежащего катета к прилежащему. Котангенс угла α– это отношение прилежащего катета к противолежащему. Учитель: -Из данных определений функций следуют основные тригонометрические тождества (на интерактивной доске появляется слайд-презентация к этому вопросу)
 Запишите их в тетради. К ним мы вернемся позже, а пока рассмотрим следующий вопрос.
Запишите их в тетради. К ним мы вернемся позже, а пока рассмотрим следующий вопрос.
Если мы изобразим треугольник АВ1С1 подобный данному, с фиксированным углом α, то нетрудно увидеть, что синус и косинус зависят лишь от угла α и не зависят от размеров треугольника.
П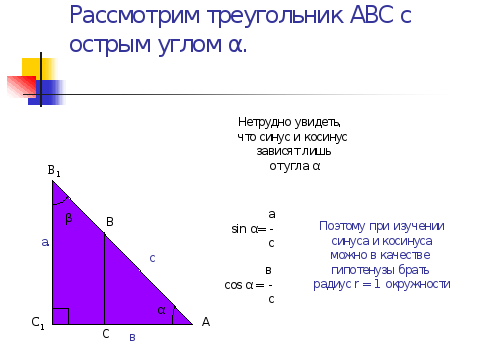
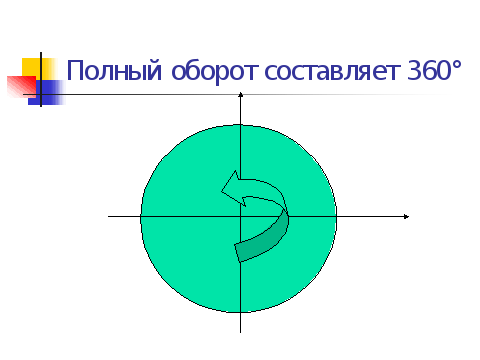 оэтому при изучении свойств синуса и косинуса можно в качестве гипотенузы брать радиус r = 1 окружности, т. е. отсчитывать углы, пользуясь единичной окружностью. Если полный оборот такого радиуса относительно центра круга считать углом в 360°, то ясно, что любой угол можно измерить в градусах. Обычно отсчет ведется от направления оси Ох, начиная от 0°, причем поворот радиуса против часовой стрелки считается положительным, а по часовой стрелке - отрицательным.
оэтому при изучении свойств синуса и косинуса можно в качестве гипотенузы брать радиус r = 1 окружности, т. е. отсчитывать углы, пользуясь единичной окружностью. Если полный оборот такого радиуса относительно центра круга считать углом в 360°, то ясно, что любой угол можно измерить в градусах. Обычно отсчет ведется от направления оси Ох, начиная от 0°, причем поворот радиуса против часовой стрелки считается положительным, а по часовой стрелке - отрицательным.
 2). Вот мы подошли ко второму вопросу, поставленному перед нами, - градусной и радианной мерам углов. Как оказалось на практике, градусная мера угла не всегда удобна, прежде всего потому, что определенные ранее нами синус и косинус не попадают в класс функций действительного переменного, для которых аргументом являются числа, а не элементы других множеств (в данном случае углов, поскольку
2). Вот мы подошли ко второму вопросу, поставленному перед нами, - градусной и радианной мерам углов. Как оказалось на практике, градусная мера угла не всегда удобна, прежде всего потому, что определенные ранее нами синус и косинус не попадают в класс функций действительного переменного, для которых аргументом являются числа, а не элементы других множеств (в данном случае углов, поскольку
1 градус- это угол, получаемый в результате разделения круга радиусом на 360 равных частей). Например, если числа мы можем умножать и складывать, то с углами проделать те же операции невозможно. В итоге запись sin (α · β), где α и β – углы, смысла иметь не будет.
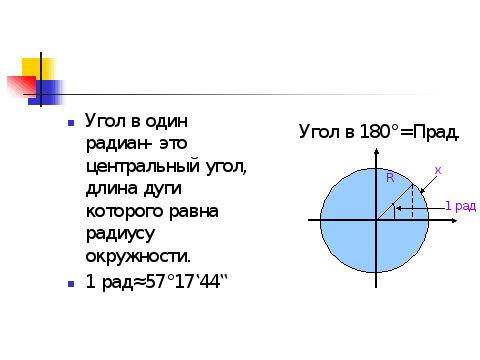
Поэтому вводят еще числовую меру углов, называемую радианной.. Делается это путем построения
следующего изображения (на интерактивной доске появляется слайд-презентация к этому вопросу).
Каждому углу α сопоставляется длина дуги х единичной окружности. Например, при α = 90° х = π/2; при α = 45° х = π/4; при α = 180° х = π.
3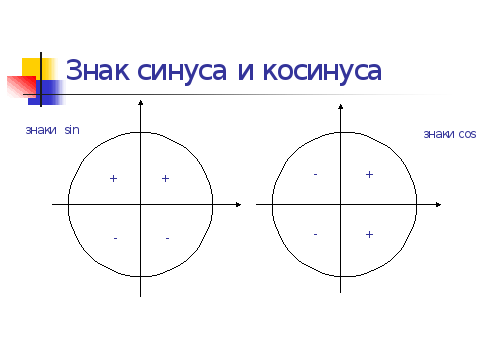 ). И, наконец, третий вопрос - знаки функций по четвертям.
). И, наконец, третий вопрос - знаки функций по четвертям.
Первоначально знаки синуса и косинуса были определены лишь для острых углов. Теперь появляется возможность расширить это определение. Для этого достаточно поместить центр окружности в начало координат и брать величины а и b в соответствии с теми знаками, которые будут иметь проекции точек окружности на оси координат.
(на интерактивной доске появляется слайд-презентация по данному вопросу).
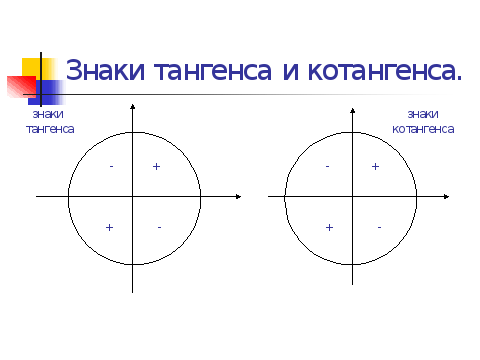 Таким образом, знаки функций по четвертям будут располагаться следующим образом:
Таким образом, знаки функций по четвертям будут располагаться следующим образом:
(на интерактивной доске появляется слайд-презентация по данному вопросу)
Аналогично можно рассчитать знаки для тангенса и котангенса.
Также для дальнейшего изучения материала вам понадобится знание таблицы значений тригонометрических функций. Ее вы тоже изучали в рамках школьного курса. Заданием вам на дом было повторение данной таблицы. Чтобы проверить, как вы справились с ним, я предлагаю вам заполнить следующие таблицы. В одной колонке уже вписаны значения радианной меры углов, в другой вы самостоятельно дописываете то значение функции, которое она будет принимать.
| sin π/2
|
|
| sin 5π/6 |
|
| sin π/4
|
| sin π/2 |
| |
| cos 3π/2
|
| cos π/3 |
| |
| cos π
|
| cos 2π |
| |
| sin π/6
|
| sin 4π/3 |
| |
| tg π/2
|
| tg π/6 |
| |
| tg 5π/6
|
| tg 7π/6 |
| |
| ctg 0
|
| ctg π |
| |
| ctg π/4
|
| ctg π/2 |
| |
| cos π/2
|
| cos 3π/4 |
|
4. Изложение нового материала. Функция у = sin x.
Учитель:- Давай с вами сначала вспомним, что же такое функция? Кто даст мне точное определение функции?
Студенты:- Функция – это зависимость переменной У от переменной Х, причем такая, что каждому значению переменной Х соответствует единственное значение переменной У.
Учитель:- Совершенно верно. Так как мы для удобства ввели радианную меру углов, то, основываясь на это, строят график функции синуса. Делается это путем построения следующего отображения множества углов в числовое множество. Другими словами градусы переводят в числа.
Рассмотрим функцию у = sin x. Теперь дадим определение этой функции. Числовая функция, заданная формулой у = sin x, называется синусом. Запишите определение синуса в тетради.
Свойства функции у = sin x.
Учитель:- Рассмотрим свойства функции у = sin x. (на интерактивной доске появляется слайд- презентация по данному вопросу)
1 ) Область определения этой функции – множество всех действительных чисел.
) Область определения этой функции – множество всех действительных чисел.
Обозначается: D (sin x) = R.
(R – множество всех действительных чисел)
2) Областью значения функции синус является отрезок [- 1; 1], поскольку и ординаты, и абсциссы точек единичной окружности принимают все значения от -1 до 1.
Обозначается: Е (sin x) = [- 1; 1].
3) Следовательно, функция имеет период 2π, т. е. ее значения повторяются при сдвиге аргумента вдоль оси 0х на любое число, кратное 2π. Отсюда следует еще одно свойство функции синуса:
sin (x + 2πn) = sin x (n – произвольное целое число);
3) Еще известными свойствами этой функции является то, что для любого х справедливы следующие равенства:
sin (-x) = - sin x;
sin x = 0, при х = πn, n € Z (Z – множество всех целых чисел);
sin x = 1, при х = π/2 + 2πn, n € Z;
sin x = -1, при х = - π/2 + 2πn, n € Z;
Исходя из этих свойств функции, можно сделать вывод:
1) на отрезке [- π/2; π/2] функция синуса является строго монотонно возрастающей;
2) функция четная;
3) периодическая, с установленным периодом 2π.
4) функция непрерывна.
График функции у = sin x.
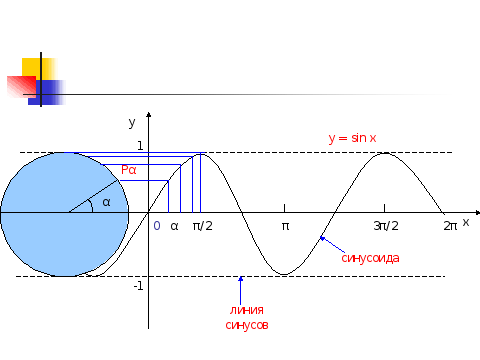
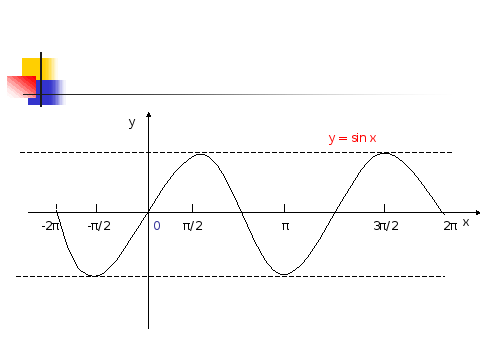 Построим теперь график функции синуса на отрезке [0; 2π]. Для этого отметим на оси ординат точки с координатами (0;-1) и (0;1), а на оси абсцисс - точку с абсциссой 2π. Для построения точки графика с абсциссой α воспользуемся определением синуса на множестве действительных чисел. Отметим точку Рα на единичной окружности и проведем через эту точку прямую, параллельную оси абсцисс (0х). Точка пересечения этой прямой и прямой х = α искомая, так как ее ордината совпадает с ординатой точки Pα, а по определению sin α равен ординате Рα (на интерактивной доске появляется слайд-презентация по данному вопросу).
Построим теперь график функции синуса на отрезке [0; 2π]. Для этого отметим на оси ординат точки с координатами (0;-1) и (0;1), а на оси абсцисс - точку с абсциссой 2π. Для построения точки графика с абсциссой α воспользуемся определением синуса на множестве действительных чисел. Отметим точку Рα на единичной окружности и проведем через эту точку прямую, параллельную оси абсцисс (0х). Точка пересечения этой прямой и прямой х = α искомая, так как ее ордината совпадает с ординатой точки Pα, а по определению sin α равен ординате Рα (на интерактивной доске появляется слайд-презентация по данному вопросу).
На рисунке показано построение нескольких точек графика. Соединяя их плавной линией, получаем эскиз графика функции синуса на отрезке [0; 2π]. А так как из свойств этой функции мы знаем, что синус – функция периодическая с установленным периодом 2π, то на всей прямой с помощью параллельных переносов вдоль оси 0х (вправо и влево) строим график функции.
Определение: график функции у = sin x называется синусоидой. Отрезок [- 1; 1] оси ординат, с помощью которого мы находим значения синуса, иногда называют линией синусов (на интерактивной доске появляется слайд-презентация по данному вопросу).
5. Закрепление нового материала.
Учитель: -Ребята, мы с вами рассмотрели числовую функцию, заданную формулой у = sin x. Разобрались, какими свойствами обладает данная функция, научились строить ее график. А теперь ответьте мне на следующие вопросы:
а) какой период задан для функции синуса?
б) зачем вводится радианная мера углов?
в) какой отрезок является областью значения для данной функции?
Студенты: а) 2π
б) градусная мера угла не всегда удобна, поэтому вводят еще числовую меру углов, называемую радианной.
в) [- 1; 1]
Как видно из ваших ответов, данную тему вы усвоили хорошо.
6. Применение полученных знаний.
Учитель: -Теперь попробуем с вами применить полученные знания при выполнении заданий.
Задание: Найдите область определения и область значения функции у = 2 sin x. Постройте ее график (на интерактивной доске появляется слайд-презентация к данному заданию).
З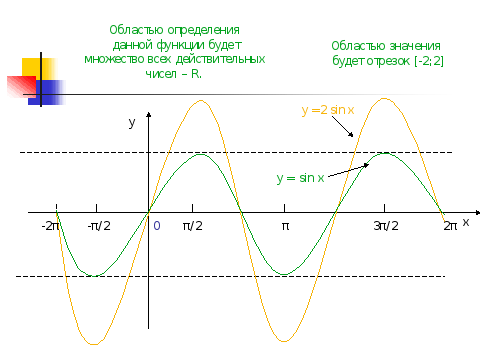 адания для самостоятельной работы:
адания для самостоятельной работы:
І вариант
Найдите область определения и область значения функции у = 1/2 sin x. Постройте ее график.
ІІ вариант
Найдите область определения и область значения функции у = 3 sin x. Постройте ее график.
7. Контроль и самопроверка.
Учитель:- Ребята, а теперь поменяйтесь тетрадями и самостоятельно проверьте друг у друга, правильно ли выполнены задания.
8. Коррекция деятельности.
Выяснить какие возникли проблемы или недочеты во время выполнения заданий самостоятельной работы.
9. Подведение итогов.
Учитель:
1. -Ребята, сегодня наше занятие, на мой взгляд, прошло результативно. Вами хорошо усвоена данная тема. Вы с успехом справились с поставленными перед вами целями. То есть,:1) повторили и систематизировали знания о мерах углов, понятии синуса, косинуса, тангенса и котангенса;
2) ввели понятие функции синуса;
3) научились строить график функции у = sin x;
4) изучили свойства функции у = sin x.
2. Выставление оценок.
10. Домашнее задание.
Д/З под запись: 1) выучить свойства функции у = sin x;
2) найдите область определения и область значения функций: у = -1/2 sin x, у = sin 3x, у =3 + sin x; постройте их графики. (Задание сопровождается комментарием преподавателя).
.
8

 Получите свидетельство
Получите свидетельство Вход
Вход












 Тригонометрические функции числового аргумента. График и свойства функции у = sin x. (780 KB)
Тригонометрические функции числового аргумента. График и свойства функции у = sin x. (780 KB)
 0
0 751
751 16
16 Нравится
0
Нравится
0


