Цели:
1. Обучающая: обобщить, систематизировать, расширить и углубить знания учащихся о треугольнике, закрепить навыки и умения при решения задач, используя определения и теоремы по данной теме.
2. Развивающая: развивать математическую речь учащихся, их память, внимание, наблюдательность, умение сравнивать, обобщать, обосновано делать выводы, развивать умение преодолевать трудности при решении задач, а также познавательный интерес учащихся.
3. Воспитывающая: воспитание навыков контроля и самоконтроля, воспитание правильной самооценки, аккуратности, внимательности, положительное отношение к обучению.
Задачи:
1. Образовательная: знать определения и теоремы по данной теме, применять теоретические знания при решении устных, письменных и тестовых задач.
2. Развивающие: умения выделять главное и существенное, сравнивать и обобщать имеющиеся знания, планировать и контролировать свою деятельность при выполнении заданий, развитие зрительной и слуховой памяти, внимания, математической речи и логического мышления.
3. Воспитательные: воспитания трудолюбия, усидчивости, умения слушать других, умения высказывать свою точку зрения, проводить рассуждения, доказательства при выполнении заданий.
Оборудование: интерактивная доска.
Учебник:«Геометрия-7-9» Л.С.Атанасян.2009г.;методпособие к учебному комплекту Л.С.Атанасян и др. (М:Просвещение);учебно-методическая газета «Математика»
Тип урока: урок обобщения и закрепления.

ХОД УРОКА.
1. Организационный момент. (2 слайд)
Сегодня на уроке мы с вами обобщим наши знания по теме «Треугольник», повторим определения и теоремы по данной теме, а также применим все наши знания для решения устных, письменных и тестовых задач.
Девизом нашего урока я взяла слова Александра Сергеевича Пушкина «Вдохновение нужно в геометрии, как в поэзии». Все стихи А.С.Пушкина побуждают к размышлениям, в том числе о смысле жизни: «Но не хочу, о други, умирать;
Я жить хочу, чтоб мыслить и страдать».
Поэт хочет жить! Жить, чтобы в первую очередь мыслить. Призываю вас всех сегодня мыслить на уроке!!!
2. Исторический материал .Игра «Колесо истории» (3 слайд ).
Игра составлена аналогично телевизионной игре. В сценках используются костюмы и атрибуты, близкие данному веку.
Ведущей. Математическая игра начинается в Древней Греции (VI в. до н.э.).
1. Фалес и Пифагор.
(Фалес беседует с юным Пифагором.)
П.Фалес из Милета, ты не был на родине два года. В какой стране ты был?
Ф.Страна, в которой я побывал, прекрасна. Я привез немало диковинных вещей. Но восхитило меня не они.
П. Что же восхитило тебя, Фалес?
Ф. О! Меня восхитили гарпедонапты.
П. Это такие звери?
Ф. Нет. Это люди. Землемеры - геометры.
П. Чем они восхитили тебя?
Ф. Знаниями. Они так много умеют: измерять и находить площади и объемы; делить отрезок на равные части циркулем; у них есть треугольник со сторонами 3, 4 и 5 локтей. Стороны его – гипотенуза и катеты.
2. Защитник Сиракуз (рассказ об Архимеде).
В. Зарождение геометрии (заключительное слово).
3.Актуализация знаний.
1.Повторить признаки равенства треугольников (слайды 4, 5).
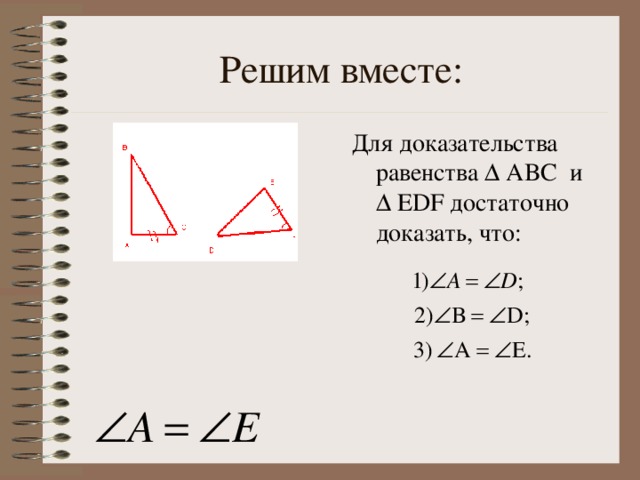
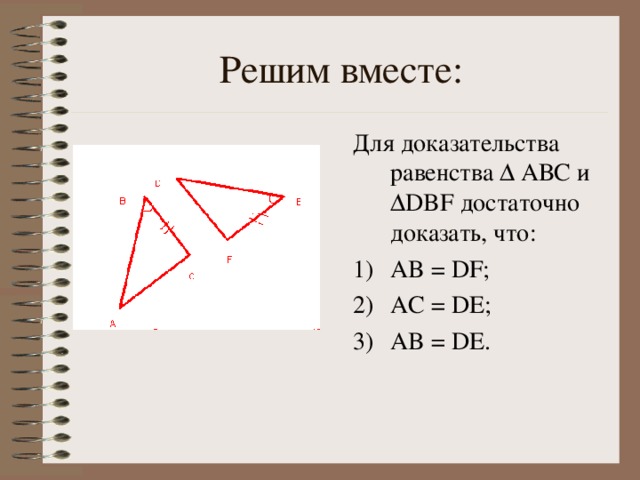
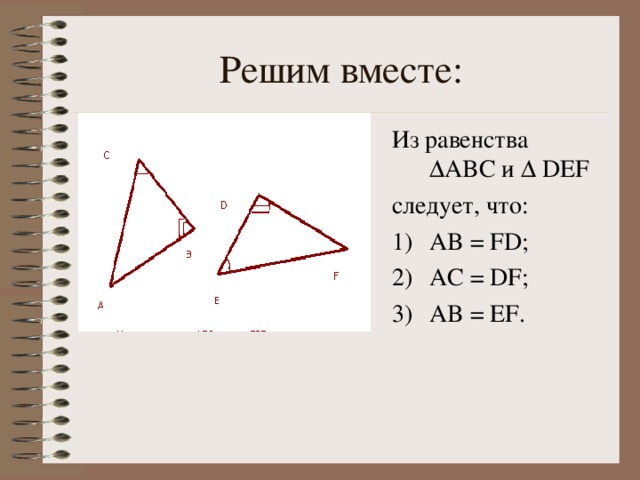
2.Решим вместе (слайды 6, 7 и 8).
3.Тест (слайды 9, 10 и 11).
4.Закрепление.
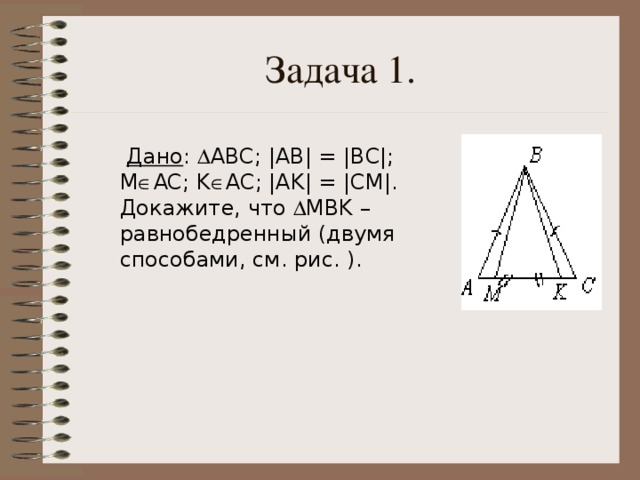
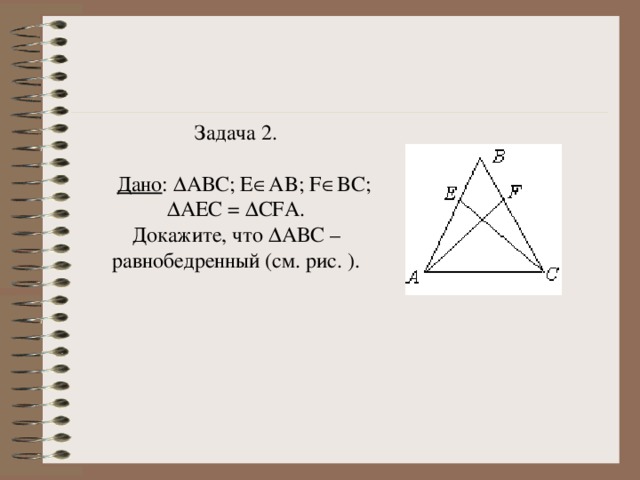
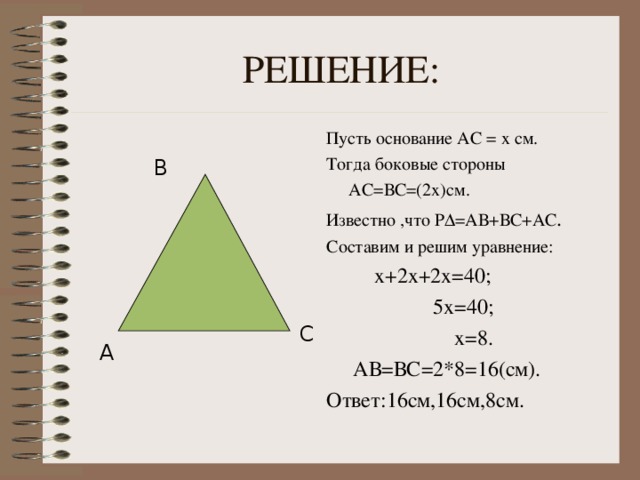
1.Решите задачу (на интерактивной доске и в тетрадях, слайды 12, 13, 14 и 15).
Физкульминутка (слайд 16).
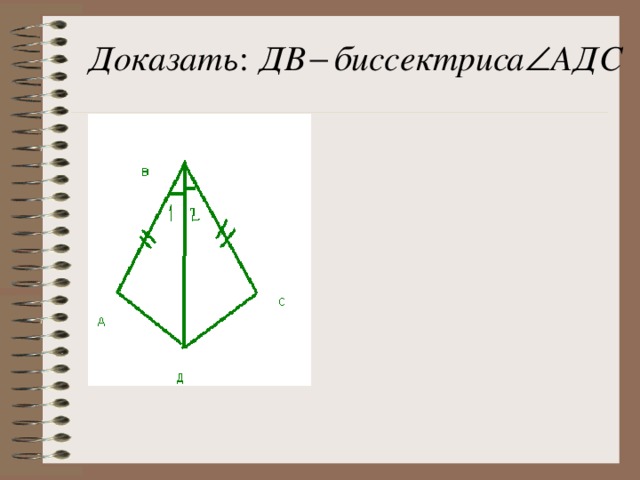
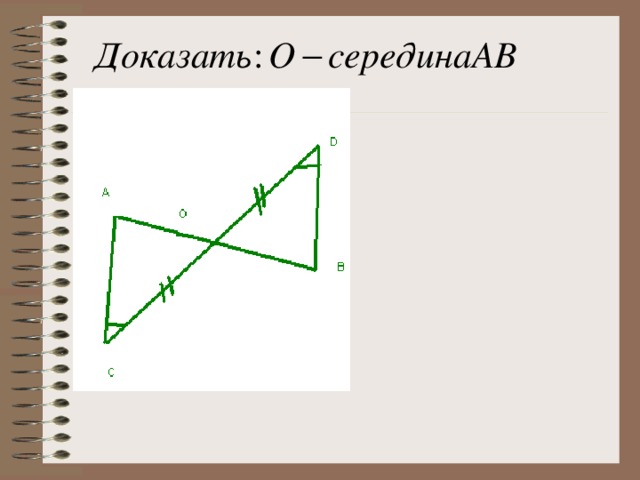
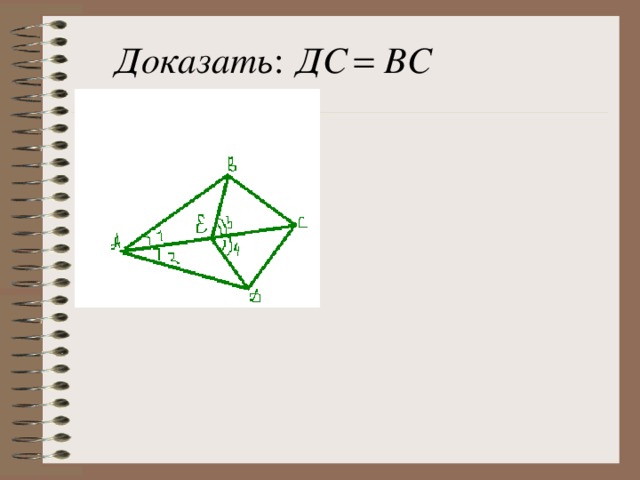
2.Докажите (на интерактивной доске и в тетрадях, слайды 17, 18 и 19).
3.Решите задачу (слайды 20, 21).
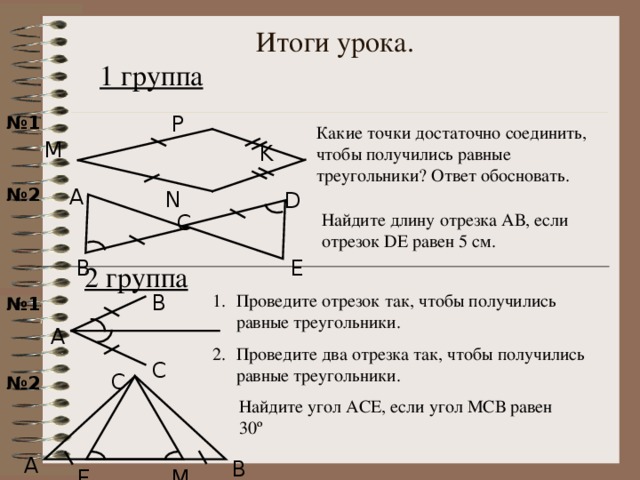
5.Итоги урока (слайд 22).
6.Домашнее задание (слайд 23).
7.Выставление оценок (слайд 24).

 Получите свидетельство
Получите свидетельство Вход
Вход










![Задача 3. Стороны равностороннего треугольника АВС делятся точками K , L и M в одном и том же отношении (считая по часовой стрелке). Докажите, что треугольник KLM – равносторонний. Дано : АВС; |АВ| = |ВС| = |АС|; K [ AB ]; L [ BC ]; M [ AC ]; | AK |:| KB | = | BL |:| LC | =| CM |:| MA |. Доказать : | MK | = | KL | = | LM |.](https://fsd.videouroki.net/html/2013/10/01/98665509/img13.jpg)














 Треугольники. Признаки равенства треугольников (1.03 MB)
Треугольники. Признаки равенства треугольников (1.03 MB)
 0
0 648
648 40
40 Нравится
0
Нравится
0









