Тренажер по теме : « ТРАПЕЦИЯ ».
При решении группы задач воспользуйтесь данными свойствами. Решив задачу найдите ее кодовую букву и внесите в таблицу ответов. По окончании работы вы получите зашифрованную фразу.
Свойство 1. Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна средней линии.
Свойство 2. Высота равнобедренной трапеции, в которую можно вписать окружность, является средним геометрическим её оснований: h2 = a ∙ b.
Свойство 3. В равнобедренной трапеции проекция диагонали на большее основание равна средней линии трапеции.
Свойство 4. Если в равнобедренной трапеции диагонали взаимно перпендикулярны, то её высота равна средней линии.
Свойство 5.Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты S = h2.
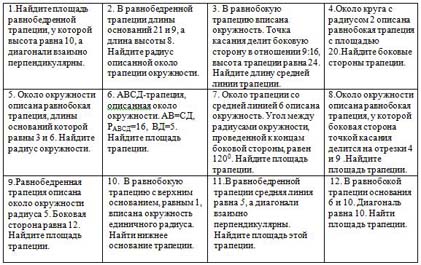
| 1.Найдите площадь равнобедренной трапеции, у которой высота равна 10, а диагонали взаимно перпендикулярны. | 2. В равнобедренной трапеции длины оснований 21 и 9, а длина высоты 8. Найдите радиус описанной около трапеции окружности. | 3. В равнобокую трапецию вписана окружность. Точка касания делит боковую сторону в отношении 9:16, высота трапеции равна 24. Найдите длину средней линии трапеции. | 4.Около круга с радиусом 2 описана равнобокая трапеция с площадью 20.Найдите боковые стороны трапеции. |
| 5. Около окружности описана равнобокая трапеция, длины оснований которой равны 3 и 6. Найдите радиус окружности. | 6. АВСД-трапеция, описанная около окружности. АВ=СД, РАВСД=16, ВД=5. Найдите площадь трапеции. | 7. Около трапеции со средней линией 6 описана окружность. Угол между радиусами окружности, проведенной к концам боковой стороны, равен 1200. Найдите площадь трапеции. | 8.Около окружности описана равнобокая трапеция, у которой боковая сторона точкой касания делится на отрезки 4 и 9 .Найдите площадь трапеции. |
| 9.Равнобедренная трапеция описана около окружности радиуса 5. Боковая сторона равна 12. Найдите площадь трапеции.
| 10. В равнобокую трапецию с верхним основанием, равным 1, вписана окружность единичного радиуса. Найти нижнее основание трапеции.
| 11.В равнобедренной трапеции средняя линия равна 5, а диагонали взаимно перпендикулярны. Найдите площадь этой трапеции.
| 12. В равнобокой трапеции основания 6 и 10. Диагональ равна 10. Найти площадь трапеции.
|
| Т | р | а | п | е | ц | и | ю | - | З | н | а | Й |
| 100 | 85/8 | 25 | 5 | 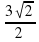
| 12 | 36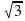 | 156 |
| 120 | 4 | 25 | 48 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | - | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Й-48 А-25 И-36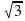 Е-
Е-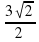 Ц-12 Ю-156 Н-4 Т-100 З-120 Р-85/8 П-5
Ц-12 Ю-156 Н-4 Т-100 З-120 Р-85/8 П-5

 Получите свидетельство
Получите свидетельство Вход
Вход











 Тренажер по математике по теме "Трапеция" (20.11 КB)
Тренажер по математике по теме "Трапеция" (20.11 КB)
 0
0 878
878 57
57 Нравится
0
Нравится
0



