МНОГОУГОЛЬНИКИ.
У многоугольника стороны могут пересекаться, а могут не пересекаться.
Смежные отрезки многоугольника лежат на одной прямой.
Две смежные стороны многоугольника имеют одну общую вершину.
Название многоугольника зависит от количества вершин.
Количество сторон многоугольника не зависит от количества его вершин.
Периметр многоугольника – это сумма длин всех его сторон.
Соседние вершины многоугольника лежат на разных сторонах.
Отрезок, соединяющий любые две соседние вершины, называют диагональю многоугольника.
Любой многоугольник разделяет плоскость на внешнюю и внутреннюю области.
Многоугольник состоит из сторон многоугольника и его внутренней области.
Верно ли, что многоугольники бывают выпуклые и невыпуклые.
Прямая, проходящая через любую сторону выпуклого многоугольника разделяет его на две части.
Невыпуклый многоугольник находится по одну строну от прямой, проходящей через любую его сторону.
Верно ли, что у многоугольника углов столько же, сколько и сторон.
У четырехугольника и сторон, и углов, и вершин – четыре.
Соседние стороны четырехугольника называют противоположными.
Противоположные вершины четырехугольника не являются соседними.
Четырехугольники бывают только выпуклые.
У четырехугольника можно провести четыре диагонали.
Каждая диагональ разбивает четырехугольник на два треугольника.
Сумма углов любого выпуклого четырехугольника, параллелограмма и трапеции равна 3600.
У параллелограмма соседние стороны параллельны и равны.
У параллелограмма противоположные углы равны.
Диагонали параллелограмма точкой пересечения не делятся пополам.
У трапеции противоположные стороны параллельны.
Основания трапеции между собой равны.
Боковые стороны равнобедренной трапеции между собой равны.
У прямоугольной трапеции три угла прямые.
КЛЮЧ:
«+» - 3; 4; 6; 9; 10; 11; 14; 15; 17; 20; 21; 23; 27;
«-» - 1; 2; 5; 7; 8; 12; 13; 16; 18; 19; 22; 24; 25; 26; 28
ОЦЕНКИ:
«3» - 15 – 19
«4» - 20 – 25
«»5 – 26 – 28
ТЕМА: Площадь.
Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
За единицу измерения площадей принимают только квадрат со стороной 1 см.
Площадь многоугольника выражается только положительной величиной.
Верно ли, что равные многоугольники имеют равные площади?
Если многоугольник разбит на части, то его площадь равна сумме площадей этих частей.
Площадь квадрата равна кубу его стороны.
Площадь прямоугольника равна половине произведения его противоположных сторон.
Площадь прямоугольника равна произведению его соседних сторон.
Основание – это одна из сторон параллелограмма.
Высота треугольника – это перпендикуляр, опущенный из любой точки противоположной стороны к прямой, содержащей основание.
Площадь параллелограмма равна половине произведения высоты на основание.
Одну из сторон треугольника называют основанием.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна произведению его катетов.
Если основания двух треугольников равны, то их площади относятся как высоты.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Высота трапеции – это перпендикуляр, проведенный к боковой стороне.
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Площадь ромба равна произведению его диагоналей.
Площадь ромба можно найти по той же формуле, что и параллелограмм.
Теорема Пифагора используется в любых треугольниках.
В прямоугольном треугольнике квадрат любого катета равен сумме квадратов гипотенузы и другого катета.
Пифагоровы треугольники те, у которых длины сторон выражаются целыми числами.
Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
КЛЮЧ:
«+» - 1; 3; 4; 5; 8; 9; 10; 12; 13; 16; 18; 20; 23; 24
«-» - 2; 6; 7; 11; 14; 15; 17; 19; 21; 22;
ОЦЕНКИ:
«3» - 12 – 16
«4» - 17 – 21
«5»– 22 – 24
ТЕМА: «Определение подобных треугольников. Признаки подобия треугольников»
Верно ли, что отношение двух отрезков – это деление одного отрезка на другой?
Если одна пара отрезков пропорциональна другой паре отрезков, то их отношения не равны.
Понятие пропорциональность рассматривается только на примере двух отрезков.
В геометрии фигуры одинаковой формы принято называть подобными.
Если у двух треугольников АВС и А1В1С1 соответствующие углы равны, то стороны АВ и В1С1 называют сходственными.
Два треугольника называют подобными, если их углы соответственно равны, а стороны одного треугольника соответственно пропорциональны сторонам другого.
Коэффициент подобия – это число, равное отношению сходственных сторон подобных треугольников.
Подобие треугольников нельзя установить, если известно, что некоторые углы соответственно равны или некоторые стороны пропорциональны.
Площади двух подобных треугольников относятся как коэффициент подобия в квадрате.
Отношение периметров двух подобных треугольников равно коэффициенту подобия в квадрате.
По первому признаку подобия треугольников необходимо указать две пропорциональные стороны и угол между ними.
По второму признаку подобия треугольников необходимо указать два равных угла в каждом треугольнике.
По третьему признаку подобия треугольников необходимо указать пропорциональность трех сторон.
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
КЛЮЧ:
«+» - 1; 4; 6; 7; 9; 13; 14
«-» - 2; 3; 5; 8; 10; 11; 12
ОЦЕНКИ:
«3» - 7 – 9
«4» - 10 – 12
«5»– 13 – 14
ТЕМА : «Применение подобия к доказательству теорем и решению задач»
1) Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
2) В любом треугольнике можно провести только одну среднюю линию.
3) Средняя линия треугольника параллельна одной из его сторон и равна ее половине.
4) Средняя линия треугольника отсекает от первоначального треугольника подобный ему треугольник.
5) Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от конца медианы.
6) Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет его на два прямоугольных треугольника не подобных данному треугольнику.
7) Отрезок MN называют средним пропорциональным для двух отрезков АВ и CD, если он равен квадратному корню из суммы этих отрезков.
8) Высота прямоугольного треугольника, проведенная из любой вершины, есть среднее пропорциональное для отрезков, на которые делится катет.
9) Катетпрямоугольного треугольника, проведенный из вершины прямого угла, есть среднее пропорциональное для гипотенузы и проекции этого катета на гипотенузу.
10) Метод подобия нельзя применить для решения задач на построение треугольников.
11) Измерительные работы на местности можно провести с помощью подобия двух прямоугольных треугольников.
12) Фигуры F и F1 называют подобными, если для любых двух точек этих фигур выполняется равенство 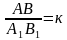 .
.
13) Коэффициент подобия – это число, равное отношению сходственных сторон подобных фигур.
14) Верно ли, что если ширина одного прямоугольника больше в 2 раза ширины подобного ему прямоугольника, то длина может быть в 3 раза.
КЛЮЧ:
«+» - 1; 3; 4; 9; 11; 12: 13;
«-» - 2; 5; 6; 7; 8; 10; 14
ОЦЕНКИ:
«3» - 7 – 9
«4» - 10 – 12
«5»– 13 – 14
ТЕМА: «Окружность»
1) Верно ли, что возможны три случая взаимного расположения прямой и окружности.
2) Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность имеют две общих точки.
3) Прямая называется касательной, если расстояние от центра окружности до прямой равно радиусу окружности.
4) По свойству: радиус окружности, проведенный в точку касания перпендикулярен к касательной.
5) Отрезки касательных к окружности, проведенные из одной точки равны.
6) Верно ли, что прямая проходящая через конец диаметра, лежащий на окружности и перпендикулярна к этому диаметру, то она является касательной.
7) На окружности можно построить дугу любой градусной меры.
8) Центральный угол – это угол, одна сторона которого является диаметром.
9) Если центральный угол развернутый, то его соответствующая дуга называется полуокружностью.
10) Если центральный угол больше развернутого, то соответствующая дуга меньше полуокружности.
11) Градусная мера дуги – это градусная мера соответствующего центрального угла.
12) Вписанный угол – это угол, вершиной которого является центр окружности.
13) Говорят, что вписанный угол опирается на дугу, если она не лежит внутри вписанного угла.
14) Вписанный угол равен половине дуги, на которую он опирается.
15) Вписанный угол равен центральному углу.
16) Вписанные углы, опирающиеся на одну и ту же дугу не равны.
17) Вписанный угол, опирающийся на диаметр – прямой.
18) Каждая точка биссектрисы неразвернутого угла находится на разном расстоянии от его сторон.
19) Всего существует четыре замечательных точки треугольника.
20) Вписанная окружность касается всех сторон многоугольника.
21) Все вершины вписанного многоугольника лежат внутри окружности.
22) В любой четырехугольник можно вписать окружность и описать около него окружность.
23) Центры вписанной и описанной окружности треугольника не являются замечательными точками.
Ключ:
«+»: 1; 3; 4; 5; 6; 7; 9; 11; 13; 14; 17; 19; 20;
«-»: 2; 8; 10; 12; 15; 16; 18; 21; 22; 23.
Оценки:
«3» - 11 – 14;
«4» - 15 – 21;
«5» - 22 - 23

 Получите свидетельство
Получите свидетельство Вход
Вход












 Тесты для проверки теоретический знаний по геометрии 8-9 класс (24.27 KB)
Тесты для проверки теоретический знаний по геометрии 8-9 класс (24.27 KB)
 0
0 1438
1438 88
88 Нравится
0
Нравится
0


