Тема 5.2.3 Виды векторов. Разложение вектора по базису.
Модуль вектора.
Виды векторов
Нуль – вектор – это вектор, начало и конец которого совпадают, его длина равна нулю, направления этот вектор не имеет (точка).
Единичный вектор – это вектор, длина которого равна одному.
Коллинеарные вектора ( 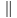 ) – это вектора, лежащие на параллельных прямых (на одной прямой). Среди коллинеарных векторов можно выделить:
) – это вектора, лежащие на параллельных прямых (на одной прямой). Среди коллинеарных векторов можно выделить:
 Сонаправленные вектора (
Сонаправленные вектора (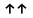 ) – это коллинеарные вектора, имеющие одинаковое направление.
) – это коллинеарные вектора, имеющие одинаковое направление.
Противоположнонаправленные вектора (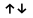 ) – это коллинеарные вектора, имеющие разное направление.
) – это коллинеарные вектора, имеющие разное направление.
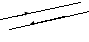
Равные вектора – это сонаправленные вектора, имеющие равную длину.
 Ортогональные вектора (
Ортогональные вектора (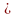 ) – это вектора, лежащие на перпендикулярных прямых.
) – это вектора, лежащие на перпендикулярных прямых.
Среди ортогональных векторов можно выделить:
ортонормированные вектора – это ортогональные вектора, длина которых равна одному;
орты – это ортонормированные вектора 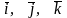 , лежащие на осях координат. Причем, если вектор задан своими координатами, т.е.
, лежащие на осях координат. Причем, если вектор задан своими координатами, т.е. 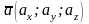 , то его можно записать в ортах следующим образом:
, то его можно записать в ортах следующим образом: 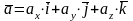 .
.
Компланарные вектора – это вектора, лежащие в параллельных плоскостях (в одной плоскости).
Зная координаты вектора, можно найти его длину, как корень квадратный из суммы квадратов его координат, т.е. если 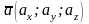 , то
, то 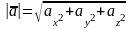 . Например, если
. Например, если 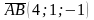 , то
, то 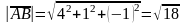 .
.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Тема 5.2.3 Виды векторов (51.86 KB)
Тема 5.2.3 Виды векторов (51.86 KB)
 0
0 239
239 18
18 Нравится
0
Нравится
0






