Технологическая карта открытого урока по геометрии
Класс: 9
| Тема урока | Теорема синусов и косинусов | |||||||||||||
| Тип урока | Урок «открытия новых знаний» | |||||||||||||
| Цели деятельности учителя | Создать условия для доказательства теоремы синусов; способствовать развитию умения применять теоремы синусов при решении задач | |||||||||||||
| Термины и понятия | Синус, косинус, треугольник, площадь треугольника, пропорция | |||||||||||||
| Планируемые результаты | ||||||||||||||
| Предметные умения | Универсальные учебные действия | |||||||||||||
| Умеют применять определение синуса и косинуса для доказательства теоремы | Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют видеть математическую задачу в контексте Регулятивные: осознают и принимают учебные задачи. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем; участвуют в диалоге. Личностные: владеют коммуникативной компетентностью | |||||||||||||
| Организация пространства | ||||||||||||||
| Формы работы | Фронтальная (Ф); индивидуальная (И) | |||||||||||||
| Образовательные ресурсы | • Задания для самостоятельной работы; презентация; буклет. | |||||||||||||
| I этап. Организационный момент | ||||||||||||||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | ||||||||||||
| Создать благоприятный настрой на работу | (Ф/И) Приветствует учащихся, проверяет готовность рабочего места учащихся к учебному занятию, создает настрой на работу Здравствуйте, я рада вас видеть. Эпиграф «Три пути ведут к знанию: путь размышления - это путь самый благородный. Путь подражания – Самый Легкий, Путь опыта – самый горький. Притча: Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: “Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая?” А сам думает: “Скажет живая – я ее умерщвлю, скажет мертвая – выпущу”. Мудрец, подумав, ответил: “Все в твоих руках”.
– Чем мы занимались на прошлом уроке? – Какие задачи вы учились решать? Сегодня на уроке мы продолжим работать с треугольником и расширим свои знания о нем.Я уверена, что на этом уроке мы с вами будем так же дружно и успешно работать, как и на предыдущих занятиях.Желаю вам новых открытий и успешных ответов. | Приветствуют учителя. Включаются в деловой ритм урока.
Отвечают на вопросы учителя.
- Доказали теорему о площади треугольника. - Задачи на вычисление площади треугольника по двум сторонам и углу между ними.
| ||||||||||||
| II этап. Актуализация опорных знаний | ||||||||||||||
| Цельдеятельности | Деятельность учителя | Деятельность учащихся | ||||||||||||
| Установить правильностьдомашнего задания; выявить и устранить в ходе проверки обнаруженные пробелы. Проверить уровень сформированности теоретических знаний | (Ф/И) Проверка домашнего задания Приступим к проверке ДЗ: № 1020(в) – Как вы определили значение синуса угла 48 градусов? № 102.
2. Фронтальный опрос: - Какие элементы треугольника вы знаете? -Что значит «решить треугольник»? - Сформулируйте теорему о площади треугольника?
-Какие формулы для вычисления площади треугольника вы знаете?
- Что такое пропорция? - Сформулируйте основное свойство пропорции? - Сформулируйте определение sinα, cosα, tgα острых углов прямоугольного треугольника.
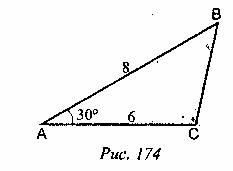
3. Решение задач по готовым чертежам 1) Найдите площадь треугольника АВС.
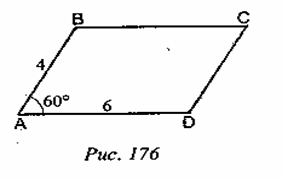
2) Найдите площадь параллелограмма АВСD.
| Задают вопросы по ДЗ. Комментируют решение задач. Отвечают на вопросы учителя. - S= ½∙14∙7∙sin48°=7∙7∙0,7347=36,41 (см2) -Пользуясь таблицей Брадиса, с помощью калькулятора… Комментируют решение задачи: (
Отвечают на вопросы учителя. - Вершины, стороны, углы. - Решить треугольник»- это значит найти все его элементы.
- Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
-Формулы для вычисления площади треугольника:
- Пропорция - это равенство отношений. - Произведение крайних членов равно произведению средних членов. -Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. - Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе. - Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему. Решают задачи по готовым чертежам (устно)
1)12
2)12 | ||||||||||||
| III этап.Создание проблемной ситуации | ||||||||||||||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | ||||||||||||
| Осуществить вход на тему урока и цель урока. | (Ф/И) 1) Предлагается решить устно задачу.
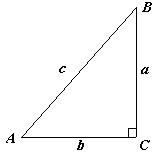
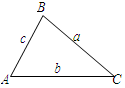
- Верно ли для прямоугольного треугольника равенство:
-Сделайте вывод? -А как вы думаете, верно ли это утверждение для любого треугольника?». Сегодня нам предстоит ответить на этот вопрос.
– Найдите отношения сторон ВС, АВ, АС к синусам противоположных углов. – Что вам придется доказывать? – Как называется утверждение, которое требуется доказать? - Какая функция присутствует в отношениях? - Значит тема нашего урока…? (Согласованная тема записывается в тетрадях - «Теорема синусов»). - Какова цель нашего урока? - Аещёкакова цель нашего урока? | Решают задачу (устно), делают вывод.
Вывод: В прямоугольном треугольнике стороны пропорциональны синусам противолежащих углов Высказывают предположения…..
Ответы учащихся….. -
- Равенство отношений
- Теорема
- Синус
-Теорема синусов
Записывают тему урока в тетради
- Доказать теорему синусов. - Научится применять теорему при решении задач. | ||||||||||||
| VI этап. Изучение нового материала | ||||||||||||||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | ||||||||||||
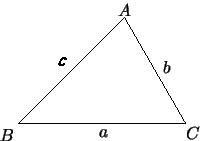
| Доказать теорему синусов | (Ф) - Попытайтесь сформулировать теорему. Теорема.Стороны треугольника пропорциональны синусам противолежащих углов. ( Доказательство проводится в виде беседы учителя с учащимися)
Дано: Пусть в Доказать: Доказательство. По теореме о площади треугольника
Из первых двух равенств получаем Мы узнали, что отношения сторон к синусам противолежащих им углов равны между собой, но чему же именно равны эти отношения? Чтобы ответить на этот вопрос, обратимся к задаче №1033. Таким образом, мы получили дополнительное правило отыскания радиуса описанной около треугольника окружности. В заданиях ОГЭ тоже встречается теорема синусов. Я для вас приготовила буклет «Теорема синусов и теорема косинусов в ОГЭ». Ваша задача с ним дома ознакомиться и решить дополнительные задачи.. Раздаёт буклеты. | Формулируют теорему. Принимают участие в беседе при доказательстве теоремы. Записывают теорему и её доказательство. Находят ответ на вопрос, делают вывод. Вывод: если в треугольнике против сторон a, b, c лежат углы α, β, γ соответственно, то где R – радиус окружности, описанной около треугольника.
| ||||||||||||
| VI этап. Физминутка | ||||||||||||||
| VII этап. этап. Закрепление изученного материала | ||||||||||||||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | ||||||||||||
| Показать применение теоремы при решении задач | (Ф/И) Проверяет и контролирует работу учащихся 1. Запишите теорему синусов для ∆МKЕ. 3. На доске и в тетрадях решить № 1025 (а)
| Записывают теорему синусов для ∆МKЕ. Работает один учащийся у доски, остальные в тетрадях по учебнику. № 1025. а) У доски решает-Тычинина Валерия
а) А = 60°, В = 40°, с = 14. С = 180° – (А + В) = 80°. По теореме синусов:
| ||||||||||||
| VIII этап. этап. Самостоятельная работа | ||||||||||||||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | ||||||||||||
| Обеспечить выполнение учащимися самостоятельной работы и взаимопроверку | Проводит самостоятельнуюработу с взаимопроверкойпо эталону Самостоятельная работа с взаимопроверкой по эталону. Вариант 1 Определите, каким – остроугольным, прямоугольным или тупоугольным – является треугольник, два угла которого равны 43° и 48°. Какие из следующих утверждений верны? Стороны треугольника пропорциональны синусам противолежащих углов Стороны треугольника пропорциональны косинусам противолежащих углов Стороны треугольника пропорциональны синусам прилежащих углов Стороны треугольника пропорциональны противолежащим углам Установите соответствие?
Выразите х и учерез синусы острых углов.
Вариант 2 1. Определите, каким – остроугольным, прямоугольным или тупоугольным – является треугольник, два угла которого равны 35° и 56°. 2.Какие из следующих утверждений верны? 1.Стороны треугольника пропорциональны синусам противолежащих углов 2.Стороны треугольника пропорциональны косинусам противолежащих углов 3.Стороны треугольника пропорциональны синусам прилежащих углов 4.Стороны треугольника пропорциональны противолежащим углам Установите соответствие?
Выразите х и учерез синусы острых углов. | Выполняют самостоятельную работу по вариантам. Обмениваются тетрадями и взаимопроверкуработ по эталону Ответы: Вариант 1 1. Остроугольным 2. 1 3.1-Б, 2-В, 3-А 4. Решение: Ответ: Вариант 2 1.Остроугольным 2. 1 3. 1-Б, 2-В, 3-А 4. Решение: Ответ: | ||||||||||||
| IX этап.Домашние задание | ||||||||||||||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | ||||||||||||
| Нацелить | Формулирует домашнее задание -Откройте дневники, запишите ДЗ:выучить п. 101, 102; решить № 1025 (б, д, ж), доказать теорему косинусов, разобрать задачи и решить задачи из буклета. -Закройте дневники. | (И) Записывают домашнее задание в дневники | ||||||||||||
| Xэтап.Итоги урока. Рефлексия | ||||||||||||||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | ||||||||||||
| Зафиксировать содержание урока;организовать рефлексию и самооценку учениками собственной учебной деятельности | (Ф/И)Задает вопросы: – Какую цель мы ставили перед собой на уроке? – Мы достигли поставленной цели? – Проанализируйте свою работу на уроке: 1. Сегодня на уроке я……… 2.Я знаю……. 3. У меня хорошо получилось………. 4.В самостоятельной работе у меня ……….. 5.Я своей работой на уроке……………… Выставляет оценки за урок Наш урок я хочу закончить словами персидско-таджикского поэта Рудаки: «С тех пор как существует мирозданье, Такого нет, кто б не нуждался в знанье. Какой мы ни возьмем язык и век, Всегда стремится к знанью человек » Спасибо за урок. До свидания! | Отвечают на вопросы учителя Заполняют карточку рефлексии
| ||||||||||||
Вариант 1
1.Определите, каким – остроугольным, прямоугольным или тупоугольным – является треугольник, два угла которого равны 43° и 48°.
2.Какие из следующих утверждений верны?
1.Стороны треугольника пропорциональны синусам противолежащих углов
2.Стороны треугольника пропорциональны косинусам противолежащих углов
3.Стороны треугольника пропорциональны синусам прилежащих углов
4.Стороны треугольника пропорциональны противолежащим углам
3.Установите соответствие?
| 1. 2. 3. | А) теорема Пифагора Б) теорема синусов В) формула Герона |
4.Выразите х и учерез синусы острых углов.
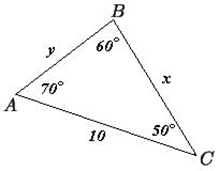
Вариант 2
1. Определите, каким – остроугольным, прямоугольным или тупоугольным – является треугольник, два угла которого равны 35° и 56°.
2.Какие из следующих утверждений верны?
1.Стороны треугольника пропорциональны синусам противолежащих углов
2.Стороны треугольника пропорциональны косинусам противолежащих углов
3.Стороны треугольника пропорциональны синусам прилежащих углов
4.Стороны треугольника пропорциональны противолежащим углам
Установите соответствие?
| 1. 2. 3. | А) теорема Пифагора Б) теорема синусов В) формула Герона |
Выразите х и учерез синусы острых углов.
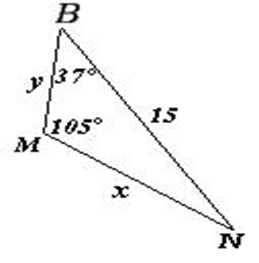

 Получите свидетельство
Получите свидетельство Вход
Вход





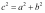









 Технологическая карта урока по геометрии (449.18 KB)
Технологическая карта урока по геометрии (449.18 KB)
 0
0 2
2 0
0 Нравится
0
Нравится
0


