ПЛАНИМЕТРИЯ
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Свойства и признаки параллельных прямых
Аксиома параллельных. Через данную точку можно провести не более одной прямой, параллельной данной.
Если две прямые параллельны одной и той же прямой, то они параллельны между собой.
Две прямые, перпендикулярные одной и той же прямой, параллельны.
Если две параллельные прямые пересечь третьей, то образованные при этом: внутренние накрест лежащие углы равны; соответственные углы равны; внутренние односторонние углы в сумме составляют 180°.
Если при пересечении двух прямых третьей образуются равные внутренние накрест лежащие углы, то прямые параллельны.
Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Теорема Фалеса. Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие вторую сторону угла, то на второй стороне угла отложатся также равные отрезки.
Теорема о пропорциональных отрезках. Параллельные прямые пересекающие стороны угла, высекают на них пропорциональные отрезки.
ТРЕУГОЛЬНИК
Признаки равенства треугольников
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то треугольники равны.
Признаки равенства прямоугольных треугольников
По двум катетам.
По катету и гипотенузе.
По гипотенузе и острому углу.
По катету и острому углу.
Теорема о сумме углов треугольника и следствия из неё
Сумма внутренних углов треугольника равна 180°.
Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.
Сумма внутренних углов выпуклого n-угольника равна 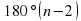 .
.
Сумма внешних углов n-угольника равна 360°.
Углы со взаимно перпендикулярными сторонами равны, если они острые или оба тупые.
Угол между биссектрисами смежных углов равен 90°.
Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.
Основные свойства и признаки равнобедренного треугольника
Углы при основании равнобедренного треугольника равны.
Если два угла треугольника равны, то он равнобедренный.
В равнобедренном треугольнике медиана, биссектриса и высота, проведенные к основанию, совпадают.
Если в треугольнике совпадает любая пара отрезков из тройки: медиана, биссектриса, высота, то он является равнобедренным.
Неравенство треугольника и следствия из него
Сумма двух сторон треугольника больше его третьей стороны.
Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.
Против большего угла треугольника лежит большая сторона.
Против большей стороны треугольника лежит больший угол.
Гипотенуза прямоугольного треугольника больше катета.
Если из одной точки проведены к прямой перпендикуляр и наклонные, то
перпендикуляр короче наклонных;
большей наклонной соответствует большая проекция и наоборот
Средняя линия треугольника. Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Теорема о средней линии треугольника. Средняя линия треугольника параллельна стороне треугольника и равна ее половине.
Теоремы о медианах треугольника
Медианы треугольника пересекаются в одной точке и делятся отношении 2 : 1, считая от вершины.
Если медиана треугольника равна половине стороны, к которой проведена, то треугольник прямоугольный.
Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Свойство серединных перпендикуляров к сторонам треугольника. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.
Теорема о высотах треугольника. Прямые, содержащие высоты треугольника, пересекаются в одной точке.
Теорема о биссектрисах треугольника. Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.
Свойство биссектрисы треугольника. Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
Признаки подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, равны, то треугольники подобны.
Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то треугольники подобны.
Площади подобных треугольников
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Если два треугольника имеют равные углы, то их площади относятся как произведение сторон, заключающих эти углы.
В прямоугольном треугольнике
Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла.
Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к этому катету острого угла.
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30°.
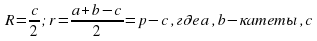 – гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружности соответственно.
– гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружности соответственно.
Теорема Пифагора и теорема, обратная теореме Пифагора
Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный.
Средние пропорциональные в прямоугольном треугольнике.
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу.
Метрические соотношения в треугольнике
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон косинус угла между ними.
Следствие из теоремы косинусов. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
Формула для медианы треугольника. Если m — медиана треугольника, проведенная к стороне с, то 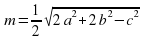 , где a и b - остальные стороны треугольника.
, где a и b - остальные стороны треугольника.
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.
Обобщённая теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.
Формулы площади треугольника
Площадь треугольника равна половине произведения основания на высоту.
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
Площадь треугольника равна произведению трёх его сторон, деленному на учетверённый радиус описанной окружности.
Формула Герона: 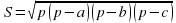 , где р — полупериметр; а,b,с — стороны треугольника.
, где р — полупериметр; а,b,с — стороны треугольника.
Элементы равностороннего треугольника. Пусть h, S,r , R - высота, площадь, радиусы вписанной и описанной окружностей равностороннего треугольника со стороной а. Тогда
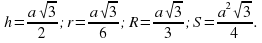
ЧЕТЫРЕХУГОЛЬНИК
Параллелограмм. Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма.
Диагональ разбивает параллелограмм на два равных треугольника.
Противоположные стороны параллелограмма попарно равны.
Противоположные углы параллелограмма попарно равны.
Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.
Свойство середин сторон четырёхугольника. Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.
Прямоугольник. Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника.
Диагонали прямоугольника равны.
Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник.
Квадрат. Квадратом называется прямоугольник, все стороны которого равны.
Ромб. Ромбом называется четырёхугольник, все стороны которого равны.
Свойства и признаки ромба.
Диагонали ромба перпендикулярны.
Диагонали ромба делят его углы пополам.
Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
Трапеция. Трапецией называется четырёхугольник, у которого только противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Отрезок, соединяющий середины диагоналей трапеции, равен полусумме оснований.
Замечательное свойство трапеции. Точка пересечения диагоналей и, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Равнобедренная трапеция. Трапеция называется равнобедренной, если ее боковые стороны равны.
Свойства и признаки равнобедренной трапеции.
Углы при основании равнобедренной трапеции равны.
Диагонали равнобедренной трапеции равны.
Если углы при основании трапеции равны, то она равнобедренная.
Если диагонали трапеции равны, то она равнобедренная.
Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.
Формулы площади четырёхугольника
Площадь параллелограмма равна произведению основания на высоту.
Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
Площадь прямоугольника равна произведению двух его соседних сторон.
Площадь ромба равна половине произведения его диагоналей.
Площадь трапеции равна произведению полусуммы основании на высоту.
Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
Формула Герона для четырёхугольника, около которого можно описать окружность: 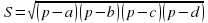 , где a,b,c,d - стороны этого четырёхугольника, р — полупериметр, a S — площадь.
, где a,b,c,d - стороны этого четырёхугольника, р — полупериметр, a S — площадь.
Подобные фигуры
Отношение соответствующих линейных элементов подобных фигур равно коэффициенту подобия.
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Правильный многоугольник.
Пусть ап — сторона правильного n-угольника, а 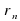 и Rn — радиусы вписанной и описанной окружностей. Тогда:
и Rn — радиусы вписанной и описанной окружностей. Тогда:
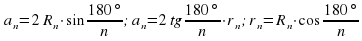 .
.
Окружность.
Окружностью называется геометрическое место точек плоскости, удаленных от данной точки, называемой центром окружности, на одно и то же положительное расстояние.
Основные свойства окружности
Диаметр, перпендикулярный хорде, делит хорду и стягиваемые ею дуги полам.
Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
Серединный перпендикуляр к хорде проходит через центр окружности.
Равные хорды удалены от центра окружности на равные расстояния.
Хорды окружности, удалённые от центра на равные расстояния, равны.
Окружность симметрична относительно любого своего диаметра.
Дуги окружности, заключенные между параллельными хордами, равны.
Из двух хорд больше та, которая менее удалена от центра.
Диаметр есть наибольшая хорда окружности.
Замечательные свойства окружности
Геометрическое место точек М, из которых отрезок АВ виден под прямым углом (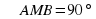 ), есть окружность с диаметром АВ без точек А и В.
), есть окружность с диаметром АВ без точек А и В.
Геометрическое место точек М, из которых отрезок АВ виден под острым углом {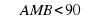 °), есть внешность круга с диаметром АВ без точек прямой АВ.
°), есть внешность круга с диаметром АВ без точек прямой АВ.
Геометрическое место точек М, из которых отрезок АВ виден под тупым углом 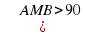 °), есть внутренность круга с диаметром АВ без точек отрезка АВ.
°), есть внутренность круга с диаметром АВ без точек отрезка АВ.
Геометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги равных окружностей (без концов этих дуг).
Касательная к окружности. Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности.
Касательная перпендикулярна радиусу, проведённому в точку касания.
Если прямая а, проходящая через точку на окружности, перпендикулярна радиусу, проведённому в эту точку, то прямая а — касательная к окружности.
Если прямые, проходящие через точку М, касаются окружности в точках А и В, то MA = MB и  AMO =
AMO =  BMO, где точка О – центр окружности.
BMO, где точка О – центр окружности.
Центр окружности, вписанной в угол, лежит на биссектрисе угла.
Касающиеся окружности. Говорят, что две окружности касаются, если они имеют единственную общую точку (точку касания).
Точка касания двух окружностей лежит на их линии центров.
Окружности радиусов r и R с центрами 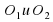 касаются внешним образом тогда и только тогда, когда
касаются внешним образом тогда и только тогда, когда 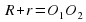 .
.
Окружности радиусов r и R (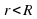 ) с центрами
) с центрами 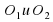 касаются внутренним образом тогда и только тогда, когда
касаются внутренним образом тогда и только тогда, когда 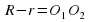 .
.
Окружности с центрами 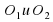 касаются внешним образом в точке К. Некоторая прямая касается этих окружностей в различных точках А и В и пересекается с общей касательной, проходящей через точку К, в точке С. Тогда
касаются внешним образом в точке К. Некоторая прямая касается этих окружностей в различных точках А и В и пересекается с общей касательной, проходящей через точку К, в точке С. Тогда 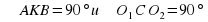 .
.
Отрезок общей внешней касательной к двум касающимся окружностям радиусов r и R равен отрезку общей внутренней касательной, заключённому между общими внешними. Оба эти отрезка равны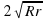 .
.
Углы, связанные с окружностью
Величина дуги окружности равна величине центрального угла, на неё опирающегося.
Вписанный угол равен половине угловой величины дуги, на которую он опирается.
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
Угол между двумя секущими, пересекающимися вне круга, равен полуразности дуг, высекаемых секущими на окружности.
Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними.
Свойства хорд окружности
Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде.
Произведения длин отрезков хорд АВ и CD окружности, пересекающихся в точке Е, равны, то есть 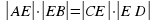 .
.
Вписанные и описанные окружности
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Центр окружности, описанной около прямоугольного треугольника - середина гипотенузы.
Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны.
Если четырёхугольник можно вписать в окружность, то сумма его противоположных углов равна 180°.
Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.
Если в трапецию можно вписать окружность, то боковая сторона трапеции видна из центра окружности под прямым углом.
Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону.
Если в многоугольник можно вписать окружность, то его площадь равна произведению полупериметра многоугольника на радиус этой окружности.
Теорема о касательной и секущей и следствие из неё
Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на ее внешнюю часть равно квадрату касательной.
Произведение всей секущей на её внешнюю часть для данной точки и данной окружности постоянно.
Длина окружности радиуса R равна 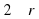 .
.
Площадь круга радиуса R равна 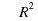 .
.
СТЕРЕОМЕТРИЯ
Аксиомы стереометрии
Основные аксиомы
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Факты, непосредственно связанные с аксиомами
Через прямую и точку, не лежащую на этой прямой, проходит единственная плоскость.
Через две параллельные прямые проходит единственная плоскость.
Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.
Параллельность в пространстве
Признак параллельности прямой и плоскости. Если прямая а параллельна некоторой прямой плоскости  , то прямая а параллельна плоскости
, то прямая а параллельна плоскости  .
.
Если через прямую а, параллельную плоскости  , провести плоскость, пересекающую плоскость
, провести плоскость, пересекающую плоскость  по прямой b, то прямые a и b параллельны.
по прямой b, то прямые a и b параллельны.
Если прямые a и b параллельны, а плоскость, проходящая через прямую а, пересекается с плоскостью, проходящей через прямую b, то прямая пересечения плоскостей параллельна прямым a и b.
Транзитивность параллельности прямых в пространстве. Если прямая а параллельна прямой b, а прямая b параллельна прямой с, то прямая а параллельна прямой с.
Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.
Если две параллельные плоскости пересечены третьей, то прямые пересечения параллельны.
Транзитивность параллельности плоскостей. Если плоскость  параллельна плоскости
параллельна плоскости  , а плоскость
, а плоскость  параллельна плоскости
параллельна плоскости  , то плоскость
, то плоскость  параллельна плоскости
параллельна плоскости  .
.
Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.
Через точку, не лежащую в плоскости, проходит единственная плоскость, параллельная данной.
Скрещивающиеся прямые
Признак скрещивающихся прямых. Если прямая a лежит в плоскости  , а прямая b пересекает эту плоскость в точке, не лежащей на прямой а, то а и b — скрещивающиеся прямые.
, а прямая b пересекает эту плоскость в точке, не лежащей на прямой а, то а и b — скрещивающиеся прямые.
Через две скрещивающиеся прямые проходит единственная пара параллельных плоскостей.
Геометрическое место середин отрезков с концами на двух скрещивающихся прямых есть плоскость, параллельная этим прямым и проходящая через середину одного из таких отрезков.
Угол между скрещивающимися прямыми (угол между пересекающимися в произвольной точке М прямыми, соответственно параллельными данным) не зависит от выбора точки М.
Для любых двух скрещивающихся прямых существует единственный общий перпендикуляр (отрезок с концами на этих прямых, перпендикулярный обеим прямым).
Параллельное проектирование
Прямая, непараллельная проектирующей, переходит в прямую.
Пара параллельных прямых, непараллельных проектирующей, переходит в пару параллельных прямых или в одну прямую.
При проектировании сохраняется отношение отрезков, лежащих на одной прямой или на параллельных прямых.
Наклонная пересекает плоскость в точке, лежащей на любой её параллельной проекции на эту плоскость.
Площадь ортогональной проекции плоского многоугольника на плоскость равна произведению площади проектируемого многоугольник на косинус угла между плоскостью этого многоугольника и плоскостью проекций.
Координаты и векторы в пространстве
Координаты вектора равны разностям соответствующих координат конца и начала данного вектора.
Для того чтобы векторы  были коллинеарны, необходимо и достаточно, чтобы выполнялось равенство
были коллинеарны, необходимо и достаточно, чтобы выполнялось равенство  , где k — некоторое число.
, где k — некоторое число.
Для того чтобы три вектора были компланарны, необходимо и достаточно чтобы один из них можно было представить в виде линейной комбинации двух других ( , где х, у — некоторые числа).
, где х, у — некоторые числа).
Любой вектор можно единственным образом разложить по трём некомпланарным векторам.
Если М — середина АВ, то .
Если М — середина АВ, a N — середина CD, то .
Если М — точка пересечения медиан треугольника ABC, то .
Если М — точка пересечения диагоналей параллелограмма ABCD, то .
Координаты середины отрезка равны средним арифметическим координат его концов.
Свойства скалярного произведения векторов:
 ;
;
 ;
;
 ;
;
 ;
;
;
 , причем равенство достигается тогда и только тогда, когда векторы
, причем равенство достигается тогда и только тогда, когда векторы  коллинеарны;
коллинеарны;
тогда и только тогда, когда их скалярное произведение равно нулю.
Расстояние между точками  равно .
равно .
Угол между ненулевыми векторами. Если  — угол между ненулевыми векторами , то .
— угол между ненулевыми векторами , то .
Уравнение плоскости, проходящей через точку  перпендикулярно ненулевому вектору
перпендикулярно ненулевому вектору  (вектор нормали), имеет вид: /
(вектор нормали), имеет вид: /
Параметрические уравнения прямой, проходящей через точку  параллельно ненулевому вектору
параллельно ненулевому вектору  (направляющий вектор), имеют вид:
(направляющий вектор), имеют вид:
Уравнения прямой, проходящей через две точки  , имеют вид:
, имеют вид:  .
.
Прямая как пересечение двух плоскостей задается системой где  и
и  , а коэффициенты при соответствующих неизвестных непропорциональны.
, а коэффициенты при соответствующих неизвестных непропорциональны.
Угол между плоскостями. Если  — угол между плоскостями заданными уравнениями и , то .
— угол между плоскостями заданными уравнениями и , то .
Уравнение плоскости «в отрезках». Если плоскость пересекает оси координат в точках , то ее уравнение можно представить в виде  .
.
Расстояние от точки до плоскости. Если  - расстояние от точки
- расстояние от точки  до плоскости , то .
до плоскости , то .
Перпендикулярность прямой и плоскости
Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.
Если две прямые перпендикулярны одной плоскости, то они параллельны.
Если одна из двух параллельных прямых перпендикулярна плоскости, то прямая также перпендикулярна этой плоскости.
Две плоскости, перпендикулярные одной прямой, параллельны.
Если прямая и плоскость перпендикулярны одной прямой, то они параллельны.
Через данную точку проходит единственная плоскость, перпендикулярная данной прямой.
Через данную точку проходит единственная прямая, перпендикулярная данной плоскости.
Теорема о трех перпендикулярах. Прямая, лежащая в плоскости, перпендикулярна наклонной к плоскости тогда и только тогда, когда она перпендикулярна ортогональной проекции наклонной на эту плоскость.
Если из одной точки проведены к плоскости перпендикуляр и наклонные, то
перпендикуляр короче наклонных;
равные наклонные имеют равные ортогональные проекции;
большей наклонной соответствует большая ортогональная проекция;
из двух наклонных больше та, ортогональная проекция которой больше.
Теорема об угле прямой с плоскостью. Угол между наклонной и ее ортогональной проекцией на плоскость меньше угла между этой наклонной и любой другой прямой плоскости.
Геометрическое место точек, равноудалённых от концов отрезка, есть плоскость, перпендикулярная этому отрезку и проходящая через его середину.
Геометрическое место точек, удалённых на данное расстояние от данной плоскости, есть две параллельные плоскости.
Геометрическое место точек, равноудалённых от вершин треугольника, есть прямая, проходящая через центр описанной окружности треугольника перпендикулярно его плоскости.
Двугранный угол
Линейный угол двугранного угла (сечение двугранного угла плоскостью, перпендикулярной его ребру) не зависит от выбора точки на ребре двугранного угла.
Геометрическое место внутренних точек двугранного угла, равноудаленных от его граней, есть биссекторная плоскость двугранного угла.
Необходимое и достаточное условие перпендикулярности плоскостей. Две плоскости перпендикулярны (образуют прямой двугранный угол) тогда и только тогда, когда одна из них проходит через перпендикуляр к другой.
Если две пересекающиеся плоскости перпендикулярны третьей, то они пересекаются по прямой, также перпендикулярной этой плоскости.
Многогранные углы
Плоский угол трёхгранного угла меньше суммы двух других его плоских углов.
Сумма плоских углов выпуклого многогранного угла меньше  .
.
Сфера. Касательная плоскость. Касающиеся сферы
Сечение сферы плоскостью, удалённой от центра сферы на расстояние, меньшее радиуса, есть окружность. Основание перпендикуляра, опущенного из центра сферы на секущую плоскость, есть центр этой окружности.
Касательная плоскость к сфере (плоскость, имеющая со сферой единственную общую точку) перпендикулярна радиусу сферы, проведенному в точку касания.
Касательная прямая к сфере (прямая, имеющая со сферой единственную общую точку) перпендикулярна радиусу сферы, проведённому в точку касания.
Центр сферы, вписанной в двугранный угол, лежит в биссекторной плоскости этого угла.
Отрезки касательных прямых, проведённых к сфере из одной точки равны между собой.
Линия центров касающихся сфер (имеющих единственную общую точку) проходит через их точку касания.
Если две различные сферы имеют более одной общей точки, то они пересекаются по окружности. Плоскость этой окружности перпендикулярна линии центров данных сфер.
Пирамида
Правильная пирамида
Если  – правильная треугольная пирамида вершиной
– правильная треугольная пирамида вершиной  , высотой
, высотой  и стороной основания
и стороной основания  - середины сторон соответственно
- середины сторон соответственно  , то
, то
 - угол бокового угла с плоскостью основания;
- угол бокового угла с плоскостью основания;
 - линейный угол двугранного угла боковой грани с плоскостью основания;
- линейный угол двугранного угла боковой грани с плоскостью основания;
 (где
(где  - основание перпендикуляра, опущенного из вершины
- основание перпендикуляра, опущенного из вершины  основания на боковое ребро
основания на боковое ребро  ) – линейный угол между боковыми гранями пирамиды;
) – линейный угол между боковыми гранями пирамиды;
- высота треугольника основания;
- ортогональная проекция бокового ребра на плоскость основания;
 – общий перпендикуляр противоположных ребер
– общий перпендикуляр противоположных ребер  .
.
Противоположные ребра правильной треугольной пирамиды попарно перпендикулярны.
Высота правильного тетраэдра с ребром  равна
равна  .
.
Если  - правильная четырехугольная пирамида с вершиной
- правильная четырехугольная пирамида с вершиной  , высотой
, высотой  и стороной основания
и стороной основания  , а
, а  – середины сторон соответственно
– середины сторон соответственно  , то
, то
- угол бокового ребра c плоскостью основания;
– линейный угол двугранного угла боковой грани с плоскостью основания;
 (где
(где  - основание перпендикуляра, опущенного из основания
- основание перпендикуляра, опущенного из основания  основания на боковое ребро
основания на боковое ребро  ) – линейный угол между соседними боковыми гранями пирамиды;
) – линейный угол между соседними боковыми гранями пирамиды;
 линейный угол двугранного угла между противоположными боковыми гранями;
линейный угол двугранного угла между противоположными боковыми гранями;
- ортогональная проекция бокового ребра на плоскость основания;
- ортогональная проекция апофемы на плоскость основания;
FM – общий перпендикуляр диагонали  основания и скрещивающегося с ней бокового ребра
основания и скрещивающегося с ней бокового ребра  ю
ю
Боковое ребро правильной четырехугольной пирамиды перпендикулярно скрещивающейся с ним диагонали основания.
Правильный тетраэдр. Пусть  -ребро правильного тетраэдра, а
-ребро правильного тетраэдра, а  и
и  - радиусы описанной и вписанной сфер,
- радиусы описанной и вписанной сфер,  - бьем тетраэдра. Тога: .
- бьем тетраэдра. Тога: .
Пирамида
Если боковые грани треугольной пирамиды образуют равные двугранные углы с плоскостью основания, то высота пирамиды проходит либо через центр вписанной окружности, либо через центр одной из вневписанных окружностей основания.
Если все боковые рёбра пирамиды образуют с основанием равные углы или если все боковые рёбра равны, то высота пирамиды проходит через центр окружности, описанной около основания.
Теорема о медианах тетраэдра. Медианы тетраэдра (отрезки, соединяющие вершины тетраэдра с точками пересечения медиан противолежащих граней) пересекаются в одной точке и делятся ею в отношении 3:1, считая от вершины.
Если пересечь пирамиду плоскостью, параллельной основанию, то в сечении образуется многоугольник, подобный основанию.
В пирамиде и в конусе площади сечений, параллельных основанию, относятся как квадраты их расстояний до вершины.
Параллелепипед
Параллелепипед называется прямым, если его боковые рёбра перпендикулярны основанию.
Прямой параллелепипед, в основании которого лежит прямоугольник, называется прямоугольным.
Свойства диагоналей прямоугольного параллелепипеда:
диагонали прямоугольного параллелепипеда равны.
квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений (длин трёх рёбер с общей вершиной).
Свойства граней и диагоналей параллелепипеда. Противоположные грани параллелепипеда равны и параллельны. Диагонали параллелепипеда пересекаются и делятся точкой пересечения пополам.
Диагональ  параллелепипеда
параллелепипеда  проходит через точку пересечения медиан треугольника
проходит через точку пересечения медиан треугольника  и делится ею в отношении
и делится ею в отношении  считая от точки A.
считая от точки A.
Площади поверхности многогранников
Площадь боковой поверхности призмы равна произведению периметра перпендикулярного сечения призмы на боковое ребро.
Площадь боковой поверхности правильной пирамиды равна площади ее основания, делённой на косинус угла боковой грани с плоскостью основания.
Объемы многогранников
Объём прямоугольного параллелепипеда равен произведению трёх его измерений.
Объём наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.
Объём призмы равен произведению площади основания на высоту.
Объём треугольной призмы равен половине произведения площади боковой грани на расстояние между этой гранью и противолежащим ей боковым ребром.
Объём пирамиды равен трети произведения площади основания на высоту.
Пирамиды с равными высотами и равновеликими основаниями равновелики.
Плоскость, проходящая через вершину пирамиды и прямую, лежащую в основании, делит объем пирамиды в том же отношении, в котором прямая делит площадь основания.
Если точки  лежат на боковых ребрах соответственно
лежат на боковых ребрах соответственно  треугольной пирамиды
треугольной пирамиды  или на их продолжениях, то оббьем пирамиды
или на их продолжениях, то оббьем пирамиды  относится к объему пирамиды
относится к объему пирамиды  как произведение отношений
как произведение отношений  .
.
Отношение объёмов подобных многогранников равно кубу коэффициента подобия.
Объём тетраэдра V равен шестой части произведения длин двух противоположных рёбер а и  на расстояние между ними
на расстояние между ними  и на синус угла
и на синус угла  между ними, то есть .
между ними, то есть .
Объём тетраэдра V равен двум третям произведения площадей двух граней Р и Q на синус угла  между ними, делённому на их общее ребро
между ними, делённому на их общее ребро  , то есть .
, то есть .
Объём тетраэдра равен трети произведения его полной поверхности на радиус вписанной сферы.
Объём многогранника, в который можно вписать сферу, равен трети произведения полной поверхности многогранника на радиус вписанной сферы.
 .
.
 Получите свидетельство
Получите свидетельство Вход
Вход


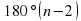 .
.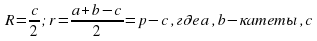 – гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружности соответственно.
– гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружности соответственно.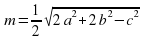 , где a и b - остальные стороны треугольника.
, где a и b - остальные стороны треугольника.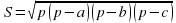 , где р — полупериметр; а,b,с — стороны треугольника.
, где р — полупериметр; а,b,с — стороны треугольника.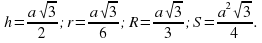
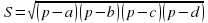 , где a,b,c,d - стороны этого четырёхугольника, р — полупериметр, a S — площадь.
, где a,b,c,d - стороны этого четырёхугольника, р — полупериметр, a S — площадь.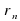 и Rn — радиусы вписанной и описанной окружностей. Тогда:
и Rn — радиусы вписанной и описанной окружностей. Тогда: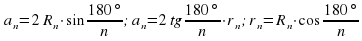 .
.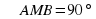 ), есть окружность с диаметром АВ без точек А и В.
), есть окружность с диаметром АВ без точек А и В.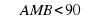 °), есть внешность круга с диаметром АВ без точек прямой АВ.
°), есть внешность круга с диаметром АВ без точек прямой АВ.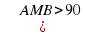 °), есть внутренность круга с диаметром АВ без точек отрезка АВ.
°), есть внутренность круга с диаметром АВ без точек отрезка АВ. AMO =
AMO = 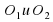 касаются внешним образом тогда и только тогда, когда
касаются внешним образом тогда и только тогда, когда 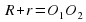 .
.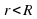 ) с центрами
) с центрами 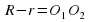 .
.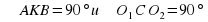 .
.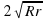 .
.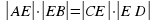 .
.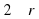 .
. 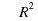 .
. , то прямая а параллельна плоскости
, то прямая а параллельна плоскости 








 Теоретический материал по планиметрии и стереометрии (58.29 КB)
Теоретический материал по планиметрии и стереометрии (58.29 КB)
 0
0 1410
1410 155
155 Нравится
0
Нравится
0









