Теорема косинусов — одна из теорем геометрии, гласит: Квадрат любой стороны треугольника (a) равен сумме квадратов двух других сторон треугольника (b и c), минус удвоенное произведение этих сторон на косинус угла (α) между ними. a2 = b2 + c2 − 2bccosα.
Доказательство. Рассмотрим треугольник ABC. Из вершины C на сторону AB опущена высота CD. Из треугольника ADC следует: AD = bcosα, DB = c − bcosα. Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений (1) и (2) и: b2 − (bcosα) 2 = a2 − (c − bcosα) 2 или a2 = b2 + c2 − 2bccosα.
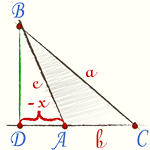
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному. Выражения для сторон b и c: b2 = a2 + c2 − 2accosβ c2 = a2 + b2 − 2abcosγ.
Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.
Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:

a2 = b2 + c2 – 2bc cosα.
Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Следствие из теоремы косинусов.
Теорема косинусов используется для определения cos угла треугольника...
Если конкретно:
Когда b2 + c2 - a2 > 0, угол α будет острым;
Когда b2 + c2 - a2 = 0, угол α будет прямым (когда угол α является прямым, значит, теорема косинусов переходит в теорему Пифагора) ;
Когда b2 + c2 - a2 < 0, угол α будет тупым.
Классическое доказательство теоремы косинусов.
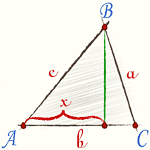
Пусть есть треугольник ABC. Из вершины C на сторону AB опустили высоту CD. Значит:
AD = b cos α,
DB = c – b cos α
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


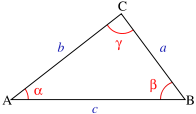 Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:
Для плоского треугольника, у которого стороны a, b, c и угол α, который противолежит стороне a, справедливо соотношение:










 Теорема косинусов (методический материал) (51.21 КB)
Теорема косинусов (методический материал) (51.21 КB)
 0
0 755
755 65
65 Нравится
0
Нравится
0



