УРОК ПО ТЕМЕ: «СУММА УГЛОВ ТРЕУГОЛЬНИКА»
Цели урока:
Образовательные: доказать теорему о сумме углов треугольника и учится применять её для решения задач;
Развивающие: развивать логическое мышление и навыки исследовательской работы;
Воспитательные: воспитывать сотрудничество, культуру умственного труда, интерес к изучению математики, расширение кругозора.
Универсальные учебные действия:
Коммуникативные:
планирование и организация учебного сотрудничества с учителем и сверстниками
умение вступать в диалог, участвовать в коллективном обсуждении вопроса
уметь оформлять свои мысли в устной форме; слушать и понимать речь других.
Регулятивные:
организация своей учебной деятельности
оценивание собственной деятельности на уроке
умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы
планирование своей деятельности для решения поставленной задачи и контроль полученного результата.
целеполагание.
Личностные:
мотивация учения
самоопределение.
формирование готовности к самообразованию
формирование позитивной самооценки
Познавательные:
структурирование собственных знаний по теме «Параллельность прямых»
формирование интереса к данной теме
умение осознанно и произвольно строить речевое высказывание в устной форме.
Тип учебного занятия: урок освоение нового материала.
Формы работы на уроке: практическая групповая работа, фронтальный опрос, научный эксперимент.
Методы: словесные, практические и проблемно-поисковые.
Педагогическая технология: проблемно-диалогическое обучение.
Оборудование: компьютер, мультимедийный проектор, презентация, модели треугольников, карточки.
Данный урок является первым в главе "Соотношения между сторонами и углами треугольника", опирается на знание учащимися признаков и свойств параллельных прямых, аксиомы параллельности. Урок готовит базу для решения задач, доказательства теорем о соотношении сторон и углов треугольника.
План урока:
Организационный момент.
Повторение
Устная работа.
Постановка проблемы, определение путей ее решения.
Выдвижение гипотезы.
Подтверждения гипотезы.
Доказательство теоремы.
Решение заданий на закрепление изученной теоремы.
Подведение итогов урока (рефлексия), задание на дом.
ХОД УРОКА
1. Организационный момент.
Сегодня наш класс превратится в научно-исследовательский институт, а вы станете его сотрудниками. И мы не только познакомимся с работой научно-исследовательского института, но и сами будем делать открытия!
Научно-исследовательский институт имеет подразделения:
1. Лаборатория экспериментов.
2. Лаборатория научных доказательств.
3. Лаборатория испытаний.
2. Актуализация знаний учащихся. Повторение изученного материала.
«Знание только тогда знание, когда оно приобретено
усилиями своей мысли, а не памятью». Л. Н Толстой.
Это эпиграф нашего урока.
-Ребята, как вы понимаете эту мысль?
- Как вы думаете, почему именно эти слова я подобрала к нашему уроку?
-Ребята, а на что мы должны опираться при получении новых знаний?
-Так что нам нужно сейчас сделать, чтобы подготовиться к изучению нового?
Постараемся усилиями своей мысли приобрести новые знания на уроке.
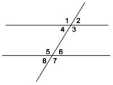 На предыдущих уроках мы с вами изучали признаки параллельности прямых и свойства углов при параллельных прямых. И сегодня на уроке, полученные по этой теме знания, помогут сделать открытие.
На предыдущих уроках мы с вами изучали признаки параллельности прямых и свойства углов при параллельных прямых. И сегодня на уроке, полученные по этой теме знания, помогут сделать открытие.
- Дайте определение параллельных прямых.
(Две прямые на плоскости называется параллельными, если они не пересекаются)
- Назовите по рис. пары углов, которые образуются при пересечении двух параллельных прямых секущей.
- Сформулируйте признаки параллельности прямых.
(Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны; Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны; Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны)
- Сформулируйте свойства углов при параллельных прямых.
(Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны; Если две параллельные прямые пересечены секущей, то соответственные углы равны; Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 1800)
ПОВТОРЕНИЕ ПО ТЕМЕ «ТРЕУГОЛЬНИК»
Давайте повторим, что нам известно о треугольнике?
Учащиеся работают по группам. Им предоставлена возможность общаться друг с другом, каждому самостоятельно строить процесс познания. Что получилось? Каждая группа высказывает свои предложения. Проводится обсуждение результатов:
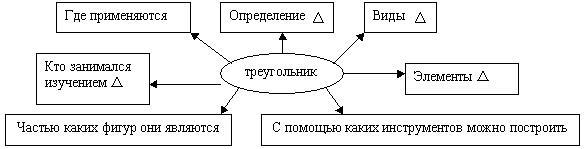
1) Сформулируйте определение треугольника.
(ТРЕУГОЛЬНИК – это фигура, образованная тремя точками, не лежащими на одной прямой, и отрезками, попарно соединяющими эти точки)
2) Назовите элементы треугольника. (Вершины, стороны, углы)
3) Какие треугольники различают? (По сторонам: разносторонние, равносторонние, равнобедренные; карточки – треугольники)
4) Треугольники различают и по углам. Давайте с вами составим рассказ по теме: “УГОЛ”. Для этого используем план:
1. Угол – это фигура, … (Угол – это фигура, образованная двумя лучами, выходящими из одной точки. Лучи называют сторонами угла, а точку – вершиной)
2. Если …, то угол называют … (Если величина угла 900, то угол называют прямым. Если – 1800, то угол называют развернутым. Если больше 00, но меньше 900, то называют острым. Если больше 900, но меньше 1800, то угол называют тупым)
3. Внутренний угол треугольника – это ….
(Внутренний угол треугольника – угол, образованный его сторонами, вершина треугольника является вершиной его угла)
5) Внешний угол треугольника – это… (Внешним углом треугольника называется угол смежный с каким-нибудь углом этого треугольника)
6) Дайте определение развернутого угла, градусная мера развернутого угла.
Значит, в треугольнике углы могут быть различными: тупыми, острыми и прямыми.
Устные задачи на готовых чертежах
3. Изучение нового материала.
Учитель. Наш урок хочется продолжить словами великого русского поэта А.С. Пушкин «Вдохновение нужно в геометрии, как в поэзии»
(Учитель держит в руках треугольник) 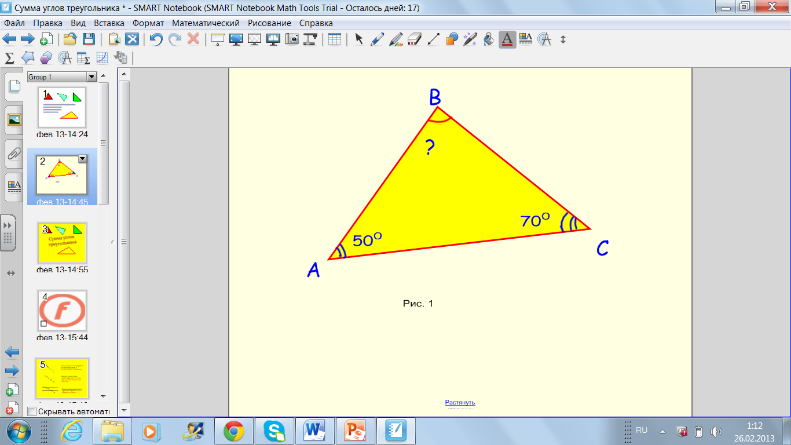
И сегодня мы с вами поговорим о треугольнике, который вдохновлял многих ученых на новые открытия и исследования Треугольник в геометрии играет особую роль. Без преувеличения можно сказать, что вся или почти вся геометрия строится на треугольнике. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о геометрии треугольника как о самостоятельном разделе геометрии.
Создание проблемной ситуации:
- Посмотрите на треугольник (рис. 1). Чему равен В? (постановка проблемы)
В? (постановка проблемы)
(Не выполняя измерений, назовите величину неизвестного угла.)
- Начертите угол: (3 ученика работают у доски, остальные - на месте)
1 – ряд – тупой; 2 – ряд – прямой; 3 – ряд острый.
- Дополните рисунок до треугольника. Что для этого нужно сделать?
(Взять по точке на сторонах угла и соединить их отрезками)
- Полученные треугольники можно назвать: тупоугольными, прямоугольными и остроугольными. (Карточки – треугольники)
Обратите внимание, что у остроугольного треугольника все углы острые.
- Бывают ли треугольники с прямым и тупым углом?
- С двумя тупыми углами?
- С двумя прямыми углами?
- Как это обосновать? Сделать рисунок. К доске выходит ученик и выполняет следующие рисунки:
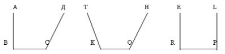
Далее идет коллективное обсуждение:
- Лучи ВА и СД, КТ и ОН, КЕ и PL не пересекаются, значит, треугольник не получится.
- Сумма односторонних углов в I случае больше, чем 1800, во II случае также больше, чем 1800, а в III случае — равна 180°.
- В III случае прямые параллельны, а в первых двух случаях прямые расходятся.
Вывод: что треугольник не может иметь два тупых или два прямых угла. А также в треугольнике не может быть одновременно один тупой и один прямой углы.
- Мы выполнили некоторую практическую работу, сделали обоснование того факта, что треугольник не всегда существует. Его существование зависит от величин углов. Как можно узнать, чему равна сумма углов треугольника?
Практически — измерение, теоретически — рассуждением.
ФИЗКУЛЬТМИНУТКА ДЛЯ ГЛАЗ.
1.Голова неподвижна. Движутся только глаза. В вытянутой руке карандаш. Движение карандаша: влево- вправо- вверх-вниз (3раза)
2.Круговые движения глазами в одном, а затем в другом направлении (6 - 7 раза)
3.Нарисуйте глазами треугольники: маленький, средний, большой
Практическая работа № 1.
На доске и листиках размещены треугольники, которые предложены ребятам для работы.
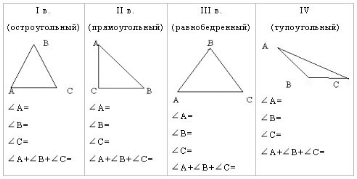
Практическая работа № 2.
Все ребята на местах измеряют произвольный треугольник и с помощью транспортира измеряют углы треугольников, записывают свои измерения и находят сумму углов треугольника.
| Этапы практической работы | Результаты практической работы |
| Постройте произвольный треугольник. |
|
| Измерьте все углы данного треугольника. |
|
| Вычислите сумму углов построенного треугольника. |
|
| Подумайте, зависит ли сумма углов треугольника от его вида? |
|
| Выскажите гипотезу о том, чему равна сумма углов треугольника. |
|
- Что заметили?
- Величина градусной меры суммы углов треугольников близка к 180 градусам.
Выдвигаем гипотезу «Сумма углов треугольника равна 180 градусам»
- Итак, ребята, у вас появилась гипотеза, сумма углов треугольника равна180°. Однако, у многих из вас получились результаты, близкие к 180°, но не 180°. Почему?
Измеряя, мы получаем приближенные значения.
Определение цели урока и построение плана действий
Так вот сегодня на уроке мы попробуем с вами сформулировать и доказать замечательное свойство треугольника «Сумма углов треугольника равна 180°», которое нам поможет ответить на вопрос, поставленный вначале урока. Чему равен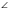 В?
В?

ИСТОРИЧЕСКАЯ СПРАВКА: (СООБЩЕНИЕ УЧЕНИКА)
Сумма углов треугольника была практическим путем установлена, еще в Древнем Египте. Теорема о сумме углов треугольника – одна из важнейших теорем в геометрии. Её доказательство приписывают древнегреческому математику Пифагору, который жил в V веке до нашей эры.
Однако у нас с вами есть гипотеза: сумма углов треугольника равна 180°, которую можно проверить еще одной практической работой: где еще сегодня называли это число? Величина развернутого угла.
Практическая работа № 3.
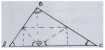 У вас на столах лежат треугольники из бумаги (остроугольные, тупоугольные, прямоугольные).
У вас на столах лежат треугольники из бумаги (остроугольные, тупоугольные, прямоугольные).
I вариант. На столах лежат треугольники. Путем перегибания соберем углы треугольника в одну точку.
Что у нас получилось? Что сумма углов треугольника равна 1800.
II вариант. Используя модели треугольников, определить, какой угол получится, если его составить из углов треугольника. Чему равна его градусная мера? (Углы треугольников можно отрывать.)
Далее ученики говорят результаты своего эксперимента, результаты появляются на слайдах.

Вывод: Проверяя результаты измерений углов треугольников различного вида, практическая работа показала, что сумма углов любого треугольника равна 180°.
Практическая работа № 4.
(работа с моделями на партах и на доске).
- Давайте посмотрим, как еще можно увидеть, что сумма углов треугольника рана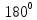 .
.
(На каждой парте лежат по 3 равных треугольника).
- Перед вами на столе три равных треугольника. Как можно в этом убедиться? Наложите один треугольник на другой, и вы проверите это.
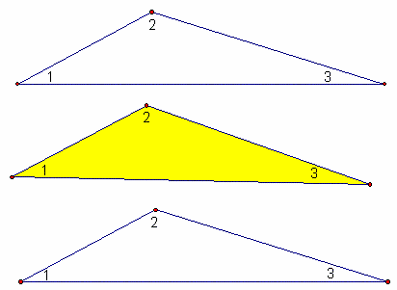
Положите цветной треугольник на стол, а два других треугольника положите рядом с первым таким образом, чтобы у одной вершины оказалось три разных угла, а стороны их совпадали.
Учитель помогает учащимся, а затем выполняет указанные действия на доске (треугольники крепятся при помощи магнитов).

Посмотрите внимательно, что у вас получилось?
Как называется угол, который составляют вместе
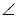 1,
1, 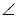 2 и
2 и 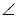 3?
3? Какова градусная мера этого угла?
Значит, чему равна сумма углов 1, 2 и 3?
Чему равна сумма равных им углов цветного треугольника?
Какой теперь мы можем сделать вывод о сумме углов треугольника?
Итак, мы выяснили практическим путем, что сумма углов треугольника равна 1800.
ЛАБОРАТОРИЯ НАУЧНЫХ ДОКАЗАТЕЛЬСТВ.
Теперь мы попытаемся доказать это утверждение.
Теорема о сумме углов треугольника - это одна из самых важных теорем геометрии.
Для этого перейдем в лабораторию доказательств и здесь мы с вами докажем научно, что это действительно так!
РАБОТА НАД СТРУКТУРОЙ ТЕОРЕМЫ.
Чтобы сформулировать теорему, ответьте на следующие вопросы:
Какие треугольники использовались в процессе проведения измерений?
Что входит в условие теоремы (что дано)?
Что мы обнаружили при измерении?
В чем состоит заключение теоремы (что надо доказать)?
Попробуйте сформулировать теорему о сумме углов треугольника.

Записываем формулировку нашего открытия – теорему.
Теорема: Сумма углов треугольника равна 1800.
Построение чертежа и краткая запись теоремы
(устное обсуждение)
Дано:  АВС
АВС
 1,
1,  2,
2,  3 – внутренние
3 – внутренние
Доказать:  1+
1+  2+
2+ 3=1800
3=1800
Доказательство: Попробуем доказать теорему, “собрав” все углы треугольника в одну вершину (на доске выполняется чертеж). “Собрать углы” - значит, “взять углы”, равные данным.
Когда  4=
4= 1 (
1 ( 5=
5= 3)? (При параллельности прямой а и стороны АС)
3)? (При параллельности прямой а и стороны АС)
Известно:
 5 +
5 + 2 +
2 +  4 =180°. (развернутый угол)
4 =180°. (развернутый угол)
 1 +
1 + 2+
2+  3 = 180°.
3 = 180°.
ПЛАН ДОКАЗАТЕЛЬСТВА:
- провести прямую через одну из вершин параллельно противолежащей стороне;
- составить пары равных накрест лежащих углов;
- представить развернутый угол в виде суммы углов;
- заменить слагаемые равными им углами треугольника.
ПОВТОРИТЬ ТЕОРЕМУ, ДЕЛАЯ КРАТНУЮ ЗАПИСЬ:
ДАНО:  АВС,
АВС,  1,
1,  2,
2,  3 - внутренние.
3 - внутренние.
ДОКАЗАТЬ:  1 +
1 + 2 +
2 +  3 = 180°.
3 = 180°.
ДОКАЗАТЕЛЬСТВО:
1) Проведем через т. В прямую а || АС. (аксиома параллельных прямых)
При вершине В получились 3 угла, которые в сумме составляют развернутый угол,
т.е.  4,
4,  2,
2,  5
5
2)  5 =
5 =  3 (внутренние накрест лежащие при а
3 (внутренние накрест лежащие при а АС и секущей ВС )
 4 =
4 = 1 (внутренние накрест лежащие при а
1 (внутренние накрест лежащие при а АС и секущей АВ)
3)  5 +
5 + 2 +
2 + 4 = 180°. (развернутый угол)
4 = 180°. (развернутый угол)
4) Заменим в равенстве (3)  5 на
5 на  3 ,
3 ,  4 на
4 на  1 и получим
1 и получим  1 +
1 +  2 +
2 + 3 = 180°.
3 = 180°.
Или А+
В+
С=1800. Что и требовалось доказать.
Следствия теоремы:
В любом треугольнике все углы острые; либо два угла острых, а третий тупой или прямой.
Теорема позволяет классифицировать треугольники не только по сторонам, но и по углам.
| Вид треугольника | Равнобедренный | Равносторонний | Разносторонний |
|
прямоугольный | |
|
|
|
тупоугольный |
|
|
|
|
остроугольный |
|
|
|
4. Закрепление нового материала:
ЛАБОРАТОРИЯ ИСПЫТАНИЙ (ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ)
1. Чему равен третий угол в треугольнике, если один из углов 40°, второй 60°? (80°)
2. Чему равен угол равностороннего треугольника? (60°)
3. Чему равна сумма острых углов прямоугольного треугольника? (90°)
4. Чему равен острый угол прямоугольного равнобедренного треугольника? (45°)
5. Задачи по готовым чертежам. (Cлайды19-24).
6. Решение задач из учебника №225, № 228 (рассмотреть 2 случая) (Слайды 28-29.)
7. В каком треугольнике сумма углов больше: в остроугольном, тупоугольном или прямоугольном?
8. Можно ли измерить углы любого треугольника?
Это вопрос-шутка, т.к. существует Бермудский треугольник, находящийся в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида, у которого невозможно измерить углы.
Применение:
Метод триангуляции в геодезии;
В астрономии – астрономы определяют положение звезд при помощи сферических треугольников.
Сегодня мы сделали научное открытие: сумма углов треугольника равна 180°.
Мы узнали, как в жизни происходит открытие, т.е. как ученые делают открытия, их доказывают и находят применения своим открытиям.
5. Итог урока, выставление оценок:
Какую мы сегодня изучали теорему?
Было ли на уроке легко, интересно?
Ребята, как вы считаете достигли мы целей урока?
Получили новые знания, «усилием мысли»?
Развивайте свою мыслительную деятельность, логическое мышление, ведь, это богатство, которое нельзя потерять, а можно только приумножить, а для этого нужна постоянная тренировка.
С одной стороны, треугольник – это геометрическая фигура, с другой стороны треугольник это - тайный оккультный знак, встречающийся во многих цивилизациях. Три угла, три грани - магическое число 3. Не удивительно, что треугольник можно найти на тайных письменах, символах, пентаграммах. И совсем не удивительно, что самые загадочные места и строения могут быть связаны тоже с треугольниками. Например, египетские пирамиды (в Египте треугольник символизировал триаду духовной воли, любви-интуиции и высшего разума человека, то есть его личность и душу.) Или звезда Давида (еврейский символ, образованный наложением двух треугольников). А еще Бермудский треугольник.
Оцените своё настроение на уроке:
хорошее равнодушное плохое
6.Домашнее задание: § 30, 223 (а, б), 228 (в), № 229 (по желанию),
Индивидуально карточки (по желанию)
ЛИТЕРАТУРА
Геометрия. 7-9 класс. учебник / Л.С.Атанасян, В.Ф.Бутузов и др. Москва: Просвещение, 2017
Универсальные поурочные разработки по геометрии. 7 класс/ Н.Ф.Гаврилова Москва. «ВАКО». 2013
7 класс Геометрия. Поурочные планы. / Т.Л.Афанасьева, Л.А.Тапилина. Волгоград: Учитель, 2016.
ПРИЛОЖЕНИЕ 1
Предлагаю вам дома придумать другие способы доказательства теоремы, используя чертежи, которые у вас на обратной стороне листа с «Фразой дня»
Карточка для индивидуального домашнего задания.
|
Докажите теорему о сумме углов треугольника, используя чертеж учеников Пифагора.
|
ПРИЛОЖЕНИЕ 2
Доказательство теоремы «Суммы углов треугольника» с применением теоремы о сумме внутренних односторонних углов при параллельных прямых и секущей
План доказательства теоремы.
Через одну из вершин треугольника провести прямую, параллельную противолежащей стороне.
Доказать равенство накрест лежащих углов.
Записать сумму односторонних углов и выразить их через углы треугольника.
Доказательство и его запись.
Проведем BD || АС (аксиома параллельных прямых).
Ð3 = Ð4 (так как это накрест лежащие углы при BD || АС и секущей ВС).
ÐА + ÐАВD = 180° (так как это односторонние углы при BD || АС и секущей АВ).
ÐА + ÐАВD = Ð1 + (Ð2 + Ð4) = Ð1 + Ð2 + Ð3 = 180°, что и требовалось доказать.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Сумма углов треугольника. Конспект урока. (357.62 KB)
Сумма углов треугольника. Конспект урока. (357.62 KB)
 0
0 1327
1327 97
97 Нравится
0
Нравится
0


