Сумма n первых членов арифметической прогрессии

ТЕМА: «СУММА n ПЕРВЫХ ЧЛЕНОВ АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ».

Разработка урока в 9 классе по алгебре

Учитель МБОУ СШ № 56 города Красноярска

Рожкова Виктория Викторовна

ЦЕЛИ УРОКА:

• Знать формулу n первых членов арифметической прогрессии.
• Уметь использовать формулу суммы при решении задач.
• Выработать навык решения задач с использованием формул суммы n первых членов арифметической прогрессии.

ЭПИГРАФ К УРОКУ

Стевин писал:

«мы приходим к выводу, что

не существует никаких абсурдных,

иррациональных, неправильных, необъяснимых

или глухих чисел, но что среди чисел

существует такое совершенство

и согласие, что нам надо размышлять

дни и ночи над их удивительной закономерностью».

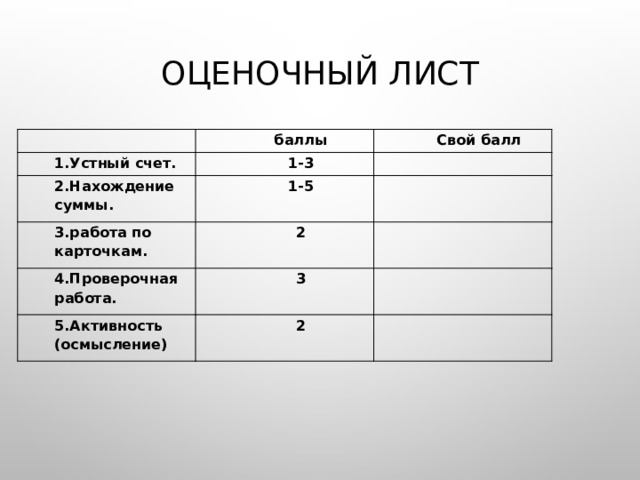
ОЦЕНОЧНЫЙ ЛИСТ

баллы

1.Устный счет.

Свой балл

1-3

2.Нахождение суммы.

1-5

3.работа по карточкам.

4.Проверочная работа.

2

3

5.Активность (осмысление)

2

Установите закономерность и продолжите последовательность:

1)Назовите следующий член последовательности;

2)Укажите закономерность;

3) Как называется данная последовательность?

4) Найдите 10-й член этой последовательности.

5)Как найти n-й член любой последовательности?

6) Найдите сумму первых двух (трех) чисел.

а) 6, 8, 10, …

б) 25, 21, 17, …

1.Какая числовая последовательность называется арифметической прогрессией?

2.Назовите формулу n – го члена арифметической прогрессией.

3. Найдите сумму всех натуральных чисел от 1 до 100.

1+2+3+4+5+…+100

Немецкий математик К.Ф.Гаусса

«Сосчитать сумму всех натуральных чисел от 1 до 40 включительно: 1+2+3+…+40»

Вот схема его рассуждений: «сумма чисел в каждой пар равна 41

+1, 2, 3, 4, …, 40

40, 39, 38, 37, …, 1

----------------------------

41, 41, 41, 41, …, 41

Таких пар 20, поэтому искомая сумма равна 41*20=820».

Что же, попробуем применить эти рассуждения для решения нашей задачи:

+S = 1+2+3+4+5+…+100

S = 100+99+98+97+96+…1

--------------------------------------

2S = 101+101+101+101+101+…+101

2S = 101*100

S = (101*100):2=5050

• Запишем S n двумя способами:
• S n = a 1 + a 2 + … + a n-1 + a n
• S n = a n + a n-1 + … + a 2 + a 1
• По определению арифметической прогрессии эти равенства можно записать так:
• +S n = a 1 + (a 1 + d) + (a 1 + 2d) + … + (a 1 + (n-1)d)
• S n = a n + (a n – d) + (a n – 2d) + … + (a n – (n-1)d)
• ------------------------------------------------------------
• 2S n = (a 1 + a n ) + (a 1 + a n ) + … + (a 1 + a n )
• N слагаемых

Следовательно, 2S n = (a 1 + a n ) * n

S n =

Закрепим данную формулу: найдем сумму шестидесяти первых четных натуральных чисел.

( an) – арифметическая прогрессия: 2, 4, 6, 8, …

a1 = 2 an = 2n = 2*60 = 120 = a60

n = 60

S60 = (a_1+ a_60 )/2*60= (2+120)/2*60=122*30=3660

Сейчас поработаем в группах, на карточках даны задания. Ваша задача найти сумму n первых членов арифметической прогрессии и занести свой ответ в карту ответов.

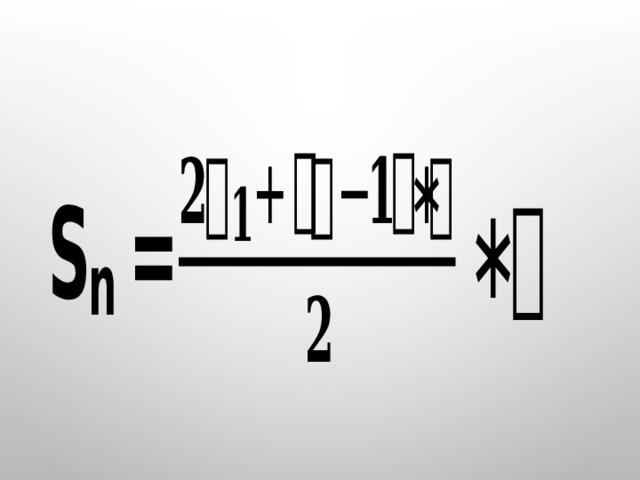
Проверочная работа.

1 вариант

2 вариант

Найдите десятый член арифметической прогрессии и сумму ее первых десяти членов, если а1 = -8, d = 2.

Найдите девятый член арифметической прогрессии и сумму ее первых девяти членов, если а1 = 2, d = -4.

Домашнее задание .

§ 29 стр. 143 № 391, 392, 393(2)

Итог урока.

Вопрос: Рассуждения какого ученого нам сегодня помогли?

Сколько формул существует для нахождения суммы?

Подведем итог нашей работы и внесем в последнюю графу свои баллы. Подсчитайте количество баллов и оцените работу:

13 – 15 –«5»

10 – 12 – «4»

7 – 9 – «3»

Сдайте оценочные таблицы.