Обучение, согласно ФГОС, больше не заключается в том, что ученик получает от учителя некую информацию и осваивает её. Сегодня ученику необходимо самостоятельно строить своё знание, добывать информацию, критично оценивать свои действия.
В настоящее время все более актуальным в образовательном процессе становится использование методов, которые формируют умения самостоятельно добывать знания, собирать необходимую информацию, выдвигать гипотезы, делать выводы и умозаключения, сравнивать. Это требует достаточного уровня сформированности некоторых мыслительных качеств, в частности дивергентности.
В различных источниках дивергентное мышление трактуется следующим образом.
В википедии [1] даётся следующее определение: "Дивергентное мышление (от лат. divergere – расходиться) — метод творческого мышления, применяемый обычно для решения проблем и задач. Заключается в поиске множества решений одной и той же проблемы. Исследованиями дивергентного мышления занимались Д. Гилфорд, К. Тейлор, Г. Груббер, И. Хайн, А. Б. Шнедер, Д. Роджерс."
По Дж. Гилфорду [2,3], дивергентное мышление есть мышление, направленное на поиск разнообразных логических возможностей, мышление, идущее в различных направлениях. Основанием дивергентного мышления является порождение множества решений на основе однозначных данных. Дивергентные способности (divergence), дивергентные операции, дивергентное мышление ‑ термины, раскрываемые Дж. Гилфордом для описания процесса выдвижения различных и в равной мере правильных идей относительно одного и того же объекта или при решении одной и той же задачи.
А. Н. Иванов в своем исследовании пришел к выводу, что понятие «дивергентное мышление» в самом общем виде отражает способность к видению альтернатив, а дивергентность есть особое качество мышления, позволяющее видеть несколько путей решения проблемы. Собственно «дивергентность мышления – это умение найти несколько способов решения задачи, способность увидеть вариативность ответов и решений» [3, с. 97].
Считается, что дивергентное мышление является одним из компонентов творчества. Учитывая специфику обучения математике в школе, дивергентные умения можно охарактеризовать быстротой поиска разнообразных путей решения задачи и высказывания идей, допускающих различные неожиданные ассоциативные переходы, гибкостью, оригинальностью и точностью, лаконичностью итоговой мысли. К дивергентным умениям в контексте работы с математическими задачами можно отнести:
- умение анализировать исходные данные задачи и верно их интерпретировать;
- умение изменять направление поиска в процессе нахождения ответов на различные вопросы;
- умение генерировать различные пути решения проблемы, что может приводить к неожиданным результатам;
- умение находить альтернативные по отношению к приведенным пути решения проблемы;
- умение самоопределяться в ситуации неопределенности;
- умение системно и целостно подходить к решению поставленной проблемы и др.
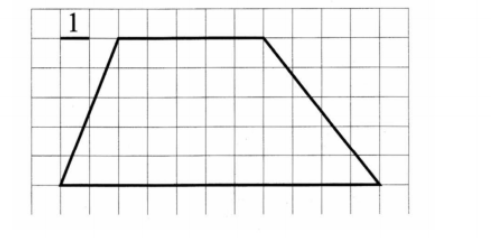
Например, задача ОГЭ [4, стр.13] : "Найдите площадь трапеции, изображённой на рисунке", имеет сразу несколько способов решения.
Первый - графический - используется учениками начальной школы. Вся фигура разбивается на квадратики, подсчитывается количество целых квадратиков (25), а "неполные" квадратики выделяют в два треугольника, каждый из которых дополняют до прямоугольника (в состав которого входят два одинаковых искомых треугольника) и, вспоминая состав числа (10 = 5+5; 20 = 10+10), находят площадь "полных" квадратиков (15). В итоге получается 40.

Второй - геометрический - доступен ученикам средней школы, изучившим площади геометрических фигур. Дополняем трапецию до прямоугольника со сторонами 11 ед. и 5 ед. Площадь такого прямоугольника находится легко и составляет 55 ед.кв. Остаётся отнять от этой площади площади двух треугольников, равные соответственно 1/2*2*5 = 5 и 1/2*4*5 = 10. Таким образом получаем снова: 55 - 5 - 10 =40.
Третий - аналитический: необходимо подставить в формулу площади трапеции соответствующие значения оснований (5 и 11) и высоты (5). Таким образом, 1/2*(5+11)*5 = 40.
Приведённое задание способствует умению самоопределяться в ситуации неопределённости, так как в самом условии задания не оговаривается, каким именно способом необходимо решить поставленную задачу. Это даёт простор для анализа условия задачи и поиска пути её решения, после чего требуется самоопределиться с путём достижения ответа.
Но если наша цель - развитие дивергентного мышления у учащихся, то эту задачу следует переформулировать следующим образом: "Найдите несколькими способами площадь трапеции, изображённой на рисунке". В этом случае задача становится направленной на формирование именно поиска различных одинаково правильных путей решения, т.е. на формирование дивергентных умений. В этом случае ни одно из решений не отвергается, так как основная цель - предложить как можно больше путей решения данной задачи, а не сравнивать их по степени трудности.
Эту же цель - развитие дивергентного мышления, можно реализовать при решении квадратных уравнений. Задание будет выглядеть так: решите квадратное уравнение несколькими аналитическими способами.
х2 - 6*х + 8 = 0
Представляется возможным решение четырьмя различными способами.
Первый - метод выделения полного квадрата.
х2 - 6*х + 8 = 0
х2 - 2*х*3 + 32 - 12 = 0
(х-3)2 - 12 = 0
(х-3+1) (х-3-1) = 0
(х-4) ( х-2) = 0
х1 = 4; х2 = 2
Второй - метод разложения на множители.
х2 - 6*х + 8 = 0
х2 - 2х - 4х + 8 =0
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Статья на тему "Формирование дивергентных умений на уроках математики" (0.11 MB)
Статья на тему "Формирование дивергентных умений на уроках математики" (0.11 MB)
 0
0 1245
1245 22
22 Нравится
0
Нравится
0




