План – конспект урока по информатике
в рамках подготовки учащихся к ЕГЭ
по теме: «Системы счисления»
Цель урока: создать содержательные и организационные условия для применения школьниками комплекса знаний по теме «Системы счисления» для решения задач, включаемых в материалы ЕГЭ.
Задачи урока:
Образовательные:
систематизировать знания учащихся по теме «Системы счисления»;
научить учащихся использовать рациональные методы перевода чисел между системами счисления.
Развивающие:
развивать личностно-смысловые отношения учащихся к изучаемому предмету;
развитие мышления, памяти;
формирование навыков логического мышления (вывод, анализ, обобщение, выделение главного).
Воспитательные:
формировать навык самостоятельной работы;
формировать интерес к предмету;
формировать навык решения тестовых заданий;
актуализация и приспособление возможностей личности для успешных действий в ситуации сдачи экзамена.
Оборудование урока:
дидактический материал (приложение 2-3);
Ход урока:
Организационный момент.
Постановка целей урока. Мотивация учащихся. – 1 мин
Повторение некоторых рациональных способов перевода чисел из одной с.с. в другую – 7 мин
Объяснение нового материала. – 20 мин
Закрепление изученного материала. – 15 мин
Подведение итогов. – 2 мин
План-конспект урока
| Этапы урока | |||
| 1. Организационный момент. | |||
| 2. Постановка целей урока. Сегодня у нас обобщающий урок по теме: «Системы счисления». Данная тема изучается вами в 10 классе, а задания по данной теме встречаются в материалах ЕГЭ. Сегодня мы систематизируем знания по данной теме, научимся применять полученные знания для решения комплекса задач, включаемых в материалы ЕГЭ. | |||
| 3. Повторение некоторых рациональных способов перевода чисел из одной с.с. в другую | |||
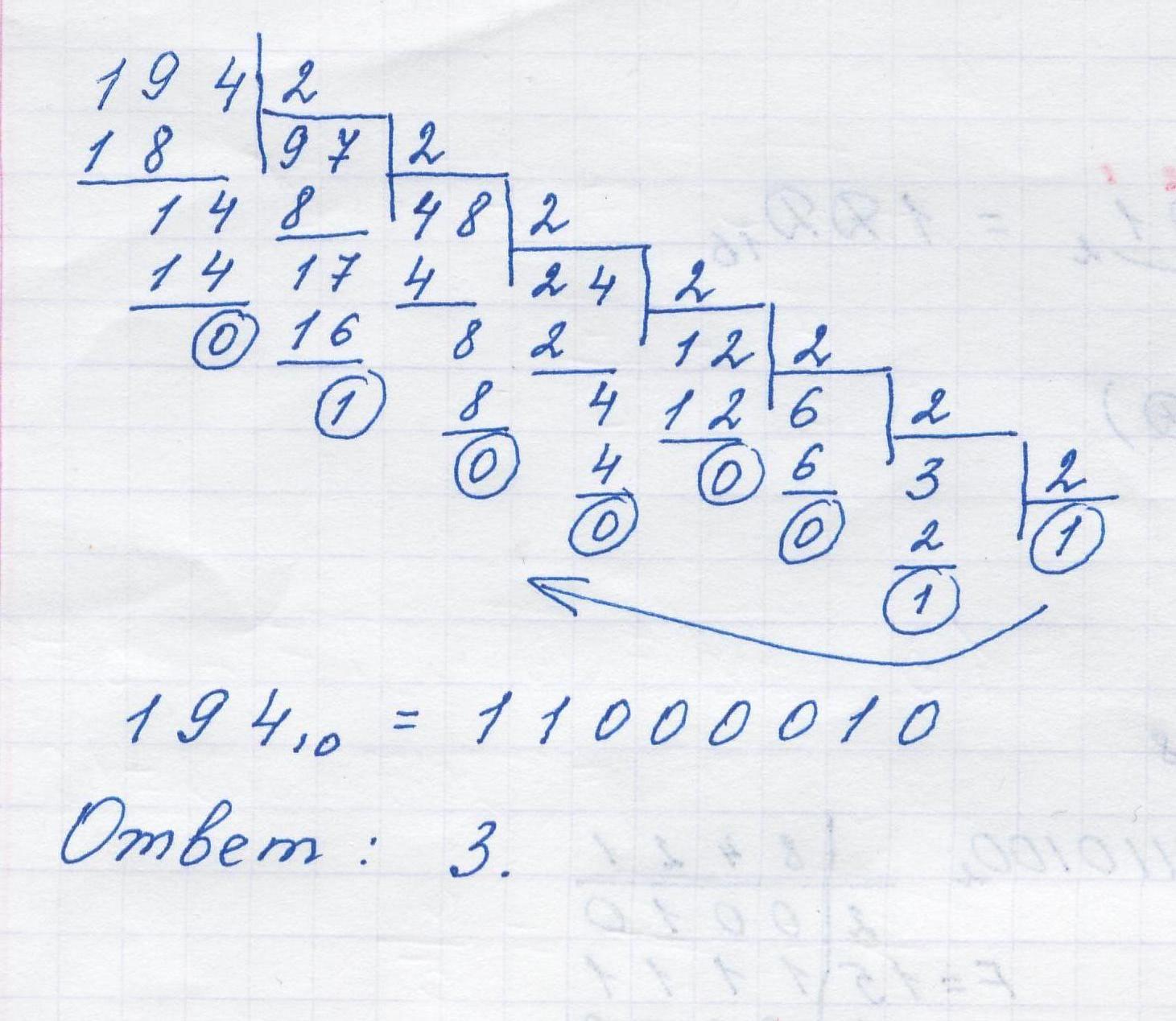
| Сколько единиц используется в двоичной записи числа 194? (некоторые учащиеся используют стандартный прием: алгоритм «Деление уголком», поэтому стараюсь вызвать к доске именно такого ребенка) | один из учеников решает у доски, остальные в тетради. Возможны варианты решения: 1вариант решения Для выполнения этого задания мы должны выполнить перевод 19410 → Х2
| ||
| Согласны ли вы с тем, что деление уголком слишком громоздкая запись? | 2 вариант решения
Целые степени числа2: 128 64 32 16 8 4 2 1 1 1 0 0 0 0 1 0
194-128=66 66-64=2
19410 = 110000102
Ответ: 3 | ||
|
А теперь выполните перевод 101000012Х10, используя целые степени числа 2. Ответ: 16110 |
один из учеников решает у доски, остальные в тетради.
Целые степени числа2: 128 64 32 16 8 4 2 1 1 0 1 0 0 0 0 1
128+32+1=16110
Ответ: 161
| ||
| веселая викторина – устная работа Сколько глаз у пиявки? (подсказка 10102) Сколько вершков в аршине (подсказка: 100002) Сколько лет спала Спящая красавица из сказки Шарля Перро? (подсказка: 11001002) Сапоги какого размера носил дядя Степа?(подсказка: 1011012) Сколько лет было Красной шапочке? (подсказка 10002)
Ответы: 10, 16, 100, 45, 8 | Учащиеся записывают в тетради ответы на вопросы
| ||
| Выполните перевод: 7358Х2Х16 Ответ: 735811101110121DD16
|
один из учеников решает у доски, остальные в тетради.
7358Х2
7 1 1 1 3 0 1 1 5 1 0 1 Чтобы перевести число из 2с.с. в 16с.с. надо разбить это число влево и вправо от запятой на двоичные тетрады и каждую такую тетраду заменить эквивалентной ей 16-ой цифрой: 1 8 4 2 1 8 4 2 1 1 D D (8+4+1=13=D)
| ||
| Выполнить перевод 2F416Х2Х8 Ответ: 2F4161011110100213648 |
один из учеников решает у доски, остальные в тетради.
2F416X2
2 0 0 1 0 F=15 1 1 1 1 4 0 1 0 0
Чтобы перевести число из 2с.с. в 8с.с. надо разбить это число влево и вправо от запятой на двоичные триады и каждую такую триаду заменить эквивалентной ей 8-ой цифрой:
| ||
| 4. Объяснение нового материала Теперь, когда учащиеся вспомнили основные алгоритмы перевода чисел из одной с.с. в другую, приступаем к разбору заданий ЕГЭ | |||
| А-1. Дано число а=9216 и число в=2248. Какое из чисел с, записанных в двоичной системе счисления удовлетворяет условию: acb? 10010011 10001110 10001010 10001100
|
| ||
|
| |||
| А-2. Чему равна сумма чисел 438 и 5616? 1218 1718 6916 10000012 |
| ||
| А-3. Вычислите значение суммы в 10с.с.: 102+108+1016=? 3010 2610 3610 2010 | Решение: 1. 102Х10 21 102=210 2. 108Х10 10 108=1*81+0*80=810 3. 1016Х10 10 1016=1*161+0*160=1610 4. 210+810+1610=2610
Ответ: А-3-2 | ||
| В-1. Укажите через запятую в порядке возрастания все основания систем счисления в которых запись числа 16 оканчивается на 1. | Дано: 1610=?1х Найти: Х 1 вариант решения: Для того, чтобы целое число 16 перевести из 10с.с. его надо разделить наХ - основание новой системы счисления. Первый остаток от деления даст нам последнюю цифру нового числа в новой с.с. (необходимо по условию получить цифру 1). Нам надо проверить какое Х из промежутка от 2 до 16 удовлетворяет нашему условию. 16 mod 2=0 16 mod 3 = 1 16 mod 4 = 0 16 mod 5 = 1 16 mod 6 = 4 16 mod 7 = 2 16 mod 8 = 0 16 mod 9 = 7 16 mod 10 = 6 16 mod 11 = 5 16 mod 12 = 4 16 mod 13 = 3 16 mod 14 = 2 16 mod 15 = 1 16 mod 16 = 0 Ответ:3,5,15 2 вариант решения Для того, чтобы целое число 16 перевести из 10с.с. его надо разделить наХ - основание новой системы счисления. Первый остаток от деления даст нам последнюю цифру нового числа в новой с.с. (необходимо по условию получить цифру 1). Решаем уравнение: 16 mod Х = 1 x*d+1=16 x*d=15 x=15/d (т.к. мы ищем основание с.с., то Х может быть только целым числом из диапазона от 1 до 16, следовательно d – это делители числа 15, т.е. d=1,3,5,15) тогда Х=3,5,15,1, х=1 не удовлетворяет решению задачи. Ответ х=3,5,15
| ||
| В-2. Укажите через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в 2с.с. оканчивается на 101. Числа в ответе указать в 10с.с. | Дано: Х=?1012 Найти: Х (где 2X 1 вариант решения Переведем все числа от 2 до 25 в 2с.с. и посмотрим, какие из них оканчиваются на 101. 210=102 310=112 410=1002 510=1012 610=1102 710=1112 810=10002 910=10012 1010=10102 1110=10112 1210=11002 1310=11012 1410=11102 1510=11112 1610=100002 1710=100012 1810=100102 1910=100112 2010=101002 2110=101012 2210=101102 2310=101112 2410=110002 2510=110012 Ответ: 5,13,21 2 вариант решения Для того, чтобы перевести число ?1012 в10с.с. его надо разложить в степенной ряд и подсчитать результат, возможны случаи: 1012=22+20=510 11012=23+22+20=1310 101012=24+22+20=2110 111012=24+23+22+20=2910 (не удовлетворяет условию 2X Ответ: 5,13,21
| ||
| 5. Закрепление изученного материала Самостоятельная работа учащихся. Учащиеся получают тексты заданий для индивидуального решения (приложение 2) | |||
| 6. Подведение итогов Домашнее задание – приложение 3. | |||
Приложение 2.
Вариант 1
Самостоятельная работа состоит из двух частей А и В.
Часть А содержит три задания с выбором ответа. К каждому заданию даются четыре ответа, из которых только один правильный. При выполнении заданий данной части в бланке ответов под номером выполняемого вами задания поставьте знак «х» в клеточку, номер которой соответствует номеру выбранного вами ответа.
Часть В состоит из одного задания (к этому заданию вы должны самостоятельно сформулировать и записать ответ в бланк ответов справа от номера соответствующего задания, начиная с первой клеточки, каждый символ пишите в отдельной клеточке.)
Желаю успехов!!!
| Фамилия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Имя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А1. Как представлено число 8310 в двоичной системе счисления?
10010112
11001012
10100112
| А1 |
|
|
|
|
|
| 1 | 2 | 3 | 4 |
А2. Дано а=D716, b=3318. Какое из чисел с, записанных в двоичной системе отвечает
условию acb?
110110012
110111002
110101112
110110002
| А2 |
|
|
|
|
|
| 1 | 2 | 3 | 4 |
А3. Чему равна разность чисел 10116 и 11001012?
448
2348
3616
6016
| А3 |
|
|
|
|
|
| 1 | 2 | 3 | 4 |
В1. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11.
| В1 |
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 2
Самостоятельная работа состоит из двух частей А и В.
Часть А содержит три задания с выбором ответа. К каждому заданию даются четыре ответа, из которых только один правильный. При выполнении заданий данной части в бланке ответов под номером выполняемого вами задания поставьте знак «х» в клеточку, номер которой соответствует номеру выбранного вами ответа.
Часть В состоит из одного задания (к этому заданию вы должны самостоятельно сформулировать и записать ответ в бланк ответов справа от номера соответствующего задания, начиная с первой клеточки, каждый символ пишите в отдельной клеточке.)
Желаю успехов!!!
| Фамимлия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Имя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А1. Количество нулей в двоичной записи числа 129 равно:
5
6
7
| А1 |
|
|
|
|
|
| 1 | 2 | 3 | 4 |
А2. Дано а=3716, b=718. Какое из чисел с, записанных в двоичной системе отвечает
условию acb?
1). 111000
2). 110100
3). 111100
| А2 |
|
|
|
|
|
| 1 | 2 | 3 | 4 |
А3. Чему равна сумма чисел 278 и 3416?
1100112
638
5116
1138
| А3 |
|
|
|
|
|
| 1 | 2 | 3 | 4 |
В1. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 19 оканчивается на 4.
| В1 |
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 3
Домашнее задание.
А1.Дано а=9716, в=2318. Какое из чисел с, записанных в двоичной системе счисления, отвечает условию acb?
1). 10011001 2). 10011100 3). 10000110 4). 10011000
А2. Чему равна сумма чисел 728 и 1D16.
1). 100011112 2). 11001012 3). 1010112 4). 10101112
В1. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 11 оканчивается на 1.

 Получите свидетельство
Получите свидетельство Вход
Вход


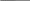
 4 2 1 7358=1110111012
4 2 1 7358=1110111012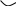
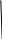
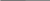 8 4 2 1 2F416=101111101002
8 4 2 1 2F416=101111101002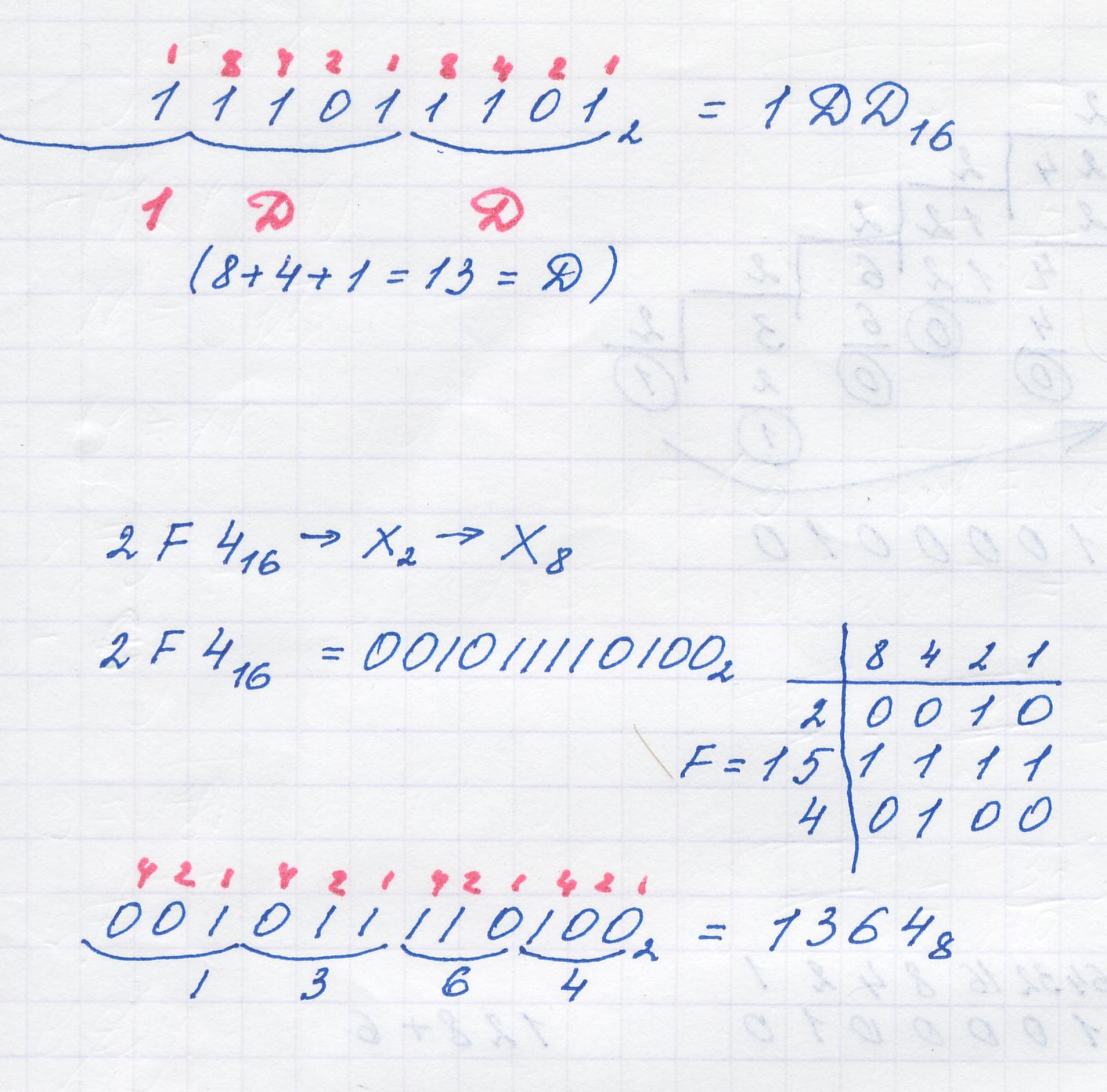










 План – конспект урока по информатике "Системы счисления" 9 класс (1.78 MB)
План – конспект урока по информатике "Системы счисления" 9 класс (1.78 MB)
 0
0 393
393 9
9 Нравится
0
Нравится
0


