Статья "Исследование на уроках математики"

Исследования на уроках математики

Рублёва Т.Я., преподаватель математики высшей квалификационной категории, заслуженный учитель РФ.

ФГКОУ «Тюменское президентское кадетское училище»

Аннотация: в статье рассматриваются элементы исследовательской работы на уроках математики.

(Краткий обзор опыта работы).

Так кто же он, человек из детства? Сосуд, который надо наполнить знаниями? Факел, который надо зажечь? Сравнения, как всегда хромают, и всё куда сложнее. Обучать, как я понимаю этот термин, - это обучать какому-то виду деятельности, как принято говорить, «учат учиться». Это само по себе неплохо. Но замыкает образовательный процесс на себе. Можно попытаться сделать чуть больше. Именно – обучать основам научно-исследовательской деятельности.

Технологии проведения исследовательских работ предполагают три вида работ: элементы исследования на уроке, интенсивная работа над исследовательскими задачами в аудиторное время. Это можно делать, например, в рамках летней школы или специальной проектной неделе в училище, индивидуальная работа в свободное время с консультациями учителя с выходом на научно- практическую конференцию.

Считаю, что содержательная исследовательская работа по математике на уроке возможна и полезна.

Что такое исследовательские задачи.

Выделим два подхода к обучению. При одном – назовем его традиционным – ученик изучает новую теорию, решает задачу, получает оценку и ждёт от учителя новой задачи. Предполагается, что у задачи есть единственный правильный ответ и учитель его знает. При другом подходе – назовём его исследовательским – ученик сам ставит вопросы и ищет на них ответы, выдвигает гипотезы, доказывает и опровергает их. Всякий полученный ответ может стать основанием для новых вопросов. Результат может быть не известен учителю заранее. Можно сказать, что ученик попадает в новый математический мир и учится жить в нём.

Три мнения об исследовательских задачах:

«Они доступны только старшеклассникам».

«Они нужны только сильным школьникам».

«Учёба отдельно, исследования отдельно».

Считаю, что всё это не так. Чтобы начинать решать такие задачи, не надо ждать старших классов, уже материал начальной школы позволяет вводить элементы исследования. Полезно начинать с самого простого, с вещей, доступных несильным ученикам. Далее, хорошее обучение должно дать понятие о методах, характерных для изучаемой науки. При работе с исследовательскими задачами ученикам неизбежно приходится иметь дело с методами науки математики, поэтому исследовательские задачи могут стать органической частью обучения математике. 

Отметим, что всякую содержательную олимпиадную задачу можно рассматривать как «кусочек», вырезанный из какой-то исследовательской темы (часто для её решения достаточно восстановить контекст. Новизна здесь не в задаче, а в подходе к работе школьника: не «решил-не решил», а «какую часть нового математического мира освоил». По сути, задача здесь рассматривается как «зацепка» для введения в тему исследования.

Приведу примеры несложных исследовательских задач из разных разделов математики.

Формула Пика.

Найти площади многоугольников, изображенных на рисунке.

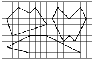
На клетчатой бумаге нарисован многоугольник с вершинами в узлах клеток. Как найти его площадь, подсчитывая лишь количества узлов?

Примерный план. Экспериментально ищем формулу для треугольника 1) без узлов внутри и на сторонах, 2) с узлами на сторонах, 3) с узлами внутри, 4) с узлами внутри и на сторонах. Придумываем общую формулу. Повторяем исследование для 4-угольников и для 5-угольников. Объединяя результаты, придумываем формулу для n-угольника. Доказываем её (сумма «площадей» двух многоугольников равна «площади» их объединения). Затем доказываем её справедливость последовательно для прямоугольника, прямоугольного треугольника, произвольного треугольника, произвольного многоугольника.

Обобщение. Решить аналогичную задачу для многогранников в пространстве.

S= n + m/2 -1 N- узлы внутри решетки, m- узлы на границе.

Крылатые числа.

Если число можно представить в виде c²+4de, то его представление в этом виде можно представить геометрически. Начнём так делать:

5

=

e=dd

17

=

=

=

=

=

Восстановление многоугольника.

На доске нарисован многоугольник. Отметили середины его сторон, а сам многоугольник стёрли. Как восстановить многоугольник по серединам сторон? Сколько решений имеет задача?

Исследование удобно проводить в программе «Живая геометрия».

Замок.

На рисунке изображён кодовый замок. Компания-производитель утверждает, что он очень надёжен, поскольку существует "несколько тысяч комбинаций". Правда ли это? Комбинацией является последовательность нажатий. При этом: одновременно можно нажать любое количество кнопок от 0 до 5, кнопки можно нажимать не более одного раза (можно ни разу). Примеры: 

{1, 2, 3}, {4, 5} – сначала нажали вместе 1, 2, 3, потом вместе 4 и 5; 

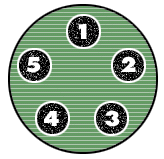{ 4, 5}, {1, 2, 3} – это другая комбинация, потому что порядок поменялся;

{1}, {3},{4, 5} ;

{1, 2, 3, 4, 5} (все кнопки сразу);

{1}, {3}, {2}, {5}, {4} (все кнопки по одной);

{} (ничего не нажали; дверь не заперта).

Игра Ним.

В игре Ним играют двое. Есть несколько кучек с камнями. За один ход можно взять любое количество камней, но только из одной кучки. Выигрывает тот игрок, который возьмет камни последним. Требуется разработать стратегию игры в Ним.

Это яркий пример темы, в которой помогать ученику можно очень по-разному. Можно дать формальное указание: «запиши количества камней в двоичной системе счисления, выравнивая их по правому края; докажи, что если все количества единиц в каждом столбце чётны, то позиция проигрышная», и т.д., которое для ученика будет взято «с потолка», даже если он всё это докажет. А можно дать способ найти эти закономерности самому. В этом и есть отличие «исследования» от «школьной задачи».

Огромный простор для исследования и изобретательности детского ума дают практико -ориентированные задачи.

Геометрические объекты существуют не только в математической теории но и в реальности. Приведу примеры таких задач:

1. Объяснить, почему стул на трех ножках устойчивее, чем на четырех ножках?

Как объяснить почему стулья в основном делают на четырех ножках, хотя они менее устойчивы.

1. Обычный стол на четырех ножках требуется внести из коридора в комнату,

прежде чем донести его до дверного проема, надо что-то измерить. Что именно?

3) Может ли существовать прямоугольник длиной 1 км, а площадью 1 мм²?

Таким образом, занимаясь исследованиями, в том числе и на уроках выпускник получит возможность научиться:

• самостоятельно планировать и выполнять учебное исследование;

• использовать догадку, озарение, интуицию,

• использовать такие математические приемы и методы, как перебор логических возможностей, математическое моделирование, доказательство по аналогии, доказательство от противного, опровержение, контрпример, индуктивные и дедуктивные рассуждения, построение и исполнение алгоритма.

Для того, чтобы учащиеся радовали нестандартными и красивыми предложениями и решениями, следует при планировании и проведении уроков стараться больше предоставлять им возможностей для самостоятельного мышления. Наблюдение за учениками, их мыслями, реакцией на события является неисчерпаемым источником вдохновения для учителя, прибавляющим сил для творчества - ведь совсем не хочется, чтобы наши ученики в школе, несмотря на то, что много читали и поверхностно рассуждали, много познавали, но при этом имели очень мало собственных мыслей.

Список литературы:

1. http://aga.org.uk/.

2. Алгебра: Учебник для 9 класса средней школы/ под ред.С.А.Теляковского.

3. 2-е изд.М.: Просвещение, 1992.270 раздел «Задачи повышенной сложности».