Сравнение рациональных чисел

Положительные и отрицательные числа

Повторение

- Приведите примеры положительных чисел.

- Приведите примеры отрицательных чисел.

- Чем отличаются друг от друга положительные и отрицательные числа?

- Что можно сказать про число 0?

- Как можно назвать все целые числа и все дроби?

Противоположные числа. Модуль числа.

- Дайте определение противоположных чисел и приведите примеры.

- Что называется модулем числа а?

- Чему равен модуль положительного числа? Пример.

- Чему равен модуль отрицательного числа? Пример.

- Чему равен модуль 0?

Задание 1.

Из чисел 13; -7.2; 0; 46; -46 выпишите :

а) положительные числа;

б) отрицательные числа;

в) число, которое не относится ни к положительным, ни к отрицательным .

Ответы:

а) 13; 46;

б) -7,2; -46;

в) 0.

Задание 2.

а) Запишите координаты отмеченных точек.

б) Отметьте на координатной прямой точки М(4); N(-3,5); Р(2,5); К(-2).

Ответы:

а) А (-2); В (1,5);

С (5); D (-4,5); О (0);

б)

Задание 3.

а) Запишите точки, которые имеют противоположные координаты.

б) Из данных чисел - 2,6; 2,05; 2,2;

-2,22; 2,53 выберите то, которое

имеет наибольший модуль.

в) Вычисли:

|-4| ∙ 1,5; 34 - |- 16|; |+23| + |-8|.

Ответы:

а) А (-3) и В (3);

б) -2,6;

в) 6; 18; 31.

Рефлексия:

• Кто думает, что материал предыдущих уроков усвоил хорошо?

• Кто считает, что надо ещё поработать над этим материалом?

- Кто удовлетворён своими результатами?

Тема урока:

Сравнение рациональных чисел

Сравните числа:

• Почему мы не можем сравнить последнюю пару чисел?
• - Как называются эти числа?
• - Все ли числа мы умеем сравнивать?

Цели обучения:

6.1.2.8 сравнивать целые числа.

Цели урока:

Учащиеся будут:

– знать понятие целого числа, отрицательного числа, рационального числа;

– уметь классифицировать числа;

– уметь изображать и сравнивать целые числа на координатной прямой;

– сравнение чисел на координатной прямой по их расположению содержательно – интуитивная часть;

– сравнение с помощью понятия модуля числа – формализованная часть.

Критерии оценивания:

– умеет изображать целые числа на координатной прямой;

– умеет сравнивать целые числа на координатной прямой по их расположению;

– умеет сравнивать целые числа с помощью понятия модуля числа.

Известно, что точка с меньшей координатной лежит на координатном луче левее точки с большой координатой.

Тогда: 01; 12; 23; 34; ...

На координатной прямой точно так же большее число изображается правее меньшего числа.

1. Увеличиваются или уменьшаются числа на координатной прямой в направлении от нуля влево? 2. Используя координатную прямую, сравните числа. Поставьте вместо звездочки знак так, чтобы получилось верное равенство. ( - 5) (- 4); ( - 4) (- 3); ( - 3) (- 2); ( - 2) (- 1); ( - 1) 0.

( - 5) (- 4); ( - 4) (- 3); ( - 3) (- 2); ( - 2) (- 1); ( - 1) 0.

Вчера температура воздуха была 2℃, а сегодня она понизилась и стала - 3℃. Сегодня было холоднее, чем вчера. Айман считает, что

– 3 меньше числа 2.

- 3

Считаете ли вы это правильно?

Поясните свой ответ.

Ответ: верно.

Так как - 3

Из двух точек на координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.

По изображению координатной прямой сравните числа координаты точки А(2) и В(6).

2

Правило нахождения расстояния между точками координатной прямой

Запомните!

Из двух положительных чисел больше то, у которого модуль больше.

По изображению координатной прямой сравните числа координаты точки А(2) и В(-5). .

- 5

Правило нахождения расстояния между точками координатной прямой

Запомните!

Любое положительное число больше нуля и больше любого отрицательного числа.

По изображению координатной прямой сравните числа координаты точки А(-1) и В(-5). .

-5

Правило нахождения расстояния между точками координатной прямой

Запомните!

Из двух отрицательных чисел больше то, у которого модуль меньше.

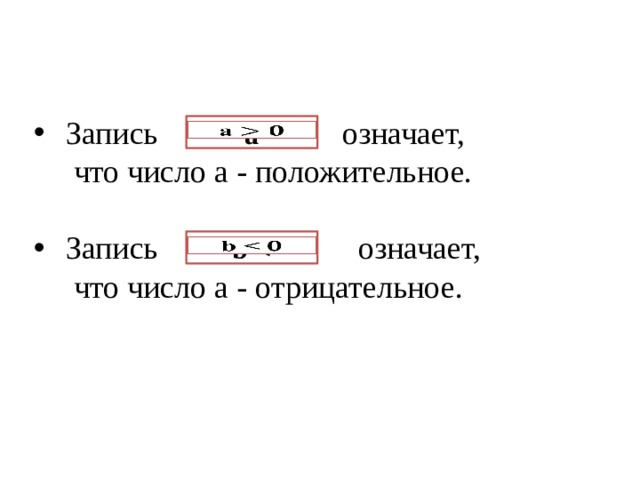
• Запись означает,

что число а - положительное.

• Запись означает,

что число а - отрицательное.

а

b

Шкала для самооценивания

 

Например:

• если вся работа сделана полностью, то ее можно оценить как «отлично»;
• если есть незначительные замечания с пояснениями к решениям, то работу можно оценить на «хорошо»:
• если около 70 всей работы выполнено правильно, то ее можно оценить как «необходимо больше практики»;

если решено менее 70 всей работы, то ее можно оценить как «нужна помощь».

Подведение итогов урока.

Групповая рефлексия

1. Сформулируйте цель, которая стояла перед вами.

2. Определите, достигнута ли цель.

3. Перечислите средства и способы, которые вам помогли достичь цели.

4. Сформулируйте неразрешённые затруднения на уроке, если они есть.

Индивидуальная рефлексия

Цель обучения

Знаю

сравнивать целые числа.

Получилось применить