Пояснительная записка.
Настоящая программа по математике для 6 класса создана на основе нормативных документов:
Федеральный компонент Государственного образовательного стандарта основного общего и среднего (полного) общего образования, утверждённого приказом МО от 5.03.2004 г. №1089.
Примерная программа основного общего образования по математике базового уровня, разработанной в соответствии со стандартом.
Место предмета в учебном плане: В учебном плане МОАУ «СОШ №67» на изучение математики в 6 классе отводится 5 часов в неделю, всего 175 часов.
Изучение математики в 6 классе направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Функции.
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
В ходе преподавания математики в 6 классе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обратить внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
работы с математическими моделями, приемами их построения и исследования;
методами исследования реального мира, умения действовать в нестандартных ситуациях;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи;
использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Тематическое планирование конкретизирует содержание предметных тем образовательного стандарта и дает поурочное распределение учебных часов.
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ
ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ
Натуральные числа. Степень с натуральным показателем. Делимость натуральных чисел. Признаки делимости на 2, 3, 5, 9, 10. Наибольший общий делитель и наименьшее общее кратное.
Дроби. Основное свойство дроби. Сравнение дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части.
Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной.
Рациональные числа. Целые числа: положительные, отрицательные и нуль. Модуль (абсолютная величина) числа. Сравнение рациональных чисел. Арифметические действия с рациональными числами.
Числовые выражения, порядок действий в них, использование скобок. Законы арифметических действий: переместительный, сочетательный, распределительный.
Текстовые задачи. Решение текстовых задач арифметическим способом.
Представление зависимости между величинами в виде формул.
Проценты. Нахождение процента от величины, величины по ее проценту.
Отношение, выражение отношения в процентах. Пропорция. Пропорциональная и обратно пропорциональная зависимости.
Округление чисел. Прикидка и оценка результатов вычислений.
Координаты. Изображение чисел точками координатной прямой. Формула расстояния между точками координатной прямой.
СОДЕРЖАНИЕ ПРОГРАММЫ
1. Повторение (18 ч)
Степень с натуральным показателем. Делимость натуральных чисел. Признаки делимости на 2, 3, 5, 9, 10. Наибольший общий делитель и наименьшее общее кратное.
Основная цель — завершить изучение натуральных чисел, подготовить основу для освоения действий с обыкновенными дробями.
В данной теме завершается изучение вопросов, связанных с натуральными числами. Основное внимание должно быть уделено знакомству с понятиями «делитель» и «кратное», которые находят применение при сокращении обыкновенных дробей и при их приведении к общему знаменателю. Упражнения полезно выполнять с опорой на таблицу умножения — прямым подбором.
Определенное внимание уделяется знакомству с признаками делимости, понятиям простого и составного чисел. При их изучении целесообразно формировать умения проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правило.
Учащиеся должны уметь разложить число на множители. Например, они должны понимать, что 36 = 6· 6 = 4· 9 = 2 ·18 и т. п. Умения разложить число на простые множители не обязательно добиваться от всех учащихся.
Основное свойство дроби. Сравнение дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части.
Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной.
Основная цель — выработать прочные навыки преобразования дробей, сложения и вычитания дробей.
Одним из важнейших результатов обучения является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведения к новому знаменателю. Умение приводить дроби к общему знаменателю используется для сравнения дробей.
При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Важно обратить внимание на случай вычитания дроби из целого числа.
Умножение и деление обыкновенных дробей. Основные задачи на дроби.
Основная цель — выработать прочные навыки арифметических действий с обыкновенными дробями и решения основных задач на дроби.
В этой теме завершается работа над формированием навыков арифметических действий с обыкновенными дробями. Навыки должны быть достаточно прочными, чтобы учащиеся не испытывали затруднений в вычислениях с рациональными числами, чтобы алгоритмы действий с обыкновенными дробями могли стать в дальнейшем опорой для формирования умений выполнять действия с алгебраическими дробями.
Расширение аппарата действий с дробями позволяет решать текстовые задачи, в которых требуется найти дробь от числа или число по данному значению его дроби.
2. Приближённые значения чисел (6 ч.)
Округление чисел. Прикидка и оценка результатов вычислений.
3. Среднее арифметическое чисел (4 ч.)
4. Дробные выражения (6 ч.)
5. Отношения и пропорции (23 ч)
Отношение, выражение отношения в процентах. Пропорция. Пропорциональная и обратно пропорциональная зависимости.
Основная цель — сформировать понятия пропорции, прямой и обратной пропорциональности величин.
Необходимо, чтобы учащиеся усвоили основное свойство пропорции, так как оно находит применение на уроках математики, химии, физики. В частности, достаточное внимание должно быть уделено решению с помощью пропорции задач на проценты.
Понятия о прямой и обратной пропорциональности величин можно сформировать как обобщение нескольких конкретных примеров, подчеркнув при этом практическую значимость этих понятий, возможность их применения для упрощения решения соответствующих задач.
В данной теме даются представления о длине окружности и площади круга. Соответствующие формулы к обязательному материалу не относятся. Рассмотрение геометрических фигур завершается знакомством с шаром.
6. Формулы. Прямая и обратная пропорциональные зависимости (7 ч.)
Решение текстовых задач арифметическим способом.
Представление зависимости между величинами в виде формул.
7. Длина окружности. Площадь круга (11 ч.)
8. Положительные и отрицательные числа (15 ч)
Целые числа: положительные, отрицательные и нуль. Модуль (абсолютная величина) числа.
Основная цель — расширить представления учащихся о числе путем введения отрицательных чисел.
Целесообразность введения отрицательных чисел показывается на содержательных примерах. Учащиеся должны научиться изображать положительные и отрицательные числа на координатной прямой. В дальнейшем она будет служить наглядной основой для правил сравнения чисел, сложения и вычитания чисел.
Специальное внимание должно быть уделено усвоению вводимого здесь понятия модуля числа, прочное знание которого необходимо для формирования умения сравнивать отрицательные числа, а в дальнейшем и для овладения алгоритмами арифметических действий с положительными и отрицательными числами.
9. Сравнение рациональных чисел (6 ч) Сравнение рациональных чисел
10. Сложение и вычитание положительных и отрицательных чисел (16 ч)
.Арифметические действия с рациональными числами.
Основная цель — выработать прочные навыки сложения и вычитания положительных и отрицательных чисел.
Действия с отрицательными числами вводятся на основе представлений об изменении величин: сложение и вычитание чисел иллюстрируется соответствующими перемещениями точек координатной прямой. При изучении данной темы отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами.
11. Умножение и деление положительных и отрицательных чисел (12 ч)
Арифметические действия с рациональными числами.
Умножение и деление положительных и отрицательных чисел. Понятие о рациональном числе. десятичное приближение обыкновенной дроби. Применение законов арифметических действий для рационализации вычислений.
Основная цель — выработать прочные навыки арифметических действий с положительными и отрицательными числами.
Навыки умножения и деления положительных и отрицательных чисел отрабатываются сначала при выполнении отдельных действий, а затем в сочетании с навыками сложения и вычитания при вычислении значений числовых выражений.
При изучении данной темы учащиеся должны усвоить, что для обращения обыкновенной дроби в десятичную достаточно разделить (если это возможно) числитель на знаменатель. В каждом конкретном случае они должны знать, в какую дробь обращается данная обыкновенная дробь — в десятичную или периодическую. Учащиеся должны знать представление в виде десятичной дроби таких дробей, как
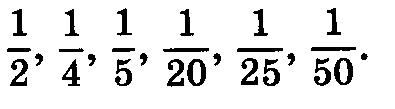
12. Преобразование числовых и буквенных выражений (13 ч)
Числовые выражения, порядок действий в них, использование скобок. Законы арифметических действий: переместительный, сочетательный, распределительный.
13. Решение уравнений (11 ч)
Простейшие преобразования выражений: раскрытие скобок, приведение подобных слагаемых. Решение линейных уравнений. Примеры решения текстовых задач с помощью линейных уравнений.
Основная цель — подготовить учащихся к выполнению преобразований выражений, решению уравнений.
Преобразования буквенных выражений путем раскрытия скобок и приведения подобных слагаемых отрабатываются в той степени, в которой они необходимы для решения несложных уравнений.
Введение арифметических действий над отрицательными числами позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одной переменной.
14. Координатная плоскость (10 ч)
Изображение чисел точками координатной прямой. Формула расстояния между точками координатной прямой.
Основная цель — познакомить учащихся с прямоугольной системой координат на плоскости.
Учащиеся должны научиться распознавать и изображать перпендикулярные и параллельные прямые. Основное внимание следует уделить отработке навыков их построения с помощью линейки и чертежного треугольника, не требуя воспроизведения точных определений.
Основным результатом знакомства учащихся с координатной плоскостью должны стать знания порядка записи координат точек плоскости и их названий, умения построить координатные оси, отметить точку по заданным координатам, определить координаты точки, отмеченной на координатной плоскости.
Формированию вычислительных и графических умений способствует построение столбчатых диаграмм. При выполнении соответствующих упражнений найдут применение изученные ранее сведения о масштабе и округлении чисел.
15. Повторение. Решение задач (17 ч)
Решение текстовых задач арифметическим способом.
Требования к уровню подготовки обучающихся. В результате изучения математики ученик должен
знать/понимать1
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь — в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
Критерии нормы оценки знаний, умений и навыков учащихся по математике.
Оценка устного ответа
Отметка «5»
ответ полный и правильный на основании изученного материала;
материал изложен в определенной логической последовательности, литературным языком;
ответ самостоятельный.
Отметка «4»
ответ полный и правильный на основании изученного материала;
материал изложен в определенной логической последовательности, при этом допущены две-три несущественные ошибки, исправленные по требованию учителя.
Отметка «3»
Отметка «2»
- при ответе обнаружено непонимание учащимся основного содержания учебного материала или допущены существенные ошибки, которые учащийся не может исправить при наводящих вопросах учителя.
Отметка «2» отмечает такие недостатки в подготовке ученика, которые являются серьезным препятствием к успешному овладению последующим материалом.
Отметка («5», «4», «3») может ставиться не только за единовременный ответ (когда на проверку подготовки ученика отводится определенное время), но и за рассредоточенный во времени, т.е. сумму ответов, данных учеником на протяжении урока (выводится поурочный балл), при условии, если в процессе урока не только заслушивались ответы учащегося, но и осуществлялась проверка его умения применять полученные знания.
при проверке письменных контрольных и самостоятельных работ
Оценка "5"
Оценка "5" ставится:
а) работа выполнена полностью и без ошибок;
б) количество недочетов в такой работе не должно превышать двух.
Оценка "4"
Оценка "4" ставится:
а) работа выполнена полностью, но содержит не более 3-4 недочетов;
б) из всех предложенных заданий не выполнено одно задание;
в) содержит одну грубую ошибку.
Оценка "3"
Оценка "3" ставится:
а) выполнено верно половина из всех предложенных заданий
б) работа содержит не более 5-7 недочетов.
Оценка "2"
Оценка "2" ставится во всех остальных случая
Грубые ошибки.
К грубым ошибкам относятся ошибки, которые обнаруживают незнание учащимися формул, правил, основных свойств, теорем и неумение их применять, незнание приемов решения задач, рассматриваемых в учебных пособиях, а также вычислительные ошибки, если он не являются опиской.
Негрубые ошибки.
К негрубым ошибкам относятся:
- потеря корня или сохранение в ответе постороннего корня;
- отбрасывание без объяснения одного из корня и равнозначные им.
К недочетам относятся:
- нерациональное решение, описки, недостаточность;
- отсутствие пояснений, обоснований в решениях.
Если одна и та же ошибка (один и тот же недочет) встречаются несколько раз, то это рассматривается как одна ошибка (один недочет).
Зачеркивание в работе (желательно, чтобы они были аккуратными) свидетельствует о поисках решения, что считать ошибкой не следует.
Описание учебно-методического и материально-технического обеспечения
Для реализации целей и задач обучения математике по данной программе используется УМК по математике для 5-6классов Н.Б. Истомина
авторов
Н.Б. Истомина. Учебник для 6 класса общеобразовательных учреждений – 6-е изд., испр. и доп. – Смоленск: «Ассоциация ХХI век», 2008. – 208 с.
Истомина Н.Б., Редько З.Б. Уроки математики: 6 класс. Содержание курса. Планирование уроков. Методические рекомендации: пособие для учителей. – Смоленск: «Ассоциация ХХI век», 2007. – 224 с.
Истомина Н.Б., Горина О.П. Контрольные работы по математике. 6 класс - Смоленск: «Ассоциация ХХI век», 2006. – 64 с.
К техническим средствам обучения, которые могут эффективно использоваться на уроках математики, относятся компьютер, интерактивная доска.
Технические средства на уроках математики широко привлекаются также при подготовке проектов (компьютер)
Литература:
Н.Б. Истомина. Учебник для 6 класса общеобразовательных учреждений – 6-е изд., испр. и доп. – Смоленск: «Ассоциация ХХI век», 2008. – 208 с.
Истомина Н.Б., Редько З.Б. Уроки математики: 6 класс. Содержание курса. Планирование уроков. Методические рекомендации: пособие для учителей. – Смоленск: «Ассоциация ХХI век», 2007. – 224 с.
Истомина Н.Б., Горина О.П. Контрольные работы по математике. 6 класс - Смоленск: «Ассоциация ХХI век», 2006. – 64 с.
Тематическое планирование по математике 6 класс
| № п/п | № урока | Тема урока | Обязательный минимум по стандарту | Основные виды деятельности обучающихся | Повторение |
Дата проведения
|
| 6А
| 6Б
|
| Глава 1. Обыкновенные и десятичные дроби |
|
| §1. Проверь себя! Чему ты научился в 5 классе? (18 часов) |
|
| 1 | 1 | Наибольший общий делитель и наименьшее общее кратное. | Разложение натурального числа на простые множители. Наибольший общий делитель и наименьшее общее кратное. | Формулировать определения понятий «кратное», «делитель», «общее кратное», «наименьшее общее кратное», «общий делитель», «наибольший общий делитель», иллюстрировать их и применять в речи. Находить наименьшее общее кратное и наибольший общий делитель двух чисел, использовать соответствующие обозначения. Решать текстовые задачи, связанные с делимостью чисел. | Признаки делимости числа. Степень числа | 1.09. | 1.09. |
| 2 | 2 | Признаки делимости на 2, 3, 5, 9, 10.. Степень с натуральным показателем.
| Степень с натуральным показателем. | Свойства делимости суммы, разности, произведения. Решение задач | 2.09. | 2.09. |
| 3 | 3 | Делимость натуральных чисел. Свойства делимости суммы, разности, произведения. Решение задач | Делимость натуральных чисел. | Уравнение. Корень уравнения. | 3.09 | 3.09 |
| 4 | 4 | Решение уравнений. Двойное неравенство. Координатный луч. | Уравнение с одной переменной. Корень уравнения. Изображение чисел точками координатной прямой. |
| 4.09 | 4.09 |
| 7.09 | 7.09 |
| 5 | 5 | Решение уравнений. Двойное неравенство. Координатный луч. |
| 6 | 6 | Основное свойство дроби. Сокращение дробей. Сравнение обыкновенных дробей. | Обыкновенная дробь. Основное свойство дроби. Сравнение дробей. | Формулировать, записывать с помощью букв основное свойство обыкновенной дроби, правила действий с обыкновенными дробями. Преобразовывать обыкновенные дроби, сравнивать и упорядочивать их. Выполнять вычисления с обыкновенными дробями. | Дробь. | 8.09 | 8.09 |
| 7 | 7 | Основное свойство дроби. Сокращение дробей. Сравнение обыкновенных дробей.
| 10.09 | 10.09 |
| 8 | 8 | Арифметические действия с обыкновенными дробями. | Арифметические действия с обыкновенными дробями.
| Арифметические действия с обыкновенными дробями. | 11.09
| 11.09
|
| 14.09 | 14.09 |
| 9 | 9 | Арифметические действия с обыкновенными дробями. |
| 10 | 10 | Нахождение части от целого и целого по его части. | Нахождение части от целого и целого по его части.
|
| 15.09 | 15.09 |
| 11 | 11 | Нахождение части от целого и целого по его части. | 16.09 | 16.09 |
| Записывать и читать десятичные дроби. Представлять обыкновенные дроби в виде десятичных и десятичные в виде обыкновенных. Сравнивать и упорядочивать десятичные дроби. Выполнять вычисления с десятичными дробями. |
| 12 | 12 | Арифметические действия с десятичными дробями. | Десятичная дробь. Сравнение десятичных дробей. Арифметические действия с десятичными дробями
| Арифметические действия с десятичными дробями. | 17.09 | 17.09 |
| 13 | 13
| Арифметические действия с десятичными дробями. | 18.09
| 18.09
|
| 14 | 14 | Проценты. Нахождение процента от величины, величины по ее проценту.
| Объяснять, что такое процент. Представлять проценты в дробях и дроби в процентах. Решать задачи на проценты и дроби( в том числе задачи из реальной практики) | Процент. Правила нахождения целого по части и части по целому. | 21.09 | 21.09 |
| Нахождение части от целого и целого по его части.
|
| 15 | 15 | Проценты. Нахождение процента от величины, величины по ее проценту.
| 22.09 | 22.09 |
| 16 | 16 | Решение задач на повторение. Подготовка к контрольной работе | Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, моделировать условие с помощью схем, рисунков. |
| 23.09 | 23.09 |
| 17 | 17 | Контрольная работа № 1 (входная) |
|
| 24.09 | 24.09 |
| 18 | 18 | Анализ контрольной работы № 1. |
|
| 25.09 | 25.09 |
| §2. Приближённые значения чисел (6 часов) |
| 19 | 1 | Округление чисел. Прикидка и оценка результатов вычислений.
| Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной |
|
| 28.09 | 28.09 |
| 20 | 2 | Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной. | Использовать эквивалентные представления дробных чисел. Выполнять прикидку и оценку в ходе вычислений. | Перевод обыкновенных дробей в десятичные дроби. | 29.09 | 29.09 |
| 21 | 3 | Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной. | 30.09 | 30.09 |
| 22 | 4 | Применение правил округления чисел
| Округление чисел. Прикидка и оценка результатов вычислений. |
| 1.10 | 1.10 |
| 2.10 | 2.10 |
| 23 | 5 | Применение правил округления чисел
|
| 24 | 6 | Самостоятельная работа № 1 «Округление чисел» |
|
| 5.10 | 5.10 |
| §3. Среднее арифметическое чисел (4 часа) |
| 25 | 1 | Правило нахождения среднего арифметического чисел | Арифметические действия с десятичными дробями | Объяснять, что такое среднее арифметическое. Находить среднее арифметическое двух и более чисел. | Сложение натуральных и дробных чисел | 6.10 | 6.10 |
| 26 | 2 | Применение правила нахождения среднего арифметического чисел | 7.10 | 7.10 |
| 27 | 3 | Применение правила нахождения среднего арифметического чисел | 8.10 | 8.10 |
| 28 | 4 | Самостоятельная работа № 2 «Среднее арифметическое чисел» |
|
| 9.10 | 9.10 |
| §4. Дробные выражения (6 часов) |
| 29 | 1 | Понятие «дробное выражение» | Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной | Выполнять вычисления с обыкновенными дробями. Выполнять вычисления с десятичными дробями. | Дробь | 12.10 | 12.10 |
| 30 | 2 | Преобразование дробных выражений | Действия с дробями | 13.10 | 13.10 |
| 31 | 3 | Преобразование дробных выражений | 14.10 | 14.10 |
| 32 | 4 | Преобразование дробных выражений | 15.10 | 15.10 |
| 33 | 5 | Контрольная работа № 2 «Числовые выражения» |
|
| 16.10 | 16.10 |
| 34 | 6 | Анализ контрольной работы № 2. |
|
| 19.10 | 19.10 |
| §5. Отношения (13 часов) |
| 35 | 1 | Смысл понятия «отношение» | Отношение, выражение отношения в процентах.
| Формулировать определение отношения чисел. Понимать и объяснять, что показывает отношение двух чисел. Составлять отношения, объяснять содержательный смысл составленного отношения, используя стандартные обороты речи со словом «отношение». Решать задачи на деление чисел и величин в данном отношении, в том числе задачи практического характера, задачи, связанные с нахождением точки на координатной прямой по заданному отношению и координатам двух точек. Формулировать определение пропорции, иллюстрировать его на примерах; грамотно читать равенство, записанное в виде пропорции. Называть крайние и средние члены пропорции. Формулировать основное свойство пропорции и обратное ему утверждение. Иллюстрировать их на примерах, применять при составлении и решении пропорций. |
| 20.10 | 20.10 |
| 36 | 2 | Упрощение отношений | Отношение. | 21.10 | 21.10 |
| 37 | 3 | Упрощение отношений | 22.10 | 22.10 |
| 38 | 4 | Отношение, выражение отношения в процентах | Нахождение процента | 23.10 | 23.10 |
| 39 | 5 | Отношение, выражение отношения в процентах | 26.10 | 26.10 |
| 40 | 6 | Решение задач |
Нахождение части от целого и целого по его части. |
| Нахождение процента | 27.10 | 27.10 |
| 41
| 7 | Решение задач | Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, осуществлять самоконтроль, проверяя ответ на соответствие. Составлять задачи по заданной математической модели. | 28.10 | 28.10 |
| 42 | 8 | Подготовка к контрольной работе |
|
| 29.10 | 29.10 |
| 43 | 9 | Итоговая контрольная работа за I четверть (№ 3) |
|
| 30.10 | 30.10 |
| 44 | 10 | Анализ контрольной работы № 3 |
|
|
|
|
| 45 | 11 | Взаимосвязь понятий «отношение» и «масштаб». Решение задач
| Отношение, выражение отношения в процентах.
| Пользоваться понятием «масштаб», решать задачи, используя понятия «масштаб», «отношение», «процент» | Отношение. Масштаб. |
|
|
| 46 | 12 | Взаимосвязь понятий «отношение» и «масштаб». Решение задач
|
|
|
| 47 | 13 | Взаимосвязь понятий «отношение» и «масштаб». Решение задач |
|
|
| §5. Отношения (продолжение) (2 часа) |
| 48 | 1 | Решение задач «Отношение и масштаб».
| Отношение, выражение отношения в процентах.
| Решать задачи, используя понятия «масштаб», «отношение», «процент» | Отношение. Масштаб. |
|
|
| 49 | 2 |
Решение задач «Отношение и масштаб». |
|
|
|
|
| §6. Пропорции (8 часов) |
| 50 | 1 | Пропорция. | Пропорция.
| Составлять пропорции, находить неизвестный член пропорции. Использовать понятие «пропорция» при решении уравнений и текстовых задач. | Отношение, дробь |
|
|
| 51 | 2 | Основное свойство пропорции
|
|
|
|
| 52 | 3 | Применение понятия «пропорция» для решения уравнений, составление новых пропорций из данных |
|
|
|
| 53 | 4 | Применение знаний о пропорциях
| Решать текстовые задачи с помощью пропорции, основного свойства пропорции. Анализировать и осмысливать текст задачи, выполнять краткую запись к условию задачи на прямую и обратную пропорциональность, составлять на основании записи уравнение, решать его, оценивать ответ на соответствие. Решать с помощью пропорций задачи геометрического содержания, задачи на проценты. | Отношение. Пропорция. Основное свойство пропорции. |
|
|
|
|
|
| 54 | 5 | Применение знаний о пропорциях
|
|
|
|
| 55 | 6 | Применение знаний о пропорциях
|
| 56 | 7 | Контрольная работа № 4 «Пропорции» |
|
|
|
|
| 57 | 8 | Анализ контрольной работы № 4 |
|
|
|
|
| §7. Формулы. Прямая и обратная пропорциональная зависимость (7 часов) |
| 58 | 1 | Пропорциональная и обратно пропорциональная зависимости. | Единицы измерения длины, площади, объема, массы, времени, скорости. Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. Пропорциональная и обратно пропорциональная зависимости. | Выражать одни единицы измерения величины в других единицах (метры в километрах, минуты в часах и т.п.). Моделировать несложные зависимости с помощью формул; выполнять вычисления по формулам. Использовать знания о зависимостях между величинами( скорость, время, расстояние; работа, производительность, время и т.п.) | Известные формулы |
|
|
| 59 | 2 | Пропорциональная и обратно пропорциональная зависимости. |
|
|
|
| 60 | 3 | Составление пропорций | Понятие «обратно пропорциональная зависимость» и «прямо пропорциональная зависимость» |
|
|
| 61 | 4 | Применение понятий прямо пропорциональной зависимости и обратно пропорциональной зависимости при решении задач | Понимать и верно использовать в речи термины: пропорциональные (прямо пропорциональные) величины, обратно пропорциональные величины, попарно пропорциональные величины. Формулировать отличие прямо и обратно пропорциональных величин. Приводить примеры величин, находящихся в прямо пропорциональной зависимости, обратно пропорциональной зависимости, комментировать примеры. Определять по условию задачи, какие величины являются прямо пропорциональными, обратно пропорциональными, а какие не являются ни теми, ни другими. Решать задачи на прямую и обратную пропорциональность. | Понятие «обратно пропорциональная зависимость» и «прямо пропорциональная зависимость» |
|
|
|
|
|
| 62 | 5 | Применение понятий прямо пропорциональной зависимости и обратно пропорциональной зависимости при решении задач
|
|
|
|
| 63 | 6 | Применение понятий прямо пропорциональной зависимости и обратно пропорциональной зависимости при решении задач |
| 64 | 7 | Самостоятельная работа № 3 «Формулы. Пропорциональные зависимости» |
|
|
|
|
| §8. Длина окружности. Площадь круга (11 часов) |
| 65 | 1 | Формула длины окружности | Представление зависимости между величинами в виде формул. Решение текстовых задач арифметическим способом.
Решение текстовых задач арифметическим способом.
| Понимать и использовать терминологию, связанную с окружностью. Находить экспериментальным путём отношение длины окружности к диаметру. Определять длину окружности по готовому рисунку. Использовать формулу длины окружности при решении практических задач. Находить с помощью циркуля и линейки центр окружности, если он не обозначен, используя свойство прямого угла или свойство серединного перпендикуляра. Анализировать задания, аргументировать и презентовать решения. Находить информацию по заданной теме в источниках различного типа. Использовать компьютерное моделирование и эксперимент для изучения свойств окружности. Понимать и использовать терминологию, связанную с окружностью, кругом. Исследовать и выводить по заданному алгоритму формулу площади круга. Определять по готовому рисунку площадь круга, площадь комбинированных фигур. Использовать формулу площади круга при решении практических задач. | Окружность |
|
|
| 66 | 2 | Представление зависимости между величинами в виде формул. | Формула длины окружности |
|
|
|
|
|
| 67 | 3 | Решение задач
|
| 68 | 4 | Решение задач
|
|
|
|
| 69
| 5 | Формула площади круга | Круг |
|
|
| 70 | 6 | Решение задач
| Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, моделировать условие с помощью схем, рисунков. | Формула площади круга |
|
|
| 71 | 7 | Решение задач |
|
|
|
| 72 | 8 | Самостоятельная работа № 4 «Круг и окружность» |
|
|
|
|
| 73 | 9 | Диаграммы |
| Круг, окружность. |
|
|
| 74 | 10 | Контрольная работа № 5 «Круг и окружность» |
|
|
|
|
| 75 | 11 | Анализ контрольной работы № 5 |
|
|
|
|
| Глава II. Рациональные числа |
| §1. Положительные и отрицательные числа (2 часа) |
| 76 | 1 | Целые числа: положительные, отрицательные и нуль. | Целые числа: положительные, отрицательные и нуль. | Приводить примеры использования в окружающем мире положительных и отрицательных чисел (температура, выигрыш – проигрыш, выше - ниже уровня моря и т.п.) | Натуральные и дробные числа |
|
|
| 77 | 2 | Целые числа: положительные, отрицательные и нуль. |
|
|
| §2. Координатная прямая (1 час) |
| 78 | 1 | Координатная прямая | Изображение чисел точками координатной прямой. | Строить координатную прямую по алгоритму (прямая, с указанными на ней началом отсчёта, направлением отсчёта, и единичным отрезком). Изображать положительные и отрицательные числа точками координатной прямой. Выполнять обратную операцию. Понимать и применять в речи термины: координатная прямая, координата точки на прямой, положительное число, отрицательное число. Анализировать задания, аргументировать и презентовать решения. | Координатный луч |
|
|
| §3. Противоположные числа. Модуль числа (5 часов) |
| 79 | 1 | Противоположные числа |
Этапы развития представления | Объяснять, какие числа называются противоположными. Записывать число, противоположное данному с помощью знака (–). Объяснять смысл записей (– а), –(– а). Объяснять смысл равенства –(– а) = а, применять его. Находить число, противоположное данному числу. |
|
|
|
| 80 | 2 | Координатная прямая, отрицательные числа | Координатный луч |
|
|
| 81 | 3 | Модуль (абсолютная величина) числа. | Модуль (абсолютная величина) числа. | Усвоить понятие «модуль» числа. | Расстояние до точки на координатном луче |
|
|
| 82 | 4 | Итоговая контрольная работа за II четверть (№ 6) |
|
|
|
|
| 83 | 5 | Анализ контрольной работы № 6 |
|
|
|
|
| §3. Противоположные числа. Модуль числа (продолжение)(7 часов) |
| 84 | 1 | Модуль (абсолютная величина) числа. | Модуль (абсолютная величина) числа. | Понимать и применять геометрический смысл понятия модуля числа. Находить модуль данного числа. Выполнять арифметические примеры, содержащие модуль, комментировать решения. | Расстояние до точки на координатном луче |
|
|
|
|
|
| 85 | 2 | Модуль (абсолютная величина) числа. |
| 86 | 3 | Решение задач
| Решение текстовых задач арифметическим способом. | Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, моделировать условие с помощью схем, рисунков. |
|
|
|
| 87 | 4 | Решение задач
|
|
|
|
|
|
| 88 | 5 | Решение задач
|
| 89 | 6 | Контрольная работа № 7 «Противоположные числа. Модуль числа» |
|
|
|
|
|
| 90 | 7 | Анализ контрольной работы № 7 |
|
|
|
|
|
| §4. Сравнение рациональных чисел (6 часов) |
| 91 | 1 | Правило сравнения отрицательных чисел | Сравнение рациональных чисел.
Модуль (абсолютная величина) числа. Сравнение рациональных чисел.
| Сравнивать с помощью координатной прямой: положительное число и нуль; отрицательное число и нуль; положительное и отрицательное числа; два отрицательных числа. Моделировать с помощью координатной прямой отношения «больше» и «меньше» для рациональных чисел. Понимать и применять в речи термины: противоположные числа, целое число, модуль числа, неотрицательные числа, неположительные числа. Анализировать задания, аргументировать и презентовать решения. | Сравнение натуральных и дробных чисел |
|
|
| 92 | 2 | Сравнение рациональных чисел |
|
|
| 93 | 3 | Сравнение рациональных чисел |
|
|
| 94 | 4 | Сравнение модулей |
|
|
|
| 95 | 5 | Модуль числа. Противоположные числа. Сравнение рациональных чисел | Модуль. |
|
|
| 96 | 6 | Самостоятельная работа № 5 «Сравнение рациональных чисел» |
|
|
|
|
| §5. Сложение и вычитание рациональных чисел (16 часов) |
| 97 | 1 | Правило сложения рациональных чисел с одинаковыми знаками | Арифметические действия с рациональными числами.
| Формулировать и записывать с помощью букв свойства действий с рациональными числами. Выполнять вычисления с рациональными числами. | Сложение и вычитание натуральных чисел, свойства сложения и вычитания |
|
|
| 98 | 2 | Правило сложения рациональных чисел с одинаковыми знаками |
|
|
| 99 | 3 | Правило сложения рациональных чисел с разными знаками |
|
|
| 100 | 4 | Правило сложения рациональных чисел с разными знаками |
|
|
| 101 | 5 | Сложение рациональных чисел | Сложение рациональных чисел |
|
|
| 102 | 6 | Переместительное и сочетательное свойства сложения |
|
|
|
| 103 | 7 | Вычитание рациональных чисел | Сложение рациональных чисел. |
|
|
| 104 | 8 | Вычитание рациональных чисел |
|
|
|
| 105 | 9 | Алгебраическая сумма | Арифметические действия с рациональными числами.
| Формулировать определение алгебраической суммы. Аргументировать с помощью конкретных примеров справедливость переместительного и сочетательного законов арифметических действий для суммы положительных и отрицательных чисел. Распознавать алгебраическую сумму и её слагаемые. Представлять алгебраическую сумму в виде суммы положительных и отрицательных чисел, находить её рациональным способом. Вычислять значения буквенных выражений при заданных значениях букв. Анализировать задания, аргументировать и презентовать решения. | Запись суммы чисел |
|
|
| 106 | 10 | Запись алгебраической суммы и вычисление её значения |
|
|
| 107 | 11 | Формула расстояния между точками координатной прямой. | Изображение чисел точками координатной прямой. Геометрический смысл модуля числа. Формула расстояния между точками координатной прямой.
| Проводить по алгоритму простейшие исследования для определения расстояния между точками координатной прямой. Формулировать правило нахождения расстояния между точками по заданным координатам этих точек. Записывать, грамотно читать и применять в различных ситуациях формулу нахождения расстояния между двумя точками ρ(а; в) = |a – b|. Излагать информацию, интерпретируя факты, разъясняя значение и смысл теории. | Модуль числа |
|
|
| 108 | 12 | Арифметические действия с рациональными числами. | Арифметические действия с рациональными числами.
| Формулировать и записывать с помощью букв свойства действий с рациональными числами. Понимать геометрический смысл сложения рациональных чисел. Объяснять нахождение суммы чисел на примерах перемещения точки вдоль координатной прямой, изменения температуры, а так же с использованием понятий «прибыль» и «долг», «доход» и «расход». Моделировать с помощью координатной прямой сложение рациональных чисел. Анализировать задания, аргументировать и презентовать решения. | Правила сложения и вычитания рациональных чисел. |
|
|
| 109 | 13 | Арифметические действия с рациональными числами. |
|
|
|
|
|
| 110 | 14 | Арифметические действия с рациональными числами. |
| 111 | 15 | Контрольная работа № 8 «Сложение и вычитание рациональных чисел» |
|
|
|
|
| 112 | 16 | Анализ контрольной работы № 8. |
|
|
|
|
| §6. Умножение и деление рациональных чисел (12 часов) |
| 113 | 1 | Правила умножения рациональных чисел | Арифметические действия с рациональными числами.
| Формулировать, обосновывать, иллюстрировать примерами и применять правила умножения числа на 1 и на (– 1). Формулировать, иллюстрировать примерами правила умножения и деления двух чисел с разными знаками. Формулировать, иллюстрировать примерами правила умножения и деления двух чисел с одинаковыми знаками. Применять эти правила при умножении и делении на целое число и десятичную дробь. Формулировать, иллюстрировать примерами и применять распределительный закон умножения. Исследовать влияние смены знаков в сомножителях на результат. | Умножение и деление, правила умножения и деления |
|
|
| 114 | 2 | Выполнение умножения рациональных чисел |
|
|
| 115 | 3 | Выполнение умножения рациональных чисел
|
|
|
|
|
|
| 116 | 4 | Выполнение умножения рациональных чисел |
| 117 | 5 | Правила деления рациональных чисел | Выполнение умножения рациональных чисел
|
|
|
| 118 | 6 | Замена знаков в отрицательной дроби | Числитель и знаменатель дроби. |
|
|
| 119 | 7
| Выполнение делений рациональных чисел | Деление обыкновенных и десятичных дробей. |
|
|
| 120 | 8 | Выполнение делений рациональных чисел
|
|
|
|
|
|
| 121 | 9 | Выполнение делений рациональных чисел |
| 122 | 10 | Арифметические действия с рациональными числами. |
|
|
| 123 | 11 | Контрольная работа № 9 «Умножение и деление рациональных чисел» |
|
|
|
|
| 124 | 12 | Анализ контрольной работы № 9 |
|
|
|
|
| §7. Преобразование числовых и буквенных выражений (13 часов) |
| 125 | 1 | Правила раскрытия скобок | Числовые выражения, порядок действий в них, использование скобок. Законы арифметических действий: переместительный, сочетательный, распределительный.
Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. | Читать и записывать буквенные выражения, составлять буквенное выражение по условию задачи. Вычислять числовое значение буквенного выражения при заданных значениях букв.
Применять правила раскрытия скобок для преобразования числовых и буквенных выражений. | Свойства сложения и умножения натуральных чисел, раскрытие скобок в выражении. Подобные слагаемые. |
|
|
| 126 | 2 | Числовые выражения, порядок действий в них, использование скобок. |
|
|
| 127 | 3 | Числовые выражения, порядок действий в них, использование скобок. |
|
|
| 128 | 4 | Приведение подобных слагаемых.
|
|
|
|
|
|
| 129 | 5
| Приведение подобных слагаемых.
|
| 130 | 6 | Правила раскрытия скобок и приведение подобных слагаемых
|
|
|
|
|
|
| 131 | 7 | Правила раскрытия скобок и приведение подобных слагаемых
|
| 132 | 8 | Законы арифметических действий: переместительный, сочетательный, распределительный. | Подобные слагаемые, правила раскрытия скобок. |
|
|
| 133 | 9 | Законы арифметических действий: переместительный, сочетательный, распределительный. |
|
|
| 134 | 10 | Решение задач способом составления уравнений | Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, моделировать условие с помощью схем, рисунков. | Решение текстовых задач |
|
|
| 135 | 11 | Решение задач способом составления уравнений |
|
|
|
|
| 136 | 12 | Контрольная работа № 10 «Преобразование числовых и буквенных выражений» |
|
|
|
|
| 137 | 13 | Анализ контрольной работы № 10 |
|
|
|
|
| §8. Решение уравнений (11 часов) |
| 138 | 1 | Алгебраический способ решения уравнений
| Уравнение с одной переменной. Корень уравнения. Линейное уравнение. | Понимать и применять в речи термины: переменная величина (переменная), постоянная величина (постоянная), взаимное уничтожение слагаемых. Исследовать способы решения уравнений. Формулировать для каждого из способов алгоритм решения уравнений. Формулировать алгоритм решения уравнений алгебраическим способом. Решать простейшие уравнения алгебраическим способом, используя перенос слагаемых из одной части уравнения в другую.
| Решение уравнений |
|
|
|
|
|
| 139 | 2 | Алгебраический способ решения уравнений
|
| 140 | 3 | Преобразование уравнений
| Правила раскрытия скобок. |
|
|
| 141 | 4 | Преобразование уравнений
|
|
|
| 142 | 5 | Преобразование уравнений
|
|
|
| 143 | 6 | Решение задач способом составления уравнений
| Решение текстовых задач |
|
|
| Понимать и использовать в речи терминологию: математическая модель реальной ситуации, работа с математической моделью. Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, осуществлять самоконтроль, проверяя ответ на соответствие. Составлять задачи по заданной математической модели. |
|
|
|
| 144 | 7 | Решение задач способом составления уравнений
|
|
|
|
| 145 | 8 | Решение задач способом составления уравнений
|
|
|
|
| 146 | 9 | Решение задач способом составления уравнений
|
| 147 | 10 | Контрольная работа № 11 «Решение уравнений» |
|
|
|
|
| 148 | 11 | Анализ контрольной работы № 11 |
|
|
|
|
| §9. Координатная плоскость (10 часов) |
| 149 | 1 | Координатная плоскость. Ось абсцисс. Ось ординат | Декартовы координаты на плоскости; координаты точки. | Объяснять и иллюстрировать понятия: система координат, координатные прямые, начало координат, ось абсцисс, ось ординат, координатная плоскость, координаты точки на плоскости. Строить на координатной плоскости точки и фигуры по заданным координатам, находить координаты точек. Проводить исследования, связанные с взаимным расположением точек на координатной плоскости. Понимать и применять в речи соответствующие термины и символику. Показывать на координатной плоскости расположение точек с равными абсциссами, с равными ординатами. Находить по трём вершинам с заданными координатами координаты четвёртой вершины прямоугольника. Анализировать задания, аргументировать и презентовать решения. | Координатная прямая |
|
|
| 150 | 2 | Изображение чисел точками координатной прямой. | Координаты точек на прямой |
|
|
|
|
|
| 151 | 3 | Изображение чисел точками координатной прямой. |
|
|
|
| 152 | 4 | Изображение чисел точками координатной прямой. |
| 153 | 5 | Координатные четверти | Координатная плоскость. |
|
|
| 154 | 6 | Координатная плоскость. Графики |
|
|
|
| 155 | 7 | Чтение и построение графиков
| Моделировать реальные зависимости с помощью формул и графиков. Интерпретировать графики реальных зависимостей. | Координата точки, координатные четверти. |
|
|
|
|
|
| 156 | 8 | Чтение и построение графиков
|
| 157 | 9 | Контрольная работа № 12 «Координатная плоскость» |
|
|
|
| 158 | 10 | Анализ контрольной работы № 12 |
|
|
|
|
| §10. Проверь себя! Чему ты научился в шестом классе? (10 часов) |
| 159 | 1 | Отношения и пропорции | Отношение, выражение отношения в процентах. Пропорция. Пропорциональная и обратно пропорциональная зависимости.
| Решать текстовые задачи с помощью пропорции, основного свойства пропорции. | Действия с рациональными числами
|
|
|
| 160 | 2 | Действия с рациональными числами
| Арифметические действия с рациональными числами. | Формулировать и записывать с помощью букв свойства действий с рациональными числами. | Действия с рациональными числами
|
|
|
| 161 | 3 | Действия с рациональными числами
| Преобразование числовых и буквенных выражений |
|
|
| 162 | 4 | Преобразование числовых и буквенных выражений | Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Подстановка выражений вместо переменных. | Читать и записывать буквенные выражения, составлять буквенное выражение по условию задачи. Вычислять числовое значение буквенного выражения при заданных значениях букв | Решение уравнений
|
|
|
| 163 | 5 | Решение уравнений
| Уравнение с одной переменной. Корень уравнения. Линейное уравнение. | Формулировать алгоритм решения уравнений алгебраическим способом. Решать простейшие уравнения алгебраическим способом, используя перенос слагаемых из одной части уравнения в другую.
| Решение уравнений
|
|
|
| 164 | 6 | Решение уравнений
|
|
|
| 165 | 7 | Решение задач
| Решение текстовых задач арифметическим способом.
| Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, моделировать условие с помощью схем, рисунков. | Действия с рациональными числами. Масштаб.
|
|
|
| 166 | 8 | Решение текстовых задач арифметическим способом. | Пропорции. |
|
|
| 167 | 9 | Итоговая контрольная работа за год |
|
|
|
|
| 168 | 10 | Анализ контрольной работы |
|
|
|
|
| Резерв (7 часов) |
| 169 | 1 | Отношения и пропорции
| Отношение, выражение отношения в процентах. Пропорции. Пропорциональная и обратно пропорциональная зависимости. | Решать текстовые задачи с помощью пропорции, основного свойства пропорции. | Отношение. Пропорция. Масштаб. Действия с рациональными числами
|
|
|
| 170 | 2 | Действия с рациональными числами
| Арифметические действия с рациональными числами. |
| Преобразование числовых и буквенных выражений |
|
|
| 171 | 3 | Преобразование числовых и буквенных выражений | Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Подстановка выражений вместо переменных. | Формулировать и записывать с помощью букв свойства действий с рациональными числами. | Решение уравнений
|
|
|
| 172 | 4 | Решение уравнений
| Уравнение с одной переменной. Корень уравнения. Линейное уравнение. | Пропорция. Масштаб. |
|
|
| 173 | 5 | Решение задач | Представление зависимости между величинами в виде формул. Решение текстовых задач арифметическим способом.
| Читать и записывать буквенные выражения, составлять буквенное выражение по условию задачи. Вычислять числовое значение буквенного выражения при заданных значениях букв | Пропорция, масштаб. Арифметические действия с обыкновенными и десятичными дробями. |
|
|
| 174 | 6 | Решение задач |
|
|
| 175 | 7 | Решение задач | Формулировать алгоритм решения уравнений алгебраическим способом. Решать простейшие уравнения алгебраическим способом, используя перенос слагаемых из одной части уравнения в другую.
|
|
|
| Анализировать и осмысливать текст задачи, переформулировать условие, извлекать необходимую информацию, моделировать условие с помощью схем, рисунков. |
|
|
|
|
|
1 Помимо указанных в данном разделе знаний, в требования к уровню подготовки включаются также знания, необходимые для освоения перечисленных ниже умений.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (6 кл.) (0.45 MB)
Рабочая программа по математике (6 кл.) (0.45 MB)
 0
0 955
955 62
62 Нравится
0
Нравится
0



