Решение квадратных уравнений различными способами
Работа ученицы 9В класса,
Ученицы ГБОУ № 76,
Ершовой Марии.
Цель:
Формирование понимания необходимости знания истории о квадратных уравнениях и различных способов решения квадратных уравнений
Задачи:
Обучающие:
- Сформировать представления о ценности исторических знаний о квадратных уравнениях.
- Познакомить с теорией и практикой применения десяти способов решения квадратных уравнений.
- Выработать умения выбирать рациональный способ решения квадратных уравнений и создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.
- Сформировать умения составлять алгоритмы для способов решения квадратных уравнений.
- Развитие вычислительных навыков.
- Развитие кругозора учащихся .
Развивающие:
- Формировать умения самостоятельно приобретать и применять знания, использовать различные источники информации и современные информационные технологии.
- Способствовать интеллектуальному развитию учащихся, формированию качеств мышления, познавательных интересов, творческих способностей учащихся.
- Из истории квадратных уравнений .
- Различные способы решения квадратных уравнений:
- Разложение левой части уравнения на множители. Метод выделения полного квадрата. Решение квадратных уравнений по формуле. Решение уравнений с использованием теоремы Виета. Решение уравнений способом переброски. Свойства коэффициентов квадратного уравнения. Графическое решение квадратного уравнения. Решение квадратных уравнений с помощью циркуля и линейки. Решение квадратных уравнений с помощью номограммы. Геометрический способ решения квадратных уравнений.
- Разложение левой части уравнения на множители.
- Метод выделения полного квадрата.
- Решение квадратных уравнений по формуле.
- Решение уравнений с использованием теоремы Виета.
- Решение уравнений способом переброски.
- Свойства коэффициентов квадратного уравнения.
- Графическое решение квадратного уравнения.
- Решение квадратных уравнений с помощью циркуля и линейки.
- Решение квадратных уравнений с помощью номограммы.
- Геометрический способ решения квадратных уравнений.
0 В уравнении коэффициенты, кроме а , могут быть отрицательными. Правило Брахмагупта по существу совпадает с нашим. Брахмагупта " width="640"
Квадратные уравнения в Индии.
- Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабахаттой. Другой индийский ученый, Брахмагупта ( VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ах 2 + b х = с, а 0
- В уравнении коэффициенты, кроме а , могут быть отрицательными. Правило Брахмагупта по существу совпадает с нашим.
Брахмагупта
Правило решения квадратных уравнений, изложенное в вавилонских текстах, совпадает по существу с современными, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решением, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Квадратным уравнением называется уравнение вида: ax 2 + bx + c = 0,
где х - переменная , а, b и с -некоторые числа, причем, а ≠ 0.
Если в квадратном уравнении ах 2 + bx + c = 0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением .
Решим уравнение:
х 2 + 10х – 24 = 0.
Разложим левую часть уравнения на множители:
х 2 + 12х – 2х – 24 =0
х (х + 12) – 2 (х +12) =0
(х + 12)(х – 2) = 0
х + 12 = 0 или х – 2 = 0 х 1 = -12
х 2 = 2
- Решим уравнение х 2 + 6х – 7 = 0
- Выделим в левой части полный квадрат. Для этого запишем выражение х 2 + 6х в следующем виде: х 2 + 6х = х 2 + 2· х · 3 .
- В полученном выражении первое слагаемое – квадрат числа х, а второе – удвоенное произведение х на 3, поэтому чтобы выделить полный квадрат, нужно прибавить 3 2 и вычесть 3 2, что бы уравнение осталось равносильным
х 2 + 6х – 7 =0 х 2 + 2· х ·3 + 3 2 – 3 2 – 7 = 0 (х + 3) 2 – 9 – 7 = 0 (х + 3) 2 – 16 = 0 (х + 3) 2 = 16 х + 3 = 4 или х +3 = - 4 , х 1 = 1 х 2 = – 7
0 – два корня, D =0 – один корень, он равен нулю, D 0 – нет корней. В данном уравнение D0 значит два корня. Вычислим: х = х = х 1 = х 2 = х 1 = х 2 = -1 " width="640"
Решим уравнение: 4х 2 + 7х + 3 = 0 а = 4, b = 7, с = 3 D = b 2 – 4 ас = 72 – 4· 4 ·3 = 49 – 48 = 1. Если D0 – два корня, D =0 – один корень, он равен нулю, D 0 – нет корней. В данном уравнение D0 значит два корня. Вычислим:
х =
х =
х 1 = х 2 = х 1 = х 2 = -1
0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p . Если p 0, то оба корня отрицательные, если p " width="640"
Квадратное уравнение имеет вид:
х 2 + px + q = 0.
Его корни удовлетворяют теореме Виета, которая при а = 1 имеет вид:
Следовательно (по коэффициентам p и q можно предсказать знаки корней).
а) Если свободный член q , приведенного уравнения положителен ( q 0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p .
Если p 0, то оба корня отрицательные, если p
0. ● Примеры 1. Решить уравнение х 2 – 9х + 14 =0 Попробуем найти два числа х 1 и х 2 , такие, что х 1 +х 2 = 9 х 1 х 2 = 14 Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения. " width="640"
б) Если свободный член q приведенного уравнения отрицателен ( q то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p 0.
● Примеры
1. Решить уравнение
х 2 – 9х + 14 =0
Попробуем найти два числа х 1 и х 2 , такие, что
х 1 +х 2 = 9
х 1 х 2 = 14
Такими числами являются 2 и 7. По теореме, обратной теореме Виета, они и служат корнями заданного квадратного уравнения.
Решим уравнение 2х 2 – 11х + 15 = 0.
Решение. «Перебросим» Рассмотрим квадратное уравнение:
ах 2 + b х + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение:
а 2 х 2 + а b х + ас = 0.
Пусть ах = у, откуда х = ; тогда приходим к уравнению
у 2 + by + ас = 0 .
у 2 – 11 y + 30 = 0.
Согласно теореме Виета:
Если в уравнении
x 2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
x 2 = – px – q .
Построим графики зависимостей у = х 2 и у = – px – q .
График первой зависимости – парабола, проходящая через начало координат.
График второй зависимости – прямая.
Возможны следующие случаи: прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
- прямая и парабола могут касаться (только одна общая точка),т.е. уравнение имеет одно решение;
- прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
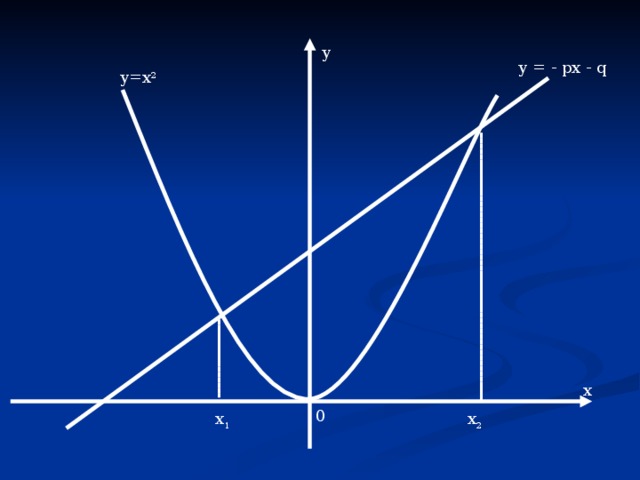
у
у = - рх - q
у=х 2
х
0
х 2
х 1
- Решим графически уравнение: х 2 – 3х – 4 = 0.
- Решим графически уравнение: х 2 – 3х – 4 = 0.
- Запишем уравнение в виде х 2 = 3х + 4 Построим параболу у = х 2 и прямую у = 3х + 4. Прямую у = 3х + 4 можно построить по двум точкам М (0;4) и N (3;13). Прямая и парабола пересекаются в двух точках А и B с абсциссами х 1 = – 1 и х 2 = 4.
- Запишем уравнение в виде х 2 = 3х + 4
- Построим параболу у = х 2 и прямую у = 3х + 4.
- Прямую у = 3х + 4 можно построить по двум точкам М (0;4) и N (3;13).
- Прямая и парабола пересекаются в двух точках А и B с абсциссами х 1 = – 1 и х 2 = 4.
у
у = - 3х + 4
у=х 2
х
4
- 1
Пусть дано квадратное уравнение: ах 2 + b х + с = 0, а ≠ 0.
I. Если а + b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то х 1 = 1, х 2 =
Доказательство . Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение:
х 2 + х + = 0.
Согласно теореме Виета:
По условию а + b + с = 0, откуда b = – а – с . Значит:
Получаем х 1 = 1, х 2 = , ч.т.д
II. Если а - b + с = 0, или b = а + с, то х 1 = – 1, х 2 = – .
- II. Если а - b + с = 0, или b = а + с, то х 1 = – 1, х 2 = – .
Доказательство . По теореме Виета:
По условию а – b + с = 0, откуда b = а + с. Таким образом:
т.е. х 1 = – 1 и х 2 = - , ч.т.д
Примеры
1. Решим уравнение 678х 2 – 137х – 541 = 0.
Решение. Так как а + b + с = 0 (678 – 137 – 541 = 0), то х 1 = 1, х 2 = = .
Ответ: 1; .
2. Решим уравнение 132х 2 + 247х + 115 = 0
Решение. Т. к. а- b +с = 0 (132 – 247 +115=0), то
х 1 = - 1, х 2 = -
Ответ: - 1; -
0, два различных корня; х = Ответ : 2; . " width="640"
III . Если второй коэффициент b = 2 k – четное число, то формулу корней:
х 1 , 2 =
можно записать в виде:
х 1 , 2 =
● Пример
Решим уравнение 3х 2 – 14х + 16 = 0.
Решение . Имеем: а = 3, b = – 14, c = 16, k = – 7;
D = k 2 – ac = (– 7) 2 – 3 · 16 = 49 – 48 = 1, D 0, два различных корня;
х =
Ответ : 2; .
Приведенное уравнение:
x 2 + px + q = 0
совпадает с уравнением общего вида, в котором а = 1, p и c = q . Поэтому для приведенного квадратного уравнения формула корней
х 1 , 2 =
принимает вид:
х 1 , 2 = или х 1 , 2 = - (3).
Формулу (3) особенно удобно использовать, когда p – четное число.
● Примеры
1. Решим уравнение х 2 – 14х – 15 = 0.
Решение . Имеем: х 1 , 2 = 7± = 7± = 7±8.
Ответ : х 1 = 15, х 2 = – 1 .
Следующий способ нахождения корней квадратного
уравнения: ах 2 + b х + с = 0
с помощью циркуля и линейки.
Допустим, что искомая окружность пересекает ось абсцисс в точках B (х 1 ;0) и D (х 2 ;0), где х 1 и х 2 – корни уравнения: ах 2 + b х + с = 0, и проходит через точки А (0;1) и С (0; ) на оси ординат. Тогда по теореме о секущих имеем ОВ∙О D = ОА ∙ ОС, откуда
ОС =
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд АС и BD, поэтому: SK= ;
SF= .
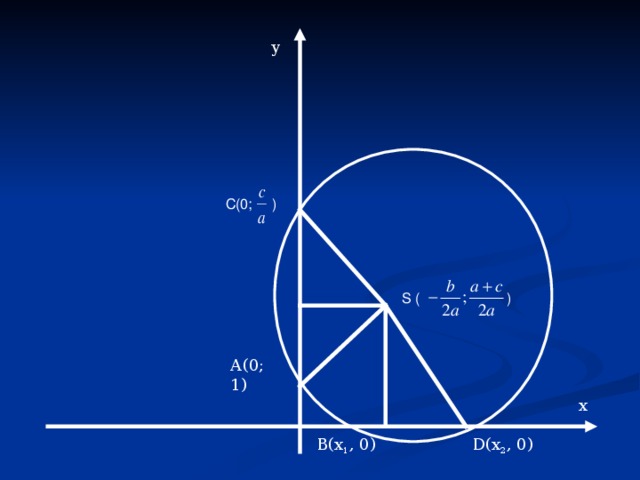
у
С(0; )
S ( )
А(0; 1)
х
В(х 1 , 0)
D (х 2 , 0)
- План решения уравнения: Построим точки S ( ; ) - центр окружности и А(0; 1);
- Проведем окружность с радиусом SA;
- Абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения. При этом возможны три случая:
- Радиус окружности больше ординаты центра
- Радиус окружности больше ординаты центра
- 2 корня.
b. Радиус окружности равен ординате центра
- 1 корень.
c. Радиус окружности меньше ординаты центра
- нет корней.
- - 2 корня. b. Радиус окружности равен ординате центра - 1 корень. c. Радиус окружности меньше ординаты центра - нет корней.
у
А (0;1).
х
– 9
1
0
S ( -4 ;- 4 )
Ответ : х 1 = – 9 , х 2 = 1 .
Это старый и незаслуженно забытый способ решения квадратных уравнений.
Номограмма для решения уравнения z 2 + pz + q = 0. Номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена по формулам:
ОВ = , АВ =
Полагая ОС = р, Е D = q , ОЕ = а ( все в см), из подобия треугольников САН и С DF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение z 2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
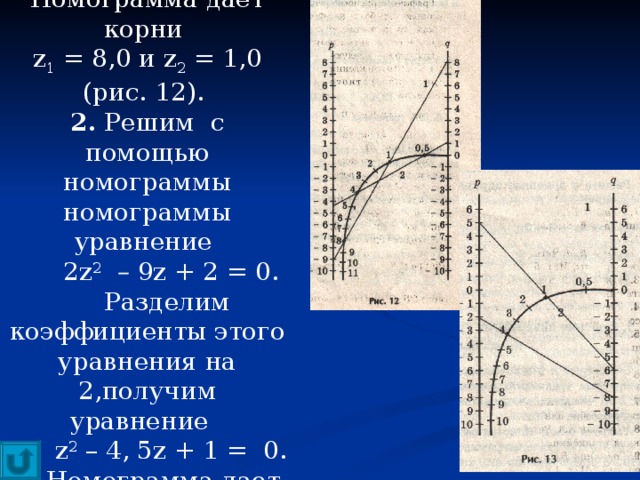
1. Для уравнения
z 2 – 9 z + 8 = 0.
Номограмма дает корни
z 1 = 8,0 и z 2 = 1,0 (рис. 12).
2. Решим с помощью номограммы
номограммы уравнение
2 z 2 – 9 z + 2 = 0.
Разделим коэффициенты этого
уравнения на 2,получим уравнение
z 2 – 4, 5 z + 1 = 0.
Номограмма дает корни z 1 = 4 и z 2 = 0,5.
Решим уравнение х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2 ,следовательно, площадь каждого равна 2 . Полученную фигуру дополняют затем до нового квадрата АВС D , достраивая в углах четыре равных квадрата, сторона каждого из них 2 , а площадь 6
6
2
6
x 2
2
2
6
6
2
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников
(4 ∙ 2,5х = 10х ) и четырех пристроенных квадратов(6,25 ∙ 4 = 25), т.е.
S = х 2 + 10х = 25. Заменяя х 2 + 10х числом 39, получим что S = 39+ 25 = 64, откуда следует, что сторона квадрата АВС D , т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
х 1 = 8 – 2,5 – 2,5 = 3; х 2 = -8-5=-13
Значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.
Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена вообще, просто ею не занимаются, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней.
Получите свидетельство
Вход
Способы решения квадратного уравнения (3.97 MB)
1
964
181
Нравится
0
