Урок по алгебре 8 класс.
Тема: «Сложение и вычитание дробей с разными знаменателями»
Цели:
Задачи:
Развивающие:
-
развивать логическое мышление;
-
развивать умение контролировать свои действия;
-
обучение действию по аналогии;
-
развивать культуру речи;
-
вырабатывать умение общения.
-
познавательную активность учащихся; навыки мыслительных операций сравнение, обобщение на протяжении урока;
Образовательные:
-
повторить теоретический материал по теме: «алгебраические дроби»;
-
описать способ сложения и вычитания алгебраических дробей с разными знаменателями;
-
отработать навыки сложения и вычитания алгебраических дробей с разными знаменателями;
-
расширять кругозор учащихся.
-
обеспечение усвоения образовательных стандартов.
-
развитие сотрудничества У-У.
-
осуществлять оперативный контроль процесса обучения.
Воспитательные:
-
вырабатывать умение преодолевать трудности ;
-
прививать интерес к предмету на основе связи с жизнью и практикой;
-
формировать умения высказывать свои мысли, слушать других, вести диалоги, отстаивать свою точку зрения;
-
формировать навыки самооценки;
-
добиться сознательного усвоения материала;
Коррекционные:
-
работать над повышением грамотности устной и письменной речи учащихся в ходе проговаривания алгоритма сложения и вычитания дробей с разными знаменателями и при выполнении письменной работы в тетради;
-
следить за осанкой учащихся при письме.
Методы: объяснительно-иллюстративный ( письменное упражнение на применение знаний с использованием таблиц и схем), репродуктивный (выполнение заданий по образцу с последующей проверкой)
Формы: фронтальная, индивидуальная, парная.
Оборудование: экран, мультимедийный проектор, карточки с заданиями, плакат «Сложение и вычитание дробей с разными знаменателями..
Тип урока: изучение нового материала.
Ход урока
Организационный момент (1 мин.)
– Здравствуйте ребята! Проконтролируйте свою готовность к уроку. На парте должны быть все принадлежности, тетрадь, учебник, дневник.( староста фиксирует в бланке готовность к уроку).
- Напоминаю ребята, что каждый урок, это трудный и познавательный процесс, от того как вы будете организовывать свою деятельность, будет зависеть ваша успеваемость и оценка за урок, которая будет складываться из всей вашей учебной деятельности на каждом этапе урока (на партах лежат каточки личной успеваемости)
Устная работа (5 мин.)
- Сегодня на уроке мы продолжим наше знакомство с алгебраическими дробями. Продолжим наш урок с повторения, используя ваши вопросы, которые вы подготовили к сегодняшнему уроку для ваших одноклассников на темы прошлых уроков ( один из учащихся задаёт вопрос, адресуя его на своё усмотрение другому, который на него отвечает, другие его выслушивают и оценивают, затем тот, кто отвечал, задаёт следующий вопрос другому и так далее; оцениваются как грамотно сформулированные вопросы , так и полные ответы).Слайд 5,6
– Какие действия мы уже умеем выполнять с алгебраическими дробями? (сокращение дробей, сложение и вычитание алгебраических дробей с одинаковыми знаменателями)
– Верно, но уметь складывать и вычитать дроби с одинаковыми знаменателями недостаточно. Как вы считаете, какие ещё действия нам необходимо научиться делать с алгебраическими дробями? (складывать и вычитать алгебраические дроби с разными знаменателями).
– Молодцы! Итак, мы продолжаем.
Приложение. Слайд 7
– Посмотрите, перед вами записаны несколько примеров.

– На какие три группы, вы разбили бы эти примеры ( учащиеся сравнивают и классифицируют примеры , дают полный ответ с пояснениями, выслушиваются ответы)
Слайд 8
| Сложение и вычитание рациональных дробей с одинаковыми знаменателями. | Сложение и вычитание обыкновенных дробей с разными знаменателями | Сложение и вычитание рациональных дробей с разными знаменателями. |
|
|
|
|
- Решите эти примеры 2 мин.
1(вариант) группа: №1, 5, 4
2 ( вариант) группа: № 2, 3, 6.
- Все ли примеры удалось решить? ( решили № 1,2, 5,3). Проверяются у доски, 4 учащихся записываются решения примеров № 1,2, 5,3.
-Какие примеры вызвали затруднения, как вы думаете, почему (№ 4, 6 – не знаем алгоритма решения).
- Я думаю, главная проблема на сегодняшний урок определена.
- Сформулируйте тему сегодняшнего урока («Сложение и вычитание алгебраических дробей с разными знаменателями») и запишите ёё в тетрадь.
– Какую же цель мы поставим перед собой на урок? (научиться складывать и вычитать алгебраические дроби с разными знаменателями).
– Что нам необходимо вывести для достижения нашей цели? (алгоритм приведения алгебраических дробей к общему знаменателю, чтобы потом по известному правилу, складывать и вычитать дроби уже с одинаковым знаменателем).
3. Объяснение нового материала (15 мин.)
– Чтобы вам было легче вывести алгоритм, давайте устно вспомним алгоритм решения примеров «Сложение и вычитание обыкновенных дробей с разными знаменателями».
- Каким алгоритмом вы пользовались, решая 2 группу примеров? Заслушиваются 2- 3 алгоритма учащихся.
- Слайд 9.
-Давайте ещё раз посмотрим алгоритм слайд 7 сложение и вычитание обыкновенных дробей с разными знаменателями. Проанализируйте, сравните эти решения, сделайте выводы.
- Как вы думаете, можно воспользоваться этим алгоритмом при решении примеров № 4, 6?
- .Давайте составим алгоритм сложения и вычитания рациональных дробей с разными знаменателями. Работа в парах.(2 мин). Заслушиваться 2 – 3 алгоритма, затем объединяются в алгоритм в таблице.
Слайд 10
| Сложение и вычитание обыкновенных дробей с разными знаменателями | Сложение и вычитание рациональных дробей с разными знаменателями. | |
24 = 2 НОК (22; 36)= 2 Находим дополнительные множители:
Ответ:
| 1)Надо привести дроби к общему знаменателю. 2)Дроби несократимые и их знаменатели взаимно простые числа. Надо привести дроби к общему знаменателю. | |
| Пример:
15: 5 = 3 .
4) |
( раскрыть скобки, привести подобные слагаемые)
| |
- Один из учащихся демонстрирует решение примера № 6 с полным объяснением алгоритма решения, остальные внимательно выслушивают, если это необходимо дополняют ответ. Оценивают ответ учащегося у доски.
Работа с учебником (5 мин).
– А теперь, вам необходимо разобрать примеры №1,2.3 из учебника, работа в парах. Вам необходимо провести исследовательскую работу и выяснить: на какие основные вопросы вы должны знать ответы, чтобы успешно решать примеры на сложение и вычитание алгебраических дробей с разными знаменателями? Сделайте выводы. ( Учащиеся предлагают свои вопросы. Как найти общий знаменатель? Как разложить на множители знаменатели дробей? Как найти дополнительные множители? Как привести дроби к общему знаменателю? Как представить сумму и разность дробей в виде несократимой рациональной дроби?)
- Продолжите работу в пара. Поставьте вопросы друг за другом таким образом, чтобы получился алгоритм для решения примеров ( учащиеся работают в парах и предлагают свои ответы, ответы анализируются и сравниваются, объединяются в общее решение)
Слайд 11
Алгоритм.
-
Как найти общий знаменатель дробей?
- Разложить знаменатели дробей на простейшие множители .
- Выписать все множители одного из разложений и дополнить разложениями другого ( или выписать одинаковые множители из разложений и дополнить не выделенными множителями).
- Перемножить выписанные множители.
-
Как привести дроби к общему знаменателю?
- Найти дополнительные множители, разделив общий знаменатель на знаменатель каждой дроби.
- Перемножить числители дробей с дополнительными множителями
- Записать дроби под общий знаменатель.
-
Как представить сумму дробей в виде несократимой рациональной дроби?
- при необходимости раскрыть скобки, привести подобные слагаемые, сократить дробь.
Слайд 12, 13, 14,15,16,17
Давайте ещё раз рассмотрим решение примеров №1 , 2, 3 с помощью проектора.
Трое учащихся по желанию могут описать ход решения примеров, проговаривая все этапы алгоритма, дать более полное объяснение. Остальные учащиеся оцениваю полноту ответа , дополнять , задавать вопросы, если объяснение было непонятным.
Пример 1

Решение.
-
Приведём дроби к общему знаменателю:
- Разложим на множители знаменатели дробей.
4 а b = 2 2 а а а b;
b = 2 2 а а а b;
6а b = 2 3 a b b b b;
= 2 3 a b b b b;
- Найдём общий знаменатель :
ОЗ: 2 а b 2 3 b b b a a = 12 a b
b ;
;
-
Найти дополнительные множители:
-

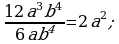
-
Перемножим числители дробей с дополнительными множителями :

4)Представим сумму дробей в виде несократимой рациональной дроби.

Пример 2

Решение.
-
Приведём дроби к общему знаменателю:
- Разложим знаменатели дробей на простые множители
 + аb = a (a + b ) ;
+ аb = a (a + b ) ;
ab +  = b ( a+ b) ;
= b ( a+ b) ;
- Найдём общий знаменатель:
ОЗ : ( a+ b) а b .
- Найдём дополнительные множители:
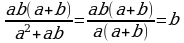 ;
;
 ;
;
-
Перемножим дополнительные множители с числителями дробей:
 ;
;
-
Приведём дробь к виду несократимой дроби (приведём подобные слагаемые, в числителе вынесем общий множитель и разложим числитель на множители, сократим получившуюся дробь)

Пример 3.
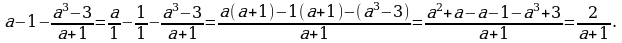
Решение.
-
Представим первое и второе слагаемые в виде дроби.

-
Найдём общий знаменатель : (a+1).
Найдём дополнительные множители.

-
Перемножим дополнительные множители с числителями дробей:
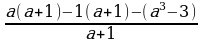 .
.
-
Представим дробь в виде несократимой дроби.
Приведём подобные слагаемые: 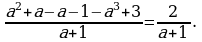
– Прекрасно поработали!
-
Первичное закрепление (10 мин.)
Ребята, мы с вами отлично поработали над алгоритмом, но как вы понимаете необходимо научиться его применять при решении примеров.
№73 (а, б, в, г, д ) устно.( отвечают 4 учащихся)
Ученик устно проговаривает план решения, учащиеся могут его корректировать, при необходимости корректирует учитель, если допущены ошибки. Учащиеся оценивают ответы .
№ 73 (е) Ученик работает у доски, комментируя все этапы решения. .
№ 74 (а, б, г, е) выполняют у доски три ученика, остальные в тетрадях. Решения проверяем, если возникло затруднение, учащиеся помогают и дополняют с места. Правильно выполненные примеры оцениваются.
№ 75 (а) Ученик работает у доски, в это время остальные выполняют № 75 (б) – решение проверяется. Учащийся комментирует своё решение. Учащийся оценивает свой ответ . Учащиеся проверяют ход решения отвечающего у доски и оценивают его ответ .
Слайд 18 ( № 75)
№ 75 ( а)

№ 75 ( б)


5. Самостоятельная работа (5 мин.)
Слайд 19
Самостоятельная работа по вариантам 1 вариант -№76(а,в,д), 2 вариант -№ 76 ( б,г,е)
Слайд 20
№ 76 (а, в,д)

Слайд 21
№ 76 (б, г, д)
 )
)
После выполнения работы проводится проверка (слайд 10). Проверяя решение, учащиеся отмечают «+» – правильное решение и «?» – неверное решение. Ученики, допустившие ошибку, должны объяснить причину, по которой они не справились с заданием.
6. Включение новых знаний в систему (7 мин.)
–Для выполнения следующих заданий вам потребуются не только знание алгоритма, но умение применять его в более сложных ситуациях. Учащимся предлагаются примеры № 86(в), № 93(б), работа в парах. После выполнения проверяем ответы
Слайд 22 *самостоятельная работа
Слайд 23 № 86 (в)

Слайд 24 № 93 (б)

7. Итог урока, рефлексия (2 мин.) Слайд 25
– Какую цель вы поставили сегодня на уроке? (Научиться складывать и вычитать дроби с разными знаменателями).
– Что вам позволило достигнуть эту цель? (Алгоритм нахождения общего знаменателя для алгебраических дробей, вывели правило сложения и вычитания дробей с разными знаменателями).
– Какие этапы алгоритма вы сегодня использовали ? Какие правила вы сегодня вспомнили из курса 5-7 классов. (Находили наименьший общий знаменатель дробей, дополнительные множители, формулы сокращенного умножения, правила раскрытия скобок).
Рефлексия. Слайд 26
– Перед вами лежит карточка. Поставьте «+» рядом с тем высказыванием, которое для вас является истинным.
-
Данная тема мне понятна.
-
Я знаю, как найти общий знаменатель для дробей.
-
Я умею находить дополнительные множители.
-
В самостоятельной работе у меня все получилось.
-
Я понял (а) причину своих ошибок в самостоятельной работе.
-
Мне было легко решать примеры в паре.
-
Я доволен своей работой на уроке.
Карточки ребята сдают учителю.
8. Домашнее задание (1 мин.)
Выучит алгоритм нахождения наименьшего общего знаменателя алгебраических дробей и правило сложения и вычитания дробей с разными знаменателями. Составить карточки памятки алгоритмом решения примеров из п. 4 № 1, 2, 3 №77 , 78( а,в), 93(в). Составить один пример на сложение и вычитание дробей с разными знаменателями и решить его.

 Получите свидетельство
Получите свидетельство Вход
Вход






 2
2














 "Сложение и вычитание дробей с разными знаменателями" (110.67 KB)
"Сложение и вычитание дробей с разными знаменателями" (110.67 KB)
 0
0 428
428 6
6 Нравится
0
Нравится
0



