Автор: Плотникова Е.В., учитель математики МБОУ СОШ № 7 г.Бирска
Тип урока: ОНЗ
Тема: «Сложение и вычитание дробей с разными знаменателями»
Основные цели:
1) составить алгоритм сложения и вычитания дробей с разными знаменателями,
2) тренировать умение использовать составленный алгоритм;
Демонстрационный материал:
задания для актуализации знаний + пробное задание: игра «Паровозик»;
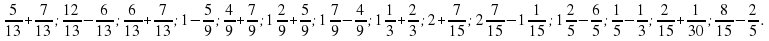
эталоны правила сложения и вычитания дробей с разными знаменателями:
найти НОК знаменателей;
для каждой дроби найти дополнительный множитель;
записать пример с новыми дробями;
сложить (вычесть) дроби по известному правилу, если возможно – сократить.
3) презентация.
Раздаточный материал:
эталоны нового знания («Построй свою математику», блок – тетрадь эталонов);
карточки для рефлексии
1) Сегодня на уроке мы учились ______________________________.
2) Для успешного выполнения сложения (вычитания) дробей с разными знаменателями надо уметь ____________________ .
3) На уроке я ________________________________.
4) У меня остались затруднения_________________.
Ход урока
1. Мотивация к учебной деятельности (Слайд 1)
Цель:
1) включение учащихся в учебную деятельность;
2) организовать деятельность учащихся по установке тематических рамок: сложение и вычитание дробей с одинаковыми знаменателями;
3) создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность.
Организация учебного процесса на этапе 1:
– С какими числами вы уже знакомы? (Натуральные числа, дроби, смешанные числа.)
– Какие арифметические действия вы умеете делать с натуральными числами? (Складывать, вычитать, умножать, делить, возводить в степень, сравнивать).
– Какие арифметические действия вы умеете делать с дробями? (Складывать, вычитать, сравнивать).
– Какие из этих арифметических действий с дробями изучались вами в пятом классе? (Сравнение дробей).
– А узнали ли вы что-то новое о сравнении дробей? (Да. Мы узнали как сравнивать дроби с разными знаменателями, узнали новые способы сравнения дробей).
2. Актуализация знаний и фиксация затруднения в пробном учебном действии.
Цель:
1) организовать актуализацию изученных способов сложения и вычитания дробей с одинаковыми знаменателями, достаточных для построения нового знания: сложение и вычитание дробей с разными знаменателями;
2) зафиксировать актуализированные способы действий в речи;
3) организовать обобщение актуализированных способов действий;
4) организовать актуализацию мыслительных операций, достаточных для построения нового знания: анализ, сравнение, обобщение;
5) мотивировать к выполнению пробного действия;
6) организовать самостоятельное выполнение пробного учебного действия;
7) организовать фиксацию индивидуальных затруднений в выполнении учащимися пробного учебного действия или в его обосновании.
Организация учебного процесса на этапе 2:
Вы раньше работали с обыкновенными дробями? Что вы умеете с ними делать? (Переводить неправильную дробь в смешанное число и наоборот, сравнивать дроби, приводить дроби к наименьшему общему знаменателю, складывать дроби, вычитать.)
- Вспомните правила сложения и вычитания дробей. (Слайд 2)
Посмотрите на доску и скажите, какие задания вам будут предложены в начале урока? (Задания на повторение знаний необходимых для изучения нового материала).
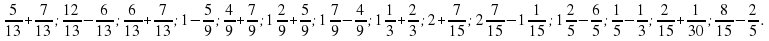
На доске игра «Паровозик» (Повторить сложение и вычитание дробей с одинаковыми знаменателями)
3. Выявление места и причины затруднения
Цель:
1) организовать восстановление выполненных операций;
2) организовать фиксацию места (шага, операции), где возникло затруднение;
3) организовать соотнесение своих действий с используемыми эталонами (алгоритмом, понятием и т.д.);
4) на этой основе организовать выявление и фиксацию во внешней речи причины затруднения – тех конкретных знаний, умений или способностей, которых недостает для решения исходной задачи и задач такого класса или типа вообще.
Организация учебного процесса на этапе 3:
– Какое задание вы должны были выполнить? (Сложить и вычесть дроби.)
Что нового в задании? (Разные знаменатели)
В чём у вас затруднение? (Мы не смогли найти сумму (разность) дробей с разными знаменателями.)
А почему у вас возникло затруднение? Вы же утверждали, что умеете складывать и вычитать дроби! (Известное нам правило не годится.) (Слайд 4)
– Обоснуйте свое высказывание? (У нас нет алгоритма сложения и вычитания дробей с разными знаменателями.)
Сформулируйте цель. (Составить алгоритм сложения (вычитания) дробей с разными знаменателями).
Сформулируйте тему урока. (Сложение и вычитание дробей с разными знаменателями.) (Слайд 5)
- Откройте тетради, запишите число и тему урока.
А может кто-то из вас уже догадался, как справиться с затруднением?
4. Построение проекта выхода из затруднения
Цель:
организовать построение проекта выхода из затруднения:
учащиеся ставят цель проекта (целью всегда является устранение причины возникшего затруднения);
учащиеся уточняют и согласовывают тему урока;
учащиеся определяют средства (алгоритмы, модели, справочники и т.д.);
учащиеся формулируют шаги, которые необходимо сделать для реализации поставленной цели.
Организация учебного процесса на этапе 4:
– Какую цель вы поставите перед собой? (Изменить алгоритм сложения и вычитания дробей с одинаковыми знаменателями, научиться пользоваться уточнённым алгоритмом.)
Какой план для работы вы можете предложить? (Соединить алгоритмы сложения (вычитания) дробей с одинаковыми знаменателями и сложения (вычитания) дробей с разными знаменателями, сформулировать новый алгоритм для дробей с разными знаменателями, применить уточнённый алгоритм для решения пробного задания.) (Слайд 6)
5. Реализация построенного проекта
Цель:
1) организовать реализацию построенного проекта в соответствии с планом;
2) организовать фиксацию нового способа действия в речи;
3) организовать фиксацию нового способа действия в знаках (с помощью эталона);
4) организовать фиксацию преодоления затруднения;
5) организовать уточнение общего характера нового знания (возможность применения нового способа действий для решения всех заданий данного типа).
Организация учебного процесса на этапе 5:
Ребята предлагают свои варианты уточнения алгоритма, проходит обсуждение, обязательно обратить внимание на свойства, которые используются при построении алгоритма.
В результате обсуждений на экране вывешивается уточнённый алгоритм. (Слайд 7)
Ребята получают эталоны и записывают в них правильное решение примеров.
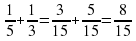 ; (Слайд 8 – темный экран)
; (Слайд 8 – темный экран)
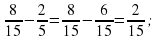
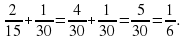
Какие задания вы теперь сможете выполнять? (На сложение и вычитание дробей с разными знаменателями)
Что теперь необходимо сделать? (Закрепить умение применять этот алгоритм к решению примеров)
6. Первичное закрепление во внешней речи
Цель:
организовать усвоение детьми нового способа действий при решении данного класса задач с их проговариванием во внешней речи: фронтально.
Организация учебного процесса на этапе 6:
№ 197 (е, л)
Задание выполняется у доски с проговариванием шагов построенного алгоритма.
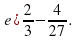
1) Привести дроби к общему знаменателю, для этого найдем НОК(3 и 27): НОК(3 и 27) = 27
2) Найдем дополнительные множители к каждой дроби: для первой дроби дополнительный множитель равен 27:3=9, а для второй дроби – 27:27=1
3) Запишем дроби со знаменателем 27: 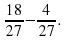
4) Выполнить вычитание по известному правилу: 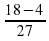
5) Записать ответ и убедиться, что в ответе несократимая дробь: 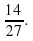
Запись на доске: 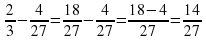
НОК(3 и 27) = 27.
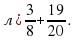
1) Привести дроби к общему знаменателю, для этого найдем НОК(8 и 20): НОК(8 и 20) = 40.
2) Найдем дополнительные множители к каждой дроби: для первой дроби дополнительный множитель равен 40:8=5, а для второй дроби – 40:20=2.
3) Запишем дроби со знаменателем 40: 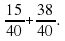
4) Выполнить вычитание по известному правилу: 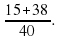
5) Записать ответ и убедиться, что в ответе несократимая дробь: 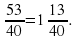
Запись на доске: 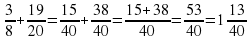
НОК(8 и 20) = 40.
7. Самостоятельная работа с самопроверкой по эталону
Цель:
1) организовать самостоятельное выполнение учащимися типовых заданий на новый способ действия;
2) организовать соотнесение работы с эталоном для самопроверки (в случае, когда учащиеся начинают осваивать процедуру грамотного самоконтроля возможно соотнесение работы с подробным образцом);
3) организовать вербальное сопоставление работы с эталоном для самопроверки*
(в случае, когда способ действия состоит из нескольких шагов – организация пошаговой проверки);
4) по результатам выполнения самостоятельной работы организовать рефлексию деятельности по применению нового способа действия.
* В случае, когда учащиеся начинают осваивать процедуру грамотного самоконтроля возможно вербальное сопоставление работы с подробным образцом.
Организация учебного процесса на этапе 7:
Что теперь необходимо сделать?
Для самостоятельной работы я предлагаю выполнить №№ 197 (ж, о). (задания выполняются в парах, с проверкой по образцу ) (Слайды 9 и 10) 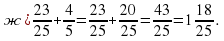
НОК(25 и 5) = 25.
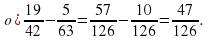
НОК(42 и 63) = 126.
У кого возникло затруднение при нахождении суммы?
В каком месте возникло затруднение?
Почему у вас возникло затруднение при нахождении суммы?
У кого возникло затруднение при нахождении разности?
В каком месте возникло затруднение?
Почему у вас возникло затруднение при нахождении разности?
Кто решил задание правильно?
8. Рефлексия деятельности на уроке
Цель:
1) организовать фиксацию нового содержания, изученного на уроке;
2) организовать рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся;
3) организовать оценивание учащимися собственной деятельности на уроке;
4) организовать фиксацию неразрешённых затруднений на уроке как направлений будущей учебной деятельности;
5) организовать обсуждение и запись домашнего задания.
Организация учебного процесса на этапе 8:
– Сегодня на уроке вы учились….?
Для успешного выполнения сложения (вычитания) дробей с разными знаменателями надо уметь …
– На уроке я…
– У меня остались затруднения…
– В чём были затруднения?
Домашнее задание:
| п.3.2.1.; учить алгоритмы в эталонах, №№ 197 (в,г,и,к), 217. |


 Получите свидетельство
Получите свидетельство Вход
Вход



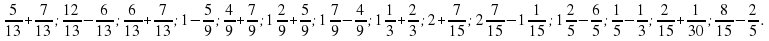
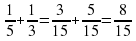 ; (Слайд 8 – темный экран)
; (Слайд 8 – темный экран) 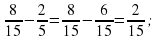
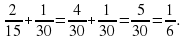
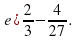
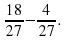
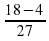
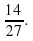
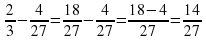
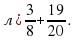
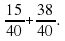
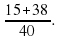
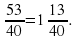
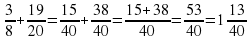
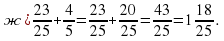
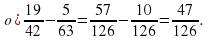









 Разработка урока по математике «Сложение и вычитание дробей с разными знаменателями» (29.03 КB)
Разработка урока по математике «Сложение и вычитание дробей с разными знаменателями» (29.03 КB)
 0
0 1331
1331 129
129 Нравится
0
Нравится
0


