За время преподавания математики в среднем и старшем звене пришло понимание составления алгоритмов для работы по некоторым темам, отраженных в данных схемах-опорах.
Готовые алгоритмы упрощают запоминание материала, готовая картинка воспринимается лучше, чем готовое правило.
Некоторые из них составлялись на уроках вместе с детьми.
Например, схема-опора «Найти область определения функции» вводится в восьмом классе при изучении темы функции вида: «» и заканчивается в одиннадцатом классе при изучении логарифмической функции. Восьмиклассники видят перспективу, выпускники – весь программный материал.
Схемы-опоры позволяют возвращаться к пройденному материалу, более рационально готовить учащихся к ЕНТ. При повторении на каком-либо этапе использование схем-опор экономит время на уроке.
Схемы-опоры оформляются в рабочей ученической тетради на ее форзаце от руки самим учеником. Схемы-опоры имеются у учителя красочно оформленные.

1) Рациональный устный счет:
(переход через десяток)
2) Длина отрезка на координатной прямой:
Длина=Б-М
Б-большее, М-меньшее
Длина=П-Л
П-правая, Л-левая
3) Сложение чисел с разными знаками:
ПОЛ+ОТР=ОТНИМАЕМ
(ПОЛ, ОТР) какое больше
ОТР+ОТР=СКЛАДЫВАЕМ
(ОТР)
4) Сложение и вычитание обыкновенных дробей с разными знаменателями:
Вопрос: ДЕЛИТСЯ ЛИ?
Ответ:
1) ДА, делится.
2) НЕТ, не делится.
3) НЕТ, не делится, НО…
5) Сложение и вычитание рациональных дробей с разными знаменателями:
ЧИСЛА,
БУКВЫ,
СКОБКИ
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


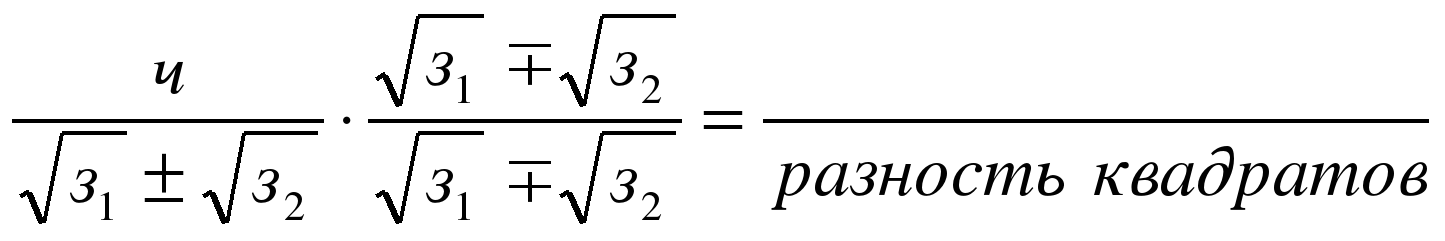









 Схемы-опоры по математике (0.12 MB)
Схемы-опоры по математике (0.12 MB)
 0
0 1725
1725 140
140 Нравится
0
Нравится
0







