"Системы счисления"

Системы счисления

Способы записи чисел

СОДЕРЖАНИЕ

1. Понятие и сущность систем счисления

2. Сравнительный анализ древних систем счисления

3. Десятичная система счисления

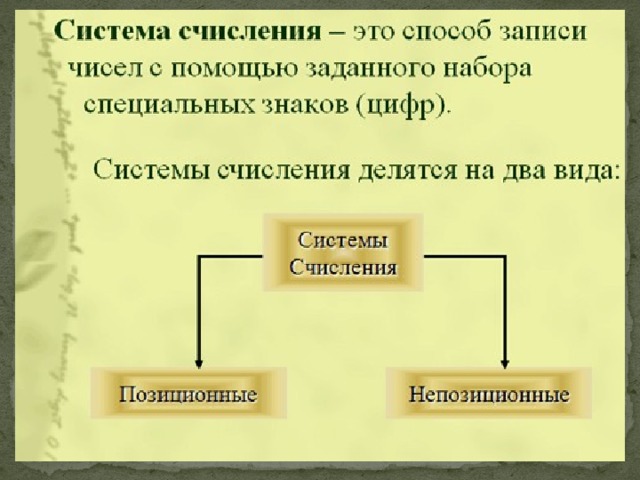
позиционные

непозиционные

Количественные значения символов, используемых для записи чисел, не зависит от их положения (места) в коде числа

Количественные значения символов, используемых для записи чисел, зависит от их положения (места) в коде числа

• В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе. Так, например, в римской системе счисления в числе XXXII (тридцать два) вес цифры X в любой позиции равен просто десяти.

• В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любая позиционная система характеризуется своим основанием.

Мы привыкли считать и записывать числа

в десятичной системе счисления.

Но образование данной системы длилось веками, уходя своими корнями за нашу эру.

Система, изобретенная первобытным человеком, была достаточно примитивной, т.к. в ней не содержалось никаких правил для оперирования с числами. Такой вид счета носит название унарной системы счисления , т.е. системы счисления, в которой для записи числа применяется только один вид знаков

Следы такого рода счета сохранились у многих народов и до настоящего времени. Иногда эти примитивные орудия счета (камешки, раковинки, косточки) нанизывались на шнурок или палочку, чтобы их не растерять; данный обычай впоследствии послужил к созданию более совершенных счетных приборов, сохранивших свое значение и до наших дней.

Неудобства такой системы записи чисел и ограниченность ее применения оче­видны: чем большее число надо записать, тем длиннее строка из палочек; при записи большого числа легко ошибиться - нанести лишнее количество палочек или, наоборот, не дописать палочки.

Оригинальность унарной системы заключается в том, что по типу ее можно отнести как к позиционной, так и к непозиционной системе.

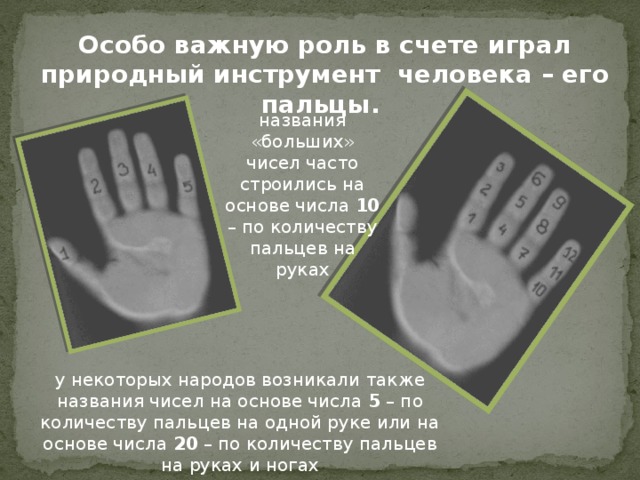
Особо важную роль в счете играл природный инструмент человека – его пальцы.

названия «больших» чисел часто строились на основе числа 10 – по количеству пальцев на руках

у некоторых народов возникали также названия чисел на основе числа 5 – по количеству пальцев на одной руке или на основе числа 20 – по количеству пальцев на руках и ногах

ДРЕВНИЕ СИСТЕМЫ СЧИСЛЕНИЯ

Алфавитные системы

счисления

Система счисления

в Древнем Египте

Иероглифическая система счисления имеет основание 10 и не является позиционной: для обозначения чисел 1, 10, 100 и т.д. в ней используются разные символы, каждый символ повторяется определенное число раз, и, чтобы прочитать число, нужно просуммировать значения всех символов, входящих в его запись. Таким образом, их порядок не играет роли, и они записываются либо горизонтально, либо вертикально.

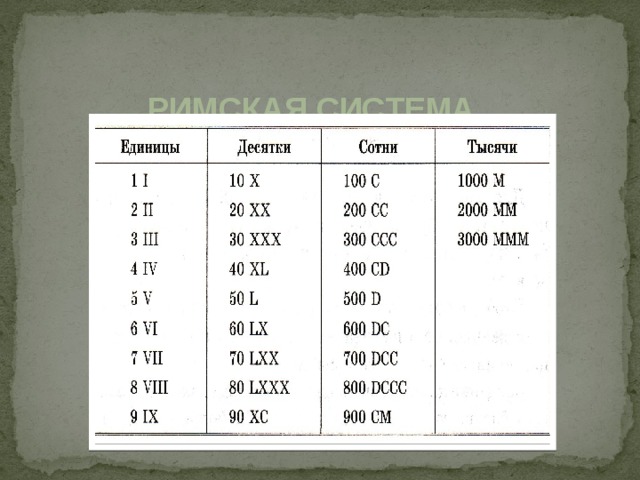
Римская система

счисления

• До нас дошла римская система записи чисел, которая в некоторых случаях применяется в нумерации (века, тома в собрании сочинений и др.). В римской системе в качестве цифр используются латинские буквы:
• I V X L C D M
• 1 5 10 50 100 500 1000
• Эта система непозиционная. В ней цифры записываются слева направо. Если слева записана меньшая цифра, а справа - большая, то их значения вычитаются. Наоборот - складываются.

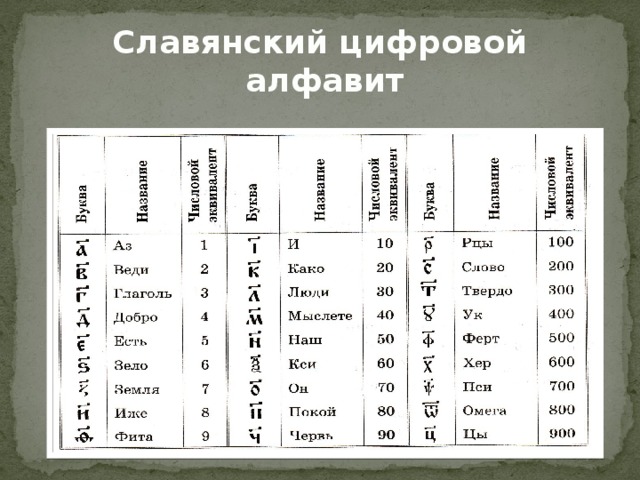
Славянский цифровой

алфавит

Славянская глаголическая нумерация

Наш современный алфавит также имеет цифровые значения

Система счисления ацтеков и майя

У ацтеков и майя, населявших американский континент и создавших там высокую культуру, почти полностью уничтоженную

испанскими завоевателями в XVI - XVII в., была принята

двадцатеричная система счисления.

Та же система была принята у кельтов, населявших Западную Европу, начиная со II тысячелетия до нашей эры.

Вавилонская система

счисления

• является комбинацией шестидесятеричной и десятичной систем с применением позиционного принципа;
• используется всего два символа для обозначения числа 1 и числа10 .
• шестидесятеричной системой пользуются до сих пор при измерении времени и углов.

Ясачные грамоты

Многочисленные следы различных систем сохранились до нашего времени, однако, для выполнения вычислений мы всегда пользуемся десятичной системой.

К VII—V вв. до н. э. относятся первые индийские письменные математические памятники . Мы называем изобретенные индийцами цифры 1, 2, .., 9 и нуль арабскими, так как заимствовали их у арабов, но сами арабы называли эти цифры индийскими, а арифметику, основанную на десятичной системе — “индийским счетом”

  Эволюция арабских цифр

Время многократно изменяло облик десятичных цифр , пока они не приобрели привычный для нас вид . Некогда написание цифр было таким:

Такое изображение десятичных цифр не случайно : каждая цифра обозначает число , соответствующее количеству углов в ней . Подсчитайте и убедитесь в этом сами!

Структура десятичной системы счисления.

Основание этой системы счисления p равно десяти. В этой системе счисления используется десять цифр. В настоящее время для обозначения этих цифр используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число в десятичной системе счисления записывается как сумма единиц, десятков, сотен, тысяч и так далее.

Десятичная система счисления, наиболее распространённая система счисления. Основанием Д. с. с. является число 10, которое образует единицу 2-го разряда, единицей 3-го разряда будет 100 = 102, вообще единица каждого следующего разряда в 10 раз больше единицы предыдущего Д. с. с. основана на позиционном принципе, т. е. в ней один и тот же знак (цифра) имеет различные значения в зависимости от того места, где он расположен. В связи с этим для записи всех чисел нуждаются в особых символах только первые 10 чисел. Символы эти, обозначаемые знаками 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называются цифрами.

Арифметические действия над десятичными числами производятся с помощью достаточно простых операций , в основе которых лежат известные каждому школьнику таблицы умножения и сложения , а также правило переноса : если в результате сложения двух цифр получается число , которое больше или равно 10 , то оно записывается с помощью нескольких цифр , находящихся на соседних позициях . Изучаемые в самом раннем возрасте , эти правила в результате повседневной практики усваиваются так прочно , что мы оперируем ими уже подсознательно . По этой причине сегодня многие люди даже и не догадываются о существовании других систем счисления.

Для углубления своих знаний по этой теме

используйте литературу:

• Энциклопедический словарь юного математика.- М.: «Педагогика»

И.Г. Семакин, Е. Г. Хеннер «Информатика 7-9 класс» -

М.: Лаборатория базовых знаний,2000

• О.Ефимова, В.Морозова, Н.Угринович «Курс компьютерной технологии» учебное пособие для старших классов.-М.: ООО «Издательство АСТ»2000

• М.Клайн «Математика. Поиск истины.»- М.: «Мир»1988

• Учебники по информатике Кушниренко,Гейна, Есипова и других авторов.

• А. Даан - Дальмедико, Ж. Пейффер «Пути и лабиринты. Очерки по истории математики» :Пер. с франц.-М.: Мир,1986