Конспект урока по информатике 8 класс
Тема урока: «Системы счисления»
Цель: обеспечить усвоение знаний о системах счисления; формировать умение определять основание и алфавит систем счисления.
Задачи:
Научится преобразовывать основание и алфавит систем счисления, переходить от свернутой формы записи числа к его развернутой записи. Познакомиться с разнообразием систем счисления.
Ход урока
Организационный момент. (Учитель приветствует учеников, проверяет наличие учебника, тетради и др.).
Сегодня на уроке мы пройдем такую тему как «Общие сведения о системах счисления».
Кто-нибудь может предположить, что такое «Система счисления»?
Итак, Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа, называются цифрами, а их совокупность — алфавитом системы счисления.
Данные знания будут вам необходим, особенно тем, кто собирается связать свою жизнь с информатикой.
Система счисления – это принятый способ записи чисел и сопоставления этим записям реальных значений. Все системы счисления можно разделить на два класса:
позиционные – количественное значение каждой цифры зависит от ее место положения (позиции) в числе;
непозиционные – цифры не меняют своего количественного значения при изменении их положения в числе.
Для записи чисел в различных системах счисления используется определенное количество знаков или цифр. Число таких знаков в позиционной системе счисления называется основанием системы счисления.
| Основание | Название системы счисления | Знаки |
| 2 | Двоичная | 0, 1 |
| 3 | Троичная | 0, 1, 2 |
| 4 | Четверичная | 0, 1, 2, 3 |
| 5 | Пятиричная | 0, 1, 2, 3, 4 |
| 8 | Восьмиричная | 0, 1, 2, 3, 4, 5, 6, 7 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| 12 | Двенадцатиричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В |
| 16 | Шестнадцатиричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, C, D, E, F |
Каждое число в позиционной системе счисления можно представить в виде суммы произведений коэффициентов на степени основания системы счисления. Например:
![]() (степени расставляем над целой частью числа слева направо, начиная с «0»)
(степени расставляем над целой частью числа слева направо, начиная с «0»)
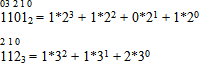
Теперь рассмотрим алгоритм перевода чисел из произвольной системы счисления в десятичную на примере.
Алгоритм перевода чисел из произвольной системы счисления в десятичную:
![]()
(степени расставляем над целой частью числа слева направо, над дробной частью – справа налево, начиная с «-1»)
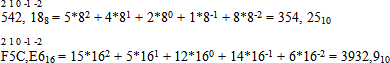
Двоичная система счисления имеет особую значимость в информатике. Это определяется тем, что внутреннее представление любой информации в компьютере является двоичным, т. е. описываемым наборами только из двух знаков (0, 1).
Рассмотрим пример перевода числа из десятичной системы счисления в двоичную:

Пояснение: Решение оформляется на доске учителем с четким объяснение каждого своего действия.
Результатом является число, составленное из остатков от деления на 2 (которые мы обводили в кружок), записанное справа налево.
34210 = 1010101102
Теперь попробуйте записать рассмотренный алгоритм перевода числа из десятичной системы счисления словами(на выполнения задания отводится 2-3 мин., учитель контролирует его выполнение). По истечении отведенного времени учитель просит нескольких учеников прочитать составленный ими алгоритм. Затем остальные учащиеся под руководством учителя корректируют алгоритм. Учитель формулирует алгоритм, учащиеся записывают его в рабочие тетради.
Алгоритм перевода десятичных чисел в двоичную систему счисления:
Разделить число на 2. Зафиксировать остаток (0 или 1) и частное.
Если частное не равно 0, то разделить его на 2, и так далее пока частное не станет равно 0. Если частное равно 0 , то записать все полученные остатки, начиная с первого, справа налево.
Теперь мы знаем, как переводить числа из десятичной системы счисления в двоичную и как переводить числа из произвольной системы счисления в десятичную. Решим несколько примеров (один ученик выходит к доске, остальные выполняют задание в тетради и сверяются с результатом на доске).
Задание:
Перевести в десятичную систему счисления числа: 1011110012,12313, 1101101012, 12233.
Перевести из десятичной системы счисления в двоичную, и наоборот числа: 256, 457, 845, 1073.
Итог урока.
Фронтальный опрос:
что такое система счисления;
дайте определение понятию «основание системы счисления»;
как перевести число из десятичной системы счисления в двоичную (алгоритм).
Рефлексия/Подведение итогов урока.
-Понравился ли вам урок?
-Было всё понятно?
-Выставление оценок.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Системы счисления (78.5 KB)
Системы счисления (78.5 KB)
 0
0 458
458 3
3 Нравится
0
Нравится
0







