Системы счисления

Системы счисления. Представление чисел ПК

Позиционные системы счисления

• Позиционная система счисления  ( позиционная нумерация ) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).

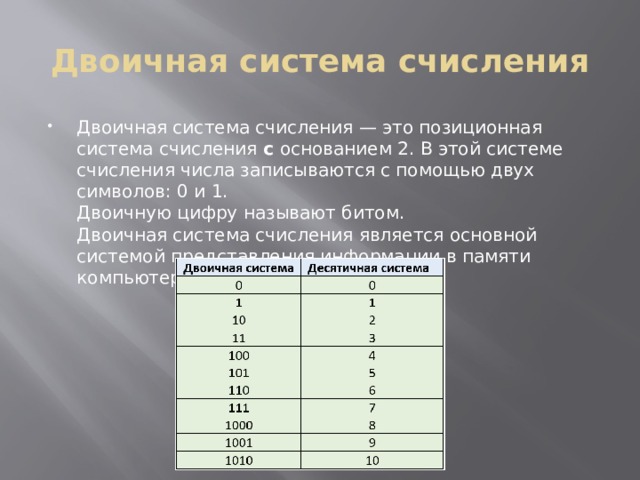
Двоичная система счисления

• Двоичная система счисления — это позиционная система счисления  с основанием 2. В этой системе счисления числа записываются с помощью двух символов: 0 и 1. Двоичную цифру называют битом. Двоичная система счисления является основной системой представления информации в памяти компьютера.

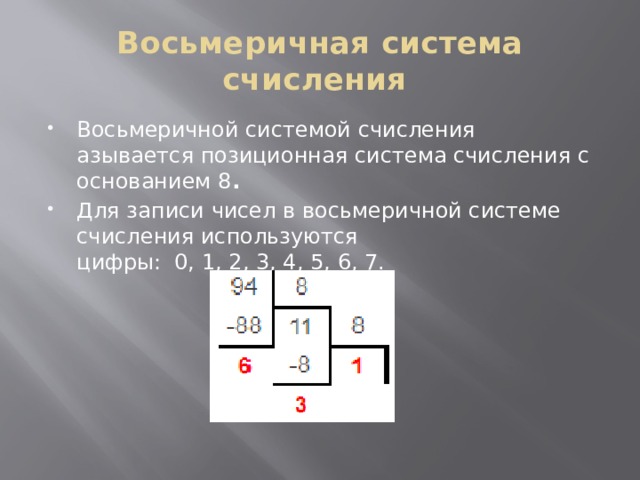
Восьмеричная система счисления 

• Восьмеричной системой счисления   азывается позиционная система счисления с основанием 8 .
• Для записи чисел в восьмеричной системе счисления используются цифры:  0, 1, 2, 3, 4, 5, 6, 7.

Шестнадцатеричная система счисления 

• Шестнадцатеричной системой счисления называется позиционная система счисления с основанием 16.
• Для записи чисел в шестнадцатеричной системе счисления используются цифры:  0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и латинские буквы  A ,  B ,  C ,  D ,  E ,  F . Буквы  A ,  B ,  C ,  D ,  E ,  F  имеют значения 1010, 1110, 1210, 1310, 1410, 1510.

• Вещественное , или  действительное, число  — математический объект, возникший из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких вычислительных операций, как извлечение корня, вычисление логарифмов, решение алгебраических уравнений, исследование поведения функций.

Представление вещественных чисел

• Вещественные числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера.

Арифметические операции

• Арифметические операции принимают в качестве операндов числовые значения (это может быть и литерал и переменная) и возвращают результат в виде одного числового значения. Стандартными арифметическими операциями являются сложение ( + ), вычитание ( - ), умножение ( * ) и деление ( / ).

Представление отрицательных чисел

• Представление отрицательного числа в дополнительном коде
• При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом.

Сложение двоичных чисел

• Сложение одноразрядных двоичных чисел выполняется по следующим правилам:
• 0 + 0 = 0

1 + 0 = 1

• 0 + 1 = 1
• 1 + 1 = 10
• В последнем случае, при сложении двух единиц, происходит переполнение младшего разряда, и единица переносится в старший разряд. Переполнение возникает в случае, если сумма равна основанию системы счисления или больше его (для двоичной системы счисления это не актуально).

Вычитание двоичных чисел

• Вычитание одноразрядных двоичных чисел выполняется по следующим правилам:
• 0 - 0 = 0
• 1 - 0 = 1
• 0 - 1 = 1
• 1 - 1 = 0

Умножение двоичных чисел

• Умножение одноразрядных двоичных чисел выполняется по следующим правилам:
• 0 * 0 = 0
• 1 * 0 = 0
• 0 * 1 = 0
• 1 * 1 = 1

Представление отрицательных чисел в компьютере

• Когда число представляется в формате дополнительного кода, то старший разряд будет считаться определяющим знак. Когда этот разряд равняется нулю, то в остальных разрядах записывается значение, которое совпадает с его основным кодированием. Число, состоящее из восьми разрядов в двоичном коде и имеющее знак, возможно представить в дополнительном коде как некое целочисленное значение в зоне от −128 до +127. Когда старший разряд имеет нулевое значение, то наибольшим числовым значением, которое возможно записать в остальных семи позициях, будет: 2^7-1