Муниципальное бюджетное общеобразовательное
учреждение Горельская СОШ» в с. Малиновка.
Секреты умножения.
Исследовательская работа по математике
Выполнил:
Крец Богдан ученик 6 «ж» класса
филиала МБОУ «Горельская СОШ» в селе Малиновка
Руководитель:
Четырина Зоя Владимировна учитель математики.
Тамбовский район
2020 года
Содержание
Введение. Обоснование выбора темы исследования, цели, задачи работы, актуальность исследования, практическая значимость, методы исследования………………………………………………………............3-5
1. Историческая справка………………………………………………...6
2. Различные способы умножения. …………………………………….7
2.1.Русский «крестьянский способ умножения …………………………7
2.2.Рациональный способ умножения …………………………………..8
2.2.1. Умножение чисел на 22, 33,..99……………………………………..8
2.2.2. Легко запомнить 37 х 3, 37 х 6, 37 х 9…………………………........9
2.2.3. Умножение двузначных чисел с одинаковым числом десятков
и суммой единиц, равной .…....……………………………………………9
2.2.4.Умножение на 9 с помощью пальцев……………………………..9
2.3. Итальянский способ……………..……………………………............10
2.4. Китайский способ…………………...………………………………....11
3. Заключение……………………………………………………………....12
4.Литература………………………………………………………………..13
5.Приложение………………………………………………………………14-16
2
«Предмет математики настолько серьезен,
что полезно не упускать случаев делать
его немного занимательным».
Б. Паскаль
ВВЕДЕНИЕ
Обучаясь в школе, мы понимаем, что нам необходимо знать в совершенствовании не только русский язык, на котором мы говорим, но и математика, которая была и остается одним из основных предметов в школе. Она важна для решения многих жизненных задач: расчеты в магазине, оплата за коммунальные услуги, расчет семейного бюджета и т.д. А чтобы выполнять расчеты, необходимо хорошо знать таблицу умножения, быстро и правильно считать.
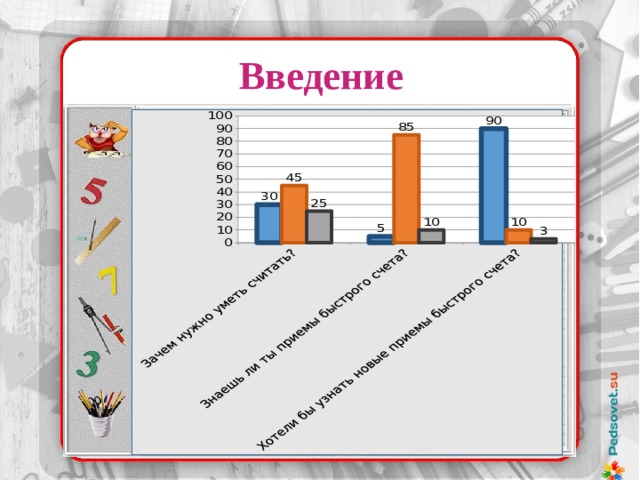
Исследование, проведенное в нашей школе, показало:
Зачем нужно уметь считать?
а) пригодится в жизни, например, считать деньги(45%); б) чтобы хорошо учиться в школе (30%); в) чтобы быть грамотным (25%); д) не обязательно уметь считать (0%).
2. Перечислите, при изучении, каких школьных предметов тебе понадобится правильно считать?
а) математика (90%); б) физика (5%) в) химия (5%);
г) обществознание(0%).
3.Знаешь ли ты приемы быстрого счета?
а) да, много (5%); б) да, несколько (70% - 2 способа); в) нет, не знаю(25%).
4. Хотели бы вы узнать приемы быстрого счета, чтобы быстро считать?
а) да (90%); б) нет (10%).
Исследование показало, проблема заключается в ограниченном числе способов умножения натуральных чисел школьной программы, а так же интерес учащихся (90%) освоить новые приемы быстрого счета.
3
Актуальность. Тема для исследования выбрана не случайно. В последнее время ребята всё с большей неохотой относятся к учёбе, и в частности к математике. Есть ученики, которые не знают даже таблицы умножения! Поэтому доверяют гаджетам больше чем себе. Это снижает качество знаний по очень важному предмету как математика. Чтобы привлечь внимание учащихся к математике, выбрал тему «Секреты умножения». Она позволит не только заинтересовать обучающихся, но и контролировать, оценивать, находить и исправлять ошибки в результате механизированных вычислений.
Поставлена цель работы: выявление необычных способов умножения, отличных от школьной программы.
Для достижения поставленной цели, определены основные задачи:
изучить и проанализировать специальную литературу по проблеме исследования;
изучить историю развития умножения натуральных чисел;
найти как можно больше необычных способов вычислений;
рассказать о новых способах умножения и научить одноклассников ими пользоваться;
Объект исследования: математическое действие умножения
Предмет исследования: необычные способы умножения
Характер исследования обуславливает необходимость применения комплекса следующих общенаучных методов исследования:
поисковый метод с использованием научной и учебной литература, а также поиск необходимой информации в сети Интернет;
исследовательский метод при определении способов умножения;
практический метод при решении примеров.
Гипотеза: изучив новые необычные способы умножения, можно внедрить их в собственную вычислительную практику.
Практическая значимость исследования.
4
Материал данного исследования могут использовать обучающиеся для отработки навыков быстрого счета.
Говорят, если хотите научиться плавать, вы должны войти в воду, а если хотите уметь решать задачи, то должны начать их решать. Но для начала надо освоить азы арифметики. Научиться считать быстро, можно только при большом желании и систематической тренировке в решении задач.
Компенсировать недостаток знаний удалось за счёт изучения дополнительной научной литературы и знакомства с новыми методами умножения чисел.
5
СОДЕРЖАНИЕ.
1.Историческая справка.
В древности на Руси говорили: «Умножение – мучение, а деление – беда».
Считается, что таблица умножения впервые была изобретена в Месопотамии. Эта теория подтверждается находками археологов. Самая старейшая табличка была найдена на раскопках древнего Вавилона и имеет возраст около 4000 лет. Внешне это — глиняная дощечка с клинописью.
Не так давно при раскопках здания в городе Нара, древней столице Японии (8 век), архиологами была найдена деревянная табличка с фрагментом таблицы умножения. К сожалению, в настоящее время ученые точно не могут ответить на вопрос о происхождении таблички, но установлено, что ее активно использовали в Китае еще 2700 лет назад. По одной из версий, таблица умножения была изобретена в Индии и затем попала в Европу, а по другой версии, в Индию она попала из Китая.
Таблицу умножения также называют «Таблицей Пифагора», особенно когда она представлена в виде квадрата, стороны которого — множители, а в ячейках стоит их произведение.
Известно, что впервые таблица умножения была введена в школах в средневековой Англии. Выглядела она как система перемножения чисел до 12.
В Россию современная таблица умножения попала благодаря математику Леонтию Филипповичу Магницкому, который в 1707 году издал первый учебник по математике под названием «Арифметика». В этом учебнике были таблицы сложения и умножения.
6
2. Различные способы умножения.
2.1.Русский «крестьянский» способ умножения.
В России 2-3 века назад среди крестьян некоторых губерний был распространен способ, который не требовал знание всей таблицы умножения. Это – иной способ умножения, истинное происхождение которого пока не установлено. И этот способ умножения называют: русский «крестьянский» способ умножения. Надо было лишь уметь умножать и делить на 2. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат.
Алгаритм решения для нечетных чисел:
пишем оба числа на одной прямой и рисуем между ними вертекальную прямую;
число с левой стороны делим на 2, а с правой — умножаем на 2. Подобную манипуляцию проводим до момента, пока слева не останется 1;
необходимо вычеркнуть строки, где слева стоят четные числа;
числа, которые остались справа складываем и получаем результат.
Пример 1. Умножение чисел 37х26 (приложение 1).
Пример 2. Умножение чисел 47х35.
Вывод: данное умножение не является копией каких-либо известных на сегодня способов умножения, поэтому заслуживает особого внимания.
Плюсы: знать только умножение и деление на 2.
Минусы: затрачивается большее количество времени, чем на умножение в столбик.
7
2.2.Рациональный способ умножения.
Рациональных способов умножения существует несколько десятков. В данной работе рассмотрим несколько способов умножения, возможно, они покажутся более простыми, и вы будете ими пользоваться.
2.2.1.Умножение чисел на 22, 33, … , 99.
Чтобы двузначное число умножить на 22, 33, ..., 99, надо этот множитель представить в виде произведения однозначного числа (от 2 до 9) на 11, то есть 44 = 4 х 11; 55 = 5 х 11 и т.д. Затем произведение первых чисел умножить на 11 (данный способ был рассмотрен).
Пример 3. Умножить числа 18 х 22 = 18 х 2 х 11 = 36 х 11 = 396
Пример 4. 18 х 33 = 18 х 3 х11 = 54 х 11 = 594.
Птимер 5. 18 х 44 = 18 х 4 х 11 = 72 х 11 = 792.
2.2.2. Легко запомнить 37 х 3, 37 х 6, 37 х 9…
Умножая число 37 на 3 получаем 111, (37 х 6 = 222, 37 х 9 = 333,…) зная правила умножения двузначного числа на число 11, легко можно умножить и на 111, 1111,…
Если сумма цифр первого множителя меньше 10, надо мысленно раздвинуть цифры этого числа на 2, 3 и т.д. шага, сложить цифры и записать соответствующее количество раз их сумму между раздвинутыми цифрами. Количество шагов всегда меньше количества единиц на 1.
Пример 6. 24х111=2(2+4) (2+4)4=2664 (количество шагов - 2)
Пример 7. 24х1111=2(2+4)(2+4)(2+4)4=26664 (количество шагов - 3)
Эти вычисления можно легко произвести в уме.
Умножение двузначного числа на 111, 1111, 1111 и т.д., сумма цифр которого равна или больше 10. В этом случае к цифре стоящей впереди нужно прибавить 1.
Пример 8. 48 х 111 = 4 (4+8) (4+8) = 4 (12) (12) 8 = (4+1) (2+1) 28 = 5328.
8
2.2.3. Умножение двузначных чисел с одинаковым числом десятков и суммой единиц, равной 10.
Алгоритм умножения следующий:
десятки первого числа умножаем на десятки второго, предворительно увеличив его на один;
переумножаем единицы первого и второго числа;
к полученному результату первого действия дописываем результат второго действия.
Пример 9. 62*68=4216
1)6*7=42
2)2*8=16.
Пример 10. 84*86=7224
1)8*9=72
2)4*6=24
2.2.4. Умножение на 9 с помощью пальцев.
Считаю, что умножение на 9 дается для некоторых обучающихся нелегко. Однако именно для числа 9 умножение легко воспроизводится "на пальцах". Для этого нужно повернуть руки ладонями от себя. Мысленно присваивается пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки.
Допустим, нам надо умножить 3 на 9. Чтобы вычислить ответ, надо найти палец под номером 3 и загнуть его. Количество пальцев слева от загнутого пальца – это десятки, количество пальцев справа – это единицы. У нас слева – 2 пальца, это 2 десятка, а справа 7 пальцев. Значит, 3·9=27.
Вывод: владение навыками рационального способа упрощает вычисления, экономит время, тренирует память, развивает математическое логическое мышление, является залогом успешной учебы;недостаток данного способа в том, что не всегда его можно применить.
9
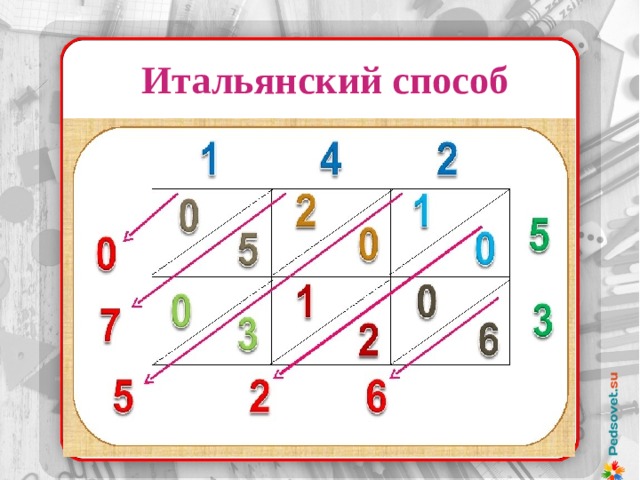
2.3. Итальянский способ умножения (“Сеткой”)
В Италии, а также во многих странах Востока, этот способ приобрел большую известность.
Этим способом пользовались ещё в древности, в Средние века он широко распространился на Востоке, а в эпоху Возрождения — в Европе. Способ решётки именовали также индийским, мусульманским или "умножением в клеточку". А в Италии его называли "джелозия", или "решётчатое умножение" (gelosia в переводе с итальянского — "жалюзи", "решётчатые ставни"). Действительно, получавшиеся при умножении фигуры из чисел имели сходство со ставнями-жалюзи, которые закрывали от солнца окна венецианских домов.
Алгоритм умножения:
вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте;
умножаем число каждого ряда последовательно на числа каждой колонки. Если при умножении получается однозначное число, записываем вверху 0, а внизу это число;
заполняем всю сетку и складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.
Пример 10. Умножить 142 х 53 (приложение 2).
Вывод: считаю, способ решётки ни в чём не уступает умножению столбиком. Он даже проще и надёжнее. Во-первых, работать приходится только с однозначными и двузначными числами, а ими легко оперировать в уме. Во-вторых, не требуется запоминать промежуточные результаты и следить за тем, в каком порядке их записывать. Память разгружается, а внимание сохраняется, поэтому вероятность ошибки уменьшается. К тому же способ решётки позволяет быстрее получить результат.
10
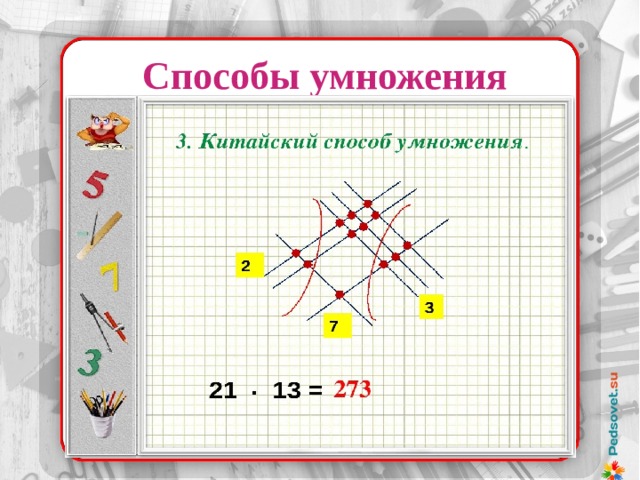
2.4.Китайский способ.
Ученые выделяют более 27 способов умножения в разных странах, но китайский метод считается одним из самых древних. Китайская таблица умножения также использовалась в астрономических расчетах, а научная основа была сформирована в 17 веке после начала активного взаимодействия с европейскими учеными. Интересно, что здесь параллельно происходило развитие практической математической школы и арифмологии, нацеленной на изучение значений чисел.
Алгоритм умножения;
рисуем с помощью линий первую цифру горизонтально;
рисуем снизу с помощью линий вторую цифру горизонтально;
рисуем слева направо вертикально первую цифру второго множителя;
рисуем справа вторую цифру второго множителя;
делаем подсчет количества точек пересечений горизонталей и вертикалей, после чего выделяем из них три части - верхнюю левую, нижнюю правую и комбинированную, куда входят верхние правые и нижние левые точки;
формируем ответ, собирая цифру с учетом того, что первая зона соответствует единицам, вторая – десяткам (числа суммируются), третья – сотням;
получаем искомый ответ (приложение 3).
Вывод:
достоинства умножения небольших двузначных чисел — простота их выполнения и наглядность;
недостаток - большие числа.
11
ЗАКЛЮЧЕНИЕ
Гипотеза подтвердилась, все рассмотренные новые необычные способы умножения можно и нужно применять на практике, чтобы развить скорость вычисления, добиться успехов в изучии школьных предметов. Больше всего мне понравился счет на пальцах и индийский способ. Эти способы понравились не только мне, но и моим однаклассникам.
Следующая задача освоить самый современный способ умножения, который разработал кандидат филосовских наук Василий Иванович Оконешников. Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.
Думаю, что наш способ умножения в столбик не является совершенным и можно придумать еще более быстрые и более надежные способы.
Как мы видим, быстрый счёт это уже не тайна за семью печатями, а научно разработанная система. Раз есть система, значит, её можно изучать, ей можно следовать, ею можно овладевать.
12
Литература
Мартин Гарднер Математические новеллы. – М.: Мир, 1974 для 9 на пальцах
Мартин Гарднер Математические новеллы. – М.: Мир, 1974 для 9 на пальцах
Олехник С. Н., Нестеренко Ю. В., Потапов М. К. «Старинные занимательные задачи». – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с
Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941 — 12 с.
Перельман Я.И. Занимательная арифметика. М.Русанова,1994–205с.
Интернет – ресурсы
1.Быстрое умножение без калькулятора. http://samoychka.ru
2.Как научиться быстро считать в уме. http://kanks.ru/
3. https://moluch.ru/young/archive/9/633/
2ринять во внимание, что
19 Г— 17 = (18 + 1) 17= 18 Г— 17 + 17 9 Г— 34 = (8 + 1) 34 = 8 Г— 34 + 34 и т2. п.
Ясно, что числа – 17, 34 и т. п., утрачиваемые при делении нечетного числа пополам, необходимо прибавить к результату последнего умножения, чтобыолучить произведение. Нельзя, как видите, отказать в практично
13
Приложение №1.
Пример 1.
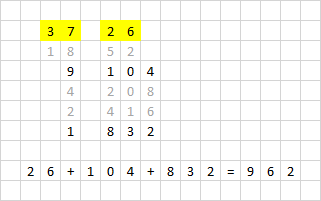

(рис.1)
14
Приложение №2.
Итальянский способ умножения
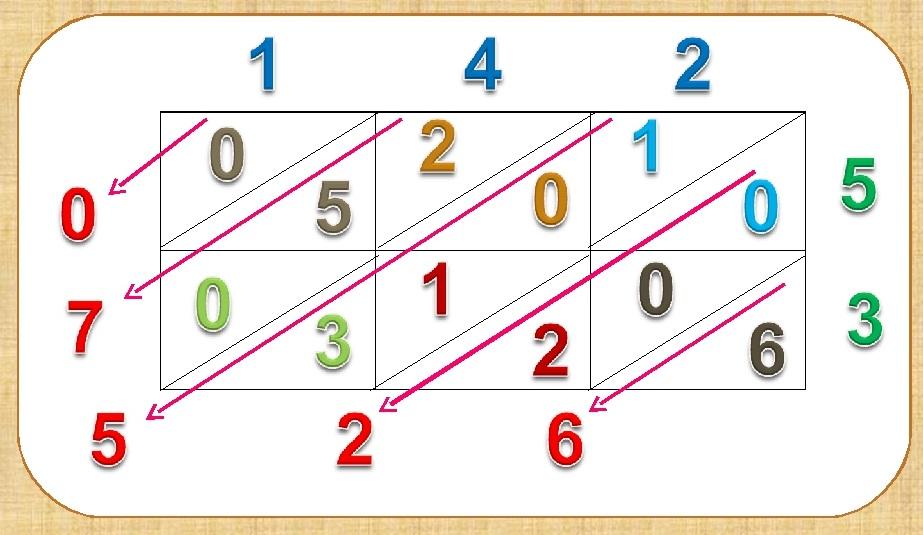
(рис 2).
15
Приложение №3.
Китайский способ умножения
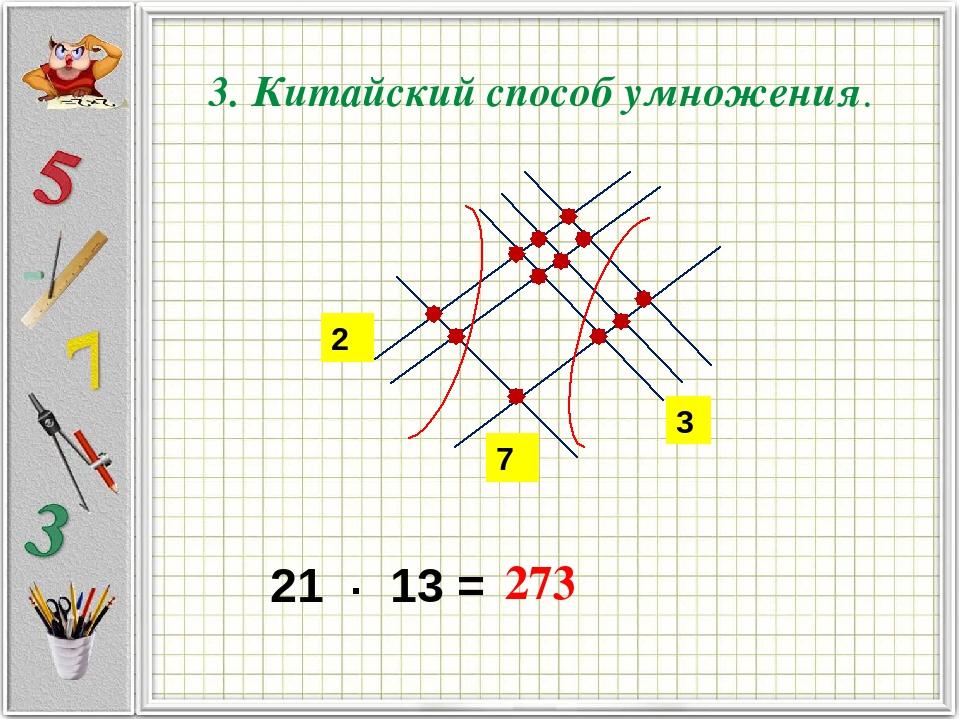
(рис 3)
16

 Получите свидетельство
Получите свидетельство Вход
Вход








































 Секреты умножения (2.55 MB)
Секреты умножения (2.55 MB)
 0
0 542
542 7
7 Нравится
0
Нравится
0






