Сборник заданий по теме
«Степени и корни»
Оглавление
Аннотация
Теоретический материал
Упражнения по теме « Степени и корни»
Аннотация
В данной разработке предложен материал, касающийся степеней и корней. Даны основные определения, сформулированы свойства.
Приведены примеры заданий различной сложности: арифметические задания на вычисление значений выражений с корнями и степенями, алгебраические задания на преобразование выражений, решение уравнений и неравенств.
Рассматриваемые вопросы широко применяются в алгебре и часто используются при подготовке к итоговой государственной аттестации.
Данная тема не является самой сложной в курсе алгебры. Однако при выполнении заданий встречается много ошибок.
Использование данных упражнений поможет закрепить умения и углубить знания по данной теме.
Основные определения и теоремы.
Истоки понятия степени находятся в глубокой древности; дошедшие до нас глиняные плитки древних вавилонян содержат записи таблиц квадратов, кубов и их обратных значений.
Первоначально под степенью понимали произведение нескольких одинаковых сомножителей. Способы записи степеней и связанных с ними обратных величин – корней из числа менялись с течением времени, пока не приняли современную форму.
Дальнейшее развитие науки вызвало необходимость расширения степени. В XIV в. Французский епископ города Лизье в Нормандии Н. Орем (1323-1382гг.) впервые стал заменять в отдельных случаях корни из чисел дробными показателями степени и ввёл символические обозначения степени с дробными показателями. Например, 8 как 41,5. Показатели, введённые Оремом, по существу выступают в виде логарифмов чисел. Орем словесно сформулировал правила для выполнения различных операций со степенями.
Значительно позднее бухгалтер из Брюгге, а впоследствии военный инженер С. Стевин (1548-1620) вновь открыл дробные показатели и указал в более общем виде, что корень энной степени из числа а можно выразить как а1/n, где а0.
Степенью с нулевым показателем первым стал пользоваться самаркандский учёный ал-Каши в начале XV в. Независимо от него Н. Шюке в работе «Наука о числах в трёх книгах» в 1484 г. применял нулевой и отрицательный показатели.
Завершили введение современного изображения степени англичане Джон Валлис и Исаак Ньютон.
Обобщение понятия степени аn, где n- любое действительное число, позволило рассматривать показательную функцию (y=ax) на множестве действительных чисел и степенную функцию (y=xn) на множестве положительных чисел, а при целых n степенная функция определена и для x
Теоретический материал
Пусть дано положительное число а и произвольное действительное число п. Число ап называется степенью,
число а – основанием степени, число п – показателем степени.
По определению полагают: а1 = а,
а0 = 1,
а-п = 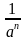 , п
, п  R
R
Если а – положительное число, т – целое число, а п – натуральное число и п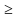 2, то
2, то  =
= 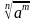 .
.
Свойства степени. Если а и в – положительные числа, х и у – любые действительные числа, то справедливы
следующие свойства: ах ау = а х + у,
ах : ау = а х - у,
(а х) у = а х у,
ах в х = (а в) х,
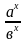 = (
= ( )х.
)х.
Пусть п – натуральное число, отличное от единицы, а – неотрицательное число.
Арифметическим корнем п –й степени из неотрицательного числа а называется неотрицательное число, п – я степень которого равна а.
Для арифметического корня п- й степени из неотрицательного числа а используется обозначение  . Если п=2, пишут
. Если п=2, пишут  . По определению
. По определению
( )п = а.
)п = а.
Для любых, в том числе отрицательных, значений, а справедлива формула  = /а/, в частности,
= /а/, в частности,
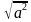 = /а/ и
= /а/ и 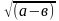 2 = /а – в/.
2 = /а – в/.
Свойства арифметического корня.
Если а и в – неотрицательные числа, п и к – натуральные числа, отличные
от единицы, т –целое число, то имеют место следующие соотношения:
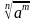 = (
= (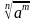 ),
),
 =
= 
 ,
,
 =
= 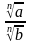 , b неравно 0,
, b неравно 0,
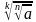 =
= 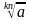 ,
,

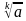 =
= 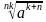 ,
,
 :
: 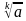 =
= .
Степень с дробным показателем.
Если а – положительное число, т – целое число, а п – натуральное число и
п 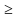 2, то
2, то  =
= 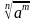 = (
= ( m.
Управжнения.
Вычислить:
1) ; 5)
;
2) ; 6)
;
3) ; 7)
, если
,
;
4) ; 8)
, если
,
.
Упростить:
1) ; 3) ;
2) ; 4) .
Решить графически уравнения:
1) ; 3)
;
2) ; 4)
.
Извлечь арифметический корень:
1) ; 4)
;
2) ; 5)
;
3) ; 6)
.
Вычислите степени с рациональным показателем:
|
| a | b | c | d | e | f | g | h |
| 1 | 34 | 43 | 24 | 53 | 25 | 33 | 50 | 23 |
| 2 |
|
|
|
|
|
|
|
|
| 3 | 6-2 | 2-4 | 3-3 | 5-1 | 3-4 | 2-3 | 7-2 | 4-1 |
| 4 |
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
| 6 |
|
|
|
|
|
|
|
|
| 7 |
|
|
|
|
|
|
|
|
| 8 |
|
|
|
|
|
|
|
|
Вычислите:
,
,
,
,
,
2 -
+
,
,
1,70+ 32:3-1 – 251/2 , 163/4 – 71,7:7-0,3 + 430,
- 0,43 0,4-2
52 +160,5, (
)2
1,4 + 1251/3 – (
)-1,
811/4 9-1/2 + 13,40 –(52)-1 , 641/3:90,5 – 35,2
3- 6,2 +5,20,
(641/3 272/3
2432/5
128 3/7 )1/
(62,5 36 -1)4 - ( 51/4
253/8) sin П/ 2.
Найдите значение выражения:
,
+
-
-
, 0,3
-0,1,
+
,
,
:
,
, .
Найдите значение выражения:
, при п = 8,
46Р 4 -4Р , при р =
,
- , при х = 7,
, при х =16,
+
, при р = 49,
-
, при р =16, q = 9,
+
, при х = 16, у = 25,
-
, при х = 9, у = 49,
+
, при а = 625, в = 16,
- 2
, при а = 9, в =16.
Решить иррациональные уравнения и системы иррациональных уравнений
Решите уравнения:
1)
=6; 2)
; 3)
4) ; 5)
; 6)
Решить систему уравнений.
Задания по решению уравнений:
75х+6 = 49, ( )0,5х – 1 = 4, (
)1 – 3х = 9,
2-х = ( )1-х, 3х = (
)1 + х, 10-х =
,
3х2 -5х+1 = 81, = 0,125 х-7 , 53х-1
23х-1 =
0,1 ,
2 х+2 – 2 х = 96, 5 7 х-1 + 4
3 х + 3 х+1 - 2
7 х = 0, 4 х - 10
2 х-1 = 24,
9 х – 3 х-1 = 6, 4 х + 3 6 х – 4
9 х = 0, 2 х-1 + 2 –х-1 = 1.
Задания по решению неравенств:
16 2 х+3, 2 5х+7
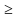 8 х, 2 х
8 х, 2 х -
,
5 х
, 2
4 х+1
2 –х -1 , 3
9 х+1
3 – х – 1
9 х - 9 3 –х
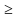 0, 7 х - 7
0, 7 х - 7 7 – х -2
0, (
) х - 8
2 – х
0,
х+1, (
) х+2+4/ х
, 2 х+1 + 3
2 х
10,
9 х – 3 х+1 4, 2 х – 2 1-х
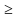 1, 9 х - 5
1, 9 х - 5 6х - 6
4 х
0.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Сборник заданий (124.98 KB)
Сборник заданий (124.98 KB)
 0
0 7970
7970 446
446 Нравится
0
Нравится
0






