Самостоятельная работа "Третий признак равенства треугольников"

Вариант 1

Дано: АD = АВ и 1 = 2

АВС = 108°, АСВ = 32°.

Докажите: Δ АDС = Δ АВС

Найдите: углы АDС и АСD

Вариант 2

B

1

A

Дано: АВ = DС и 1 = 2.

АВС = 102°, ВСА = 38°.

Докажите: Δ АDС = Δ АВС

Найдите: углы АСВ и АDС

Самостоятельная работа

Выберите вариант:

1

2

Вариант1

1.

Найдите BD и AB, если AC=12см, DC=8см.

2. Отрезки AC и BD точкой пересечения делятся пополам. Докажите, что

B

1

D

A

2

C

Вариант2

1.

Найдите BD и AB, если AC=17см, DC=5см.

2. Отрезки PC и QD точкой пересечения делятся пополам. Докажите, что

B

1

A

D

2

C

Самостоятельная работа

Выберите вариант:

1

2

Вариант 1

1  . На рисунке 11 AB=DF ,  A =  F и AB=FE . Будут ли данные треугольники равны?

2  . Отрезки GH и RS пересекаются в точке H и делятся в ней пополам. Найдите отрезок RH , если SG =11,5 см.

3. На рисунке 12 найдите пары равных треугольников.

4. Докажите, что прямая, отсекающая от сторон угла равные отрезки, перпендикулярна его биссектрисе.

5*. На продолжении каждой стороны правильного треугольника ABC отложены равные отрезки, а именно AA 1 = BB 1 = CC 1 . Докажите, что треугольник A 1 B 1 C 1 тоже правильный. Сделайте соответствующий рисунок.

6*. Треугольник, периметр которого равен 12 см, делится высотой на две части, периметры которых равны 7 см и 9 см. Найдите данную высоту.

Вариант 2

1  . На рисунке 11 AB=EF , CB=DE и  B =  E . Будут ли данные треугольники равны?

2  . Отрезки TU и VW пересекаются в точке X и делятся в ней пополам. Соедините концы отрезков и найдите равные треугольники.

3. На рисунке 13 найдите пары равных треугольников.

4. На сторонах угла G отложены равные отрезки GA , GC и проведена его биссектриса, на которой отмечена точка B . Докажите, что BG является биссектрисой угла ABC .

5*. На каждой стороне правильного треугольника XYZ отложены равные отрезки, а именно XX 1 = YY 1 = ZZ 1 . Докажите, что треугольник X 1 Y 1 Z 1 тоже правильный. Сделайте соответствующий рисунок.

6*. Периметр треугольника CDE равен 21 см. Из вершины D выходят равные стороны. Медиана CM делит треугольник на два треугольника, причем один из них имеет периметр на 3 см больше, чем другой. Найдите стороны данного треугольника.

Самостоятельная работа

Выберите вариант:

1

2

Вариант 1

1. Сформулировать и доказать теорему, выражающую первый признак равенства треугольников.

2 .Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?

3 .Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?

4. Сформулировать теорему об углах равнобедренного треугольника.

Задача №1 BO=OC, .

Укажите равные

треугольники на этом рисунке

Вариант 2

1. Сформулировать и доказать теорему, выражающую второй признак равенства треугольников.

2.Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?

3.Какой треугольник называется равнобедренным? Как называются его стороны?

4.Сформулировать теорему о биссектрисе равнобедренного треугольника.

Задача №1

,

Укажите равные

треугольники на этом

рисунке.

Самостоятельная работа

Выберите вариант:

1

2

Вариант 1

1. На рисунке BD = АС,

ОВ = ОС.

Докажите, что

2. Н а рисунке OA=OC и

Докажите

3. На рисунке AB=BC, AK=KC,

Докажите, что

Вариант 2

• На рисунке OA =O С,

Докажите, что

2. Н а рисунке OA=OC и

Докажите

3. На рисунке AB=BC ,AM=PC,

Докажите, что

Самостоятельная работа «Второй признак равенства треугольников»

Выберите вариант:

1

2

Вариант 1

1  . На рисунке 14 определите равные треугольники.

2  . Какие треугольники на рисунке 15 равны?

3. Есть ли на рисунке 16 равные треугольники?

4. На рисунке 17  1=  2,  3=  4. Докажите равенство  5 и  6.

5*. Изобразите два неравных треугольника, у которых имеется по две равные стороны и одному равному углу.

6*. Проведите прямую, имеющую общие точки со всеми сторонами данного треугольника.

Вариант 2

1  . На рисунке 18 определите равные треугольники.

2  . Какие треугольники на рисунке 19 равны?

3. Есть ли на рисунке 20 равные треугольники?

4. Треугольники RST и R 1 S 1 T 1 равны (рис. 21). Отрезки SQ и S 1 Q 1 образуют равные углы со сторонами треугольников соответственно RS и R 1 S 1 . Докажите равенство отрезков TQ и T 1 Q 1 .

5*. Изобразите два неравных треугольника, у которых имеется по два равных угла и одной равной стороне.

6*. Докажите, что нельзя провести прямую таким образом, чтобы она пересекала все стороны треугольника по внутренним точкам.

Самостоятельная работа «Третий признак равенства треугольников»

Выберите вариант:

1

2

Вариант 1

1  . Докажите, что на рисунке 26  B=  D .

2  . На рисунке 27 укажите пары равных треугольников.

3. На рисунке 28 укажите пары равных треугольников.

4. Докажите, что если в треугольнике высота делит сторону, к которой она проведена, пополам, то треугольник равнобедренный.

5*. На одной стороне угла P отложены отрезки PA и PB . На другой его стороне отложены отрезки PA 1 = PA и PB 1 = PB . Докажите, что прямые AB 1 и A 1 B пересекаются в точке, принадлежащей биссектрисе данного угла P .

6*. Найдите в треугольнике XYZ на стороне XY или на ее продолжении точку M , одинаково удаленную от вершин X и Z . Отметьте особый случай.

Вариант 2

1  . Докажите, что на рисунке 29  H=  G .

2  . На рисунке 30 укажите пары равных треугольников.

3. На рисунке 31 укажите пары равных треугольников.

4. Докажите, что если в треугольнике медиана перпендикулярна к стороне, которую она делит пополам, то треугольник равнобедренный.

5*. Докажите, что перпендикуляры, проведенные к обеим сторонам угла на равных расстояниях от вершины, пересекаются на его биссектрисе.

6*. Каждая из точек X и Y одинаково удалена от точек S и T . Определите положение прямой XY по отношению к отрезку ST .

Самостоятельная работа «Равнобедренный треугольник»

Выберите вариант:

1

2

Вариант 1

1  . Основание равнобедренного треугольника равно 16,3 см. Найдите другие стороны треугольника, если его периметр равен 40,5 см.

2  . Боковые стороны равнобедренного треугольника каждая больше в 2 раза его основания. Найдите стороны треугольника, если его периметр равен 44 см.

3. В треугольнике CDE (рис. 22) DH  CE , CH=EH . Докажите, что треугольник равнобедренный.

4. На рисунке 23 RT – основание равнобедренного треугольника SRT ,  1=  4 и SH  RT . Докажите: а)  6=  7; б) RM=TN ; в)  1=  4.

5*. Периметр равнобедренного треугольника ABC равен 44 см. Из вершины C его основания AC проведена медиана CM . Найдите стороны данного треугольника, если периметр треугольника BCM на 8 см меньше периметра треугольника ACM .

6*. Сколько равнобедренных треугольников изображено на рисунке 24, где A 1 A 2 A 3 A 4 A 5 – правильный пятиугольник?

Вариант 2

1  . Боковая сторона равнобедренного треугольника равна 13 см, а основание меньше ее на 0,85 см. Найдите периметр треугольника.

2  . Основание равнобедренного треугольника на 0,7 см больше его боковой стороны. Найдите стороны треугольника, если его периметр равен 25 см.

3. На рисунке 25  1=  2. Определите вид треугольника KLM .

4. На рисунке 23 SM=SN , SH  MN и RM=TN . Докажите: а)  2=  3; б)  1=  4; в) SR=ST .

5*. В равностороннем треугольнике ABC сторона AC продолжена за вершину C и на продолжении отложен отрезок CD . Точка D соединена с вершиной B треугольника. Найдите периметр данного треугольника, если известно, что периметр треугольника BCD на 15 см меньше периметра треугольника ABD .

6*. Сколько различных типов равных равнобедренных треугольников изображено на рисунке 24, где A 1 A 2 A 3 A 4 A 5 – правильный пятиугольник?

Разноуровневая самостоятельная работа

Выберите уровень задания:

1 уровень

2 уровень

3 уровень

Выберите вариант:

1 вариант

2 вариант

Самостоятельная работа. Признаки равенства треугольников

1.

Дано: AB = CD , BC = AD , .

2. В треугольниках АВС и : , , . Точки D и D 1 лежат соответственно на сторонах AC и A 1 C 1 , .

I вариант

Докажите , что: а) ΔABD = ΔA 1 B 1 D 1

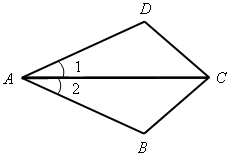
Доказать: ΔABD=ΔCDB

б) .

Найти: .

Самостоятельная работа. Признаки равенства треугольников

1.

Дано: AB = AD , ,

2. В треугольниках АВС и : , , . Точки D и D 1 лежат соответственно на сторонах AC и A 1 C 1 , , .

II вариант

Докажите , что: а)

б)

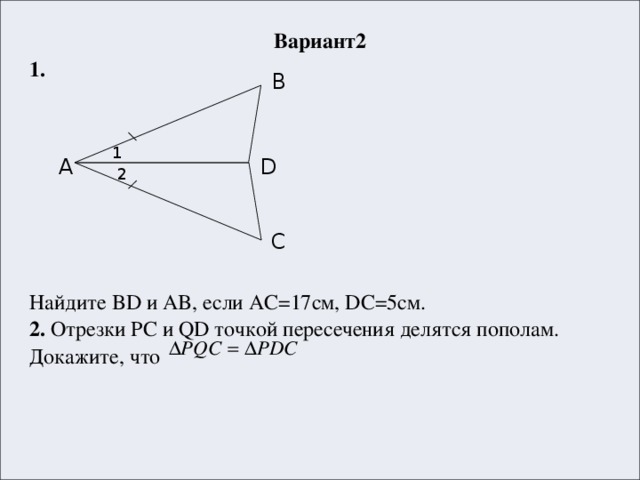
Доказать: ΔADC = ΔABC

Найти:

ΔABD = ΔA 1 B 1 D 1

Выберите вариант:

1 вариант

2 вариант

Самостоятельная работа. Признаки равенства треугольников

1.

Дано: AB = CD , BC = AD .

2. В треугольниках АВС и : , , .

I вариант

Отрезки AD и -биссектрисы данных треугольников.

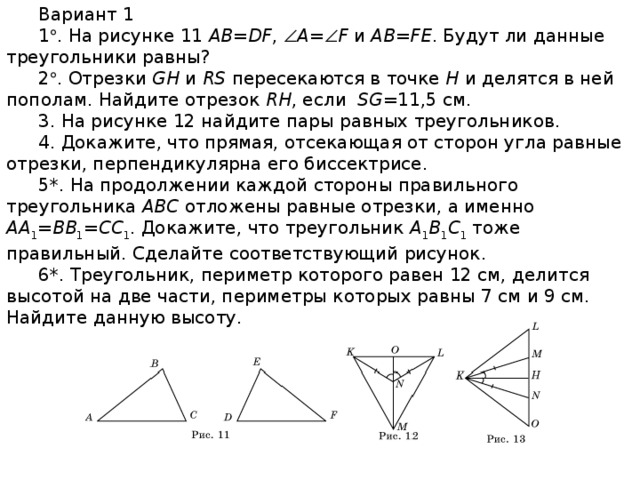
Доказать:

Докажите , что .

ΔABD = ΔA 1 B 1 D 1

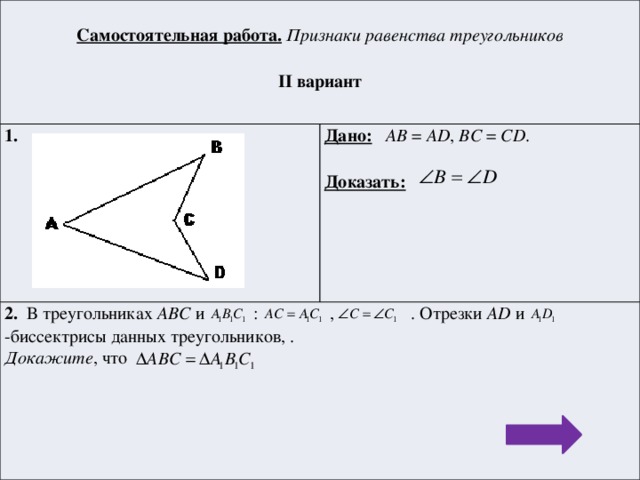
Самостоятельная работа. Признаки равенства треугольников

1.

Дано: AB = AD , BC = CD .

2. В треугольниках АВС и : , . Отрезки AD и -биссектрисы данных треугольников, .

II вариант

Докажите , что

Доказать:

Выберите вариант:

1 вариант

2 вариант

Самостоятельная работа. Признаки равенства треугольников

1.

Дано: AB = CD , АC = BD .

2. ΔMNP - равнобедренный с основанием MP , точка К – середина отрезка МР . Точки E и F лежат на сторонах MN и N P ΔMNP соответственно, МЕ = PF .

I вариант

Докажите , что луч KN – биссектриса угла ЕКF.

Доказать:

Самостоятельная работа. Признаки равенства треугольников

1.

Дано: AB = CD , АC = BD .

2. ΔMNP - равнобедренный с основанием MP , точка К – середина отрезка МР . Точки E и F лежат на сторонах MN и N P ΔMNP соответственно, .

II вариант

Докажите , что ΔNEK = ΔNFK .

Доказать: