Муниципальное бюджетное общеобразовательное учреждение
Васильевская средняя общеобразовательная школа
«Рассмотрено» «Согласовано» «Утверждаю»
На ШМО учителей Заместитель директора Директор МБОУ
математики школы по УВР Васильевской сош
__________Кузьмина Н.Н. __________Харлова Н.А. _________ Пылёва Е.Н.
Протокол № __ Приказ №___
от «__» ________20___г. от «__»________20___г. от «__»________20___г.
Рабочая программа элективного курса «Решение задач с параметрами».
10 класс.
| Разработала:
| В.Н.Оленич учитель математики
|
2017-2018 учебный год
Пояснительная записка.
Элективный курс «Решение задач с параметрами» 10 класса предусматривает ознакомление учащихся с методами решений задач с параметрами. Как известно, решению задач с параметрами в школе уделяется очень мало внимания.. Запланированный данной программой для усвоения учащимися объем знаний необходим для овладения ими методами решения задач с параметрами, а точнее уравнений и неравенств с параметрами, что открывает перед учащимися значительное число эвристических приёмов общего характера, ценных для математического развития личности, применимых в исследованиях и на любом другом математическом материале
Целью данного курса является проверить знания основных разделов школьной математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности.
По-моему мнению, такой диагностической и прогностической ценностью в полной мере обладают задачи с параметрами. Далеко не случайно эти задачи стали неотъемлемым атрибутом экзаменационных билетов многих институтов.
Весь материал курса помимо деления на главы и параграфы разбит на пункты. Каждый пункт посвящён определённому типу задач или приёму их решения. Упражнения для самостоятельной работы приводятся сразу после соответствующего пункта.
Итак, данный курс имеет прикладное и общеобразовательное значение, способствует развитию логического мышления учащихся. Используются традиционные формы организации занятий, такие как лекция и семинар. Богатство и разнообразие примеров и подходов к решению одного и того же примера позволит учащимся проявить себя, лучше понять математику как предмет.
За основу взяты: Подробная авторская программа элективного курса «Алгебраические задачи с параметрами» учителя математики сош №52 Л.В.Гладышевой г. Липецк, программа «Алгебра плюс: Элементарная алгебра с точки зрения высшей математики» - тема 6; «Алгебраические задачи с параметрами» - автор А.Н.Земляков)
Цель курса:
создать целостное представление о параметрах, формировать и развивать у учащихся творческие способности, интеллектуальные и практические умения в области решения задач с параметрами, тем самым обеспечить качественную подготовку к выпускным экзаменам и вступительным экзаменам в ВУЗы.
Задачи курса:
активизировать познавательную деятельность школьников;
путем создания проблемных ситуаций помочь учащимся углубить знания о параметрах;
создавать положительную мотивацию обучения на выбранном профиле;
повышать информационную компетентность обучающихся;
обобщить и совершенствовать знания учащихся по теме «Решение задач с параметрами» в процессе подготовки к сдаче ЕГЭ по математике.
обеспечить педагогические условия для расцвета личности школьника, его творческого потенциала.
Общая характеристика курса
Этот элективный курс представляется актуальным, поскольку заданиям с параметрами в школьной программе не уделено достаточного внимания, хотя они ежегодно предлагаются как на школьных выпускных экзаменах, так и на вступительных экзаменах в ВУЗы, зачастую являясь границей, отделяющей непроходную четверку от проходной пятерки. Задачи с параметрами требуют к себе своеобразного подхода – здесь необходимо грамотное и тщательное исследование, высокая логическая культура, поэтому процесс обучения строится как совместная исследовательская деятельность учащихся.
Описание места курса в учебном плане
В учебном плане школы отведено для данного курса 34 часа в 10 классе. Курс является развитием системы ранее приобретенных программных знаний.
Личностные, метапредметные и предметные результаты
освоения содержания курса
Программа позволяет добиваться следующих результатов освоения образовательной программы основного общего образования:
личностные:
ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
формирования коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой и других видах деятельности;
умения ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
первоначального представления о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичности мышления, умения распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативности мышления, инициативы, находчивости, активности при решении задач с параметрами;
умения контролировать процесс и результат учебной математической деятельности;
формирования способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
метапредметные:
способности самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умения осуществлять контроль по образцу и вносить необходимые коррективы;
способности адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
умения создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения задач с параметрами;
развития способности организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, взаимодействовать и находить общие способы работы; умения работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
развития способности видеть математическую задачу в других дисциплинах, в окружающей жизни;
умения находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умения выдвигать гипотезы при решении учебных задач и понимания необходимости их проверки;
понимания сущности алгоритмических предписаний и умения действовать в соответствии с предложенным алгоритмом;
умения самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
способности планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
предметные:
умения работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), развития способности обосновывать суждения, проводить классификацию;
владения базовым понятийным аппаратом: иметь представление о задачах с параметрами, аналитическим способом решения задач с параметрами(уравнений, неравенств и систем уравнений и неравенств), формирования представлений о графическом способе; координатная плоскость (х; а), координатная плоскость (а;х), координатная плоскость (х; у);
умения пользоваться изученными математическими формулами,"
знания основных способов представления и анализа статистических данных; умения решать задачи с помощью перебора всех возможных вариантов;
умения применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
ЗНАКОМСТВО С ПАРАМЕТРОМ.
Аналитический метод решения задач с параметрами.
Задачи, где параметр заменяется числом.
II. АНАЛИТИЧЕСКИЕ И ГРАФИЧЕСКИЕ ПРИЁМЫ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРАМИ.
.
1) Параметр и поиск решения уравнений, неравенств и их систем («ветвление»).
2) Параметр и количество решений уравнений, неравенств и их систем.
3) Параметр и свойства решения уравнений, неравенств и их систем.
4) Параметр как равноправная переменная.
5) Свойства функций в задачах с параметрами.
III. КВАДРАТИЧНАЯ ФУНКЦИЯ.
1)Дискриминант, старший коэффициент.
2)Вершина параболы.
3)Корни квадратичной функции.
Теорема Виета.
4)Расположение корней квадратичной функции относительно заданных точек.
5)Задачи, сводящиеся к исследованию расположения корней квадратичной функции.
Учебно-тематическое планирование.
| № урока | Тема урока | Кол-во часов | Дата по плану | Дата по факту |
| |||||
| | I ЗНАКОМСТВО С ПАРАМЕТРОМ. | 2
|
|
|
| |||||
| 11 | Аналитический метод решения задач с параметрами. | 1 |
|
|
| |||||
| 22 | Задачи, где параметр заменяется числом.
| 1 |
|
|
| |||||
|
| II АНАЛИТИЧЕСКИЕ И ГРАФИЧЕСКИЕ ПРИЁМЫ ЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРАМИ.
| 24 |
|
|
| |||||
| 3-4 | Параметр и поиск решения уравнений, неравенств и их систем | 2 |
|
|
| |||||
| 5-6 | Параметр и количество решений уравнений, неравенств и их систем | 2 |
|
|
| |||||
| 7-8 | Параметр и свойства решения уравнений, неравенств и их систем | 2 |
|
|
| |||||
|
|
|
| ||||||||
| 9-10 | Параметр как равноправная переменная | 2 |
|
|
| |||||
| 11-13 | Свойства функции в задачах с параметрами и модулями | 3 |
|
|
| |||||
| 14-16 | Графические приёмы. Координатные плоскости (х; а), (а;х) ,(х;у) | 3 |
|
|
| |||||
| 17-18 | Квадратичная функция | 2 |
|
|
| |||||
| 19-20 | Корни квадратичной функции | 2
|
|
|
| |||||
| 21-23 | Расположение корней квадратичной функции относительно заданных точек | 3 |
|
|
| |||||
| 24-26 | Задачи, сводящиеся к исследованию расположения корней квадратичной функции | 3 |
|
|
| |||||
|
| III. КВАДРАТИЧНАЯ ФУНКЦИЯ.
| 8 |
|
|
| |||||
| 27 | Дискриминант, старший коэффициент. | 1 |
|
|
| |||||
| 28 | Вершина параболы | 1 |
|
|
| |||||
| 29 | Корни квадратичной функции | 1 |
|
|
| |||||
| 30-31 | Расположение корней квадратичной функции относительно данной точки | 2 |
|
|
| |||||
| 32-33 | Решение заданий ЕГЭ | 2 |
|
|
| |||||
| 34 | Итоговое занятие | 1 |
|
|
| |||||
Перечень учебно-методического и материально-технического оснащение
Литература
Габович И.Г., Горнштейн П.И. Сколько корней имеет уравнение? // Квант. – 1985. - №3. – С. 43-46..
Говоров В.М., Дыбов П.Т., Мирошин Н.В., Смирнова С.Ф. Сборник конкурсных задач по математике (с методическими указаниями и решениями): Учебн. Пособие. – 2-ое изд. – М.: Наука, 1986. – 384 с.
Голубев В.И., Гольдман А.М., Дорофеев Г.В. О параметрах с самого начала // Репетитор. – 1991. - №2. – С. 3-13.
Горнштейн П.И., Полонский В.Б., Якир М.С. // Необходимые условия в задачах с параметрами // 1991. №11 С. 44-49.
Дорофеев Г.В. О задачах с параметрами, предлагаемых на вступительных экзаменах в вузы // Математика в школе. – 1983. - №4.– С. 36-40.
Марков В.К. Метод координат и задачи с параметрами. – М.: Изд-во Моск. ун-та, 1970. – 146с.
Пятьсот четырнадцать задач с параметрами // Под ред. Тынянкина С.А. – Волгоград 1991. – 160с.
Элективные курсы в профильном обучении. Образовательная область «Математика» /Министерство образования РФ – Национальный фонд подготовки кадров. – М. Вита – Пресс 2004. – 96с. – ISB №5-7755-0648-0.
Материально-техническое оснащение
Интерактивная доска
Мультимедийный проектор
Печатающее устройство
Интернет-источники:
www.ege.moipkro.ru
www.1september.ru
www.math.ru
www.allmath.ru
www.uztest.ru
http://schools.techno.ru/tech/index.html
http://www.catalog.alledu.ru/predmet/math/more2.html
http://195.19.32.10/physmath/index.ht
Проверочные (самостоятельные работы)
Задания для самостоятельной работы№1
Решить уравнения: Решить неравенства: При каких ![]()
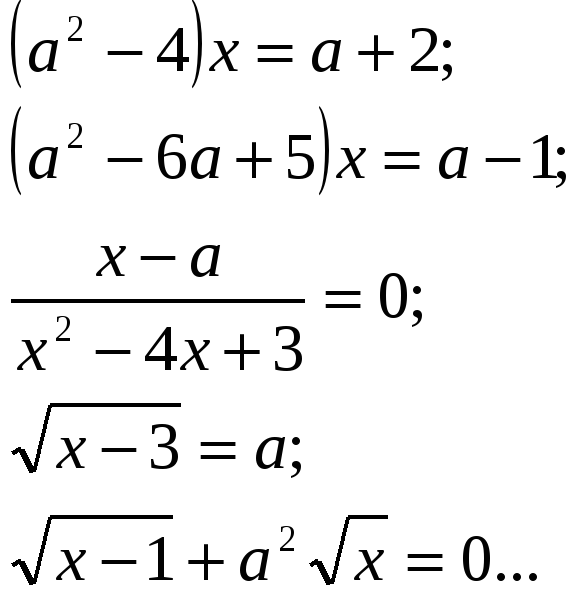 ;
; 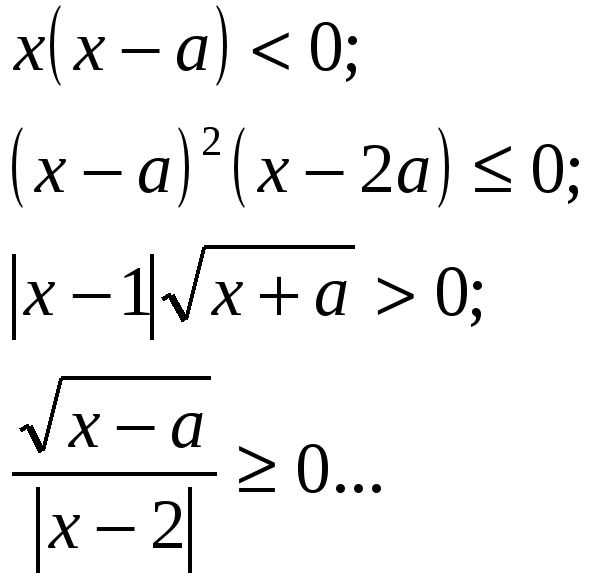 .
. 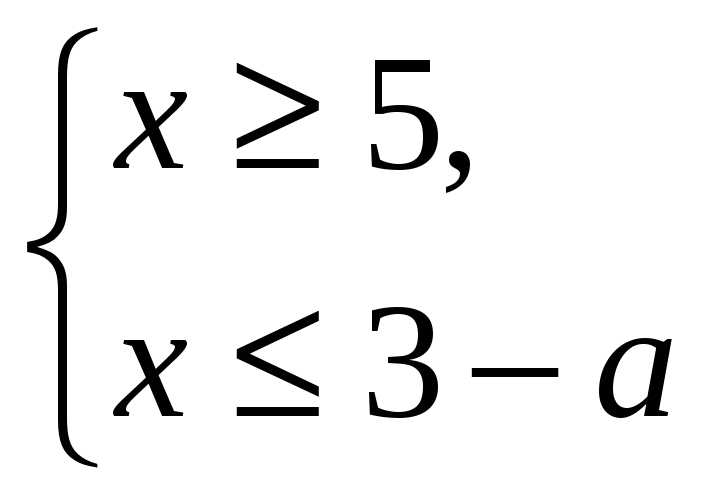 един. решение?
един. решение?
Задания для самостоятельной работы №2
Решить уравнение: Решить систему уравнений: Решить неравенства:
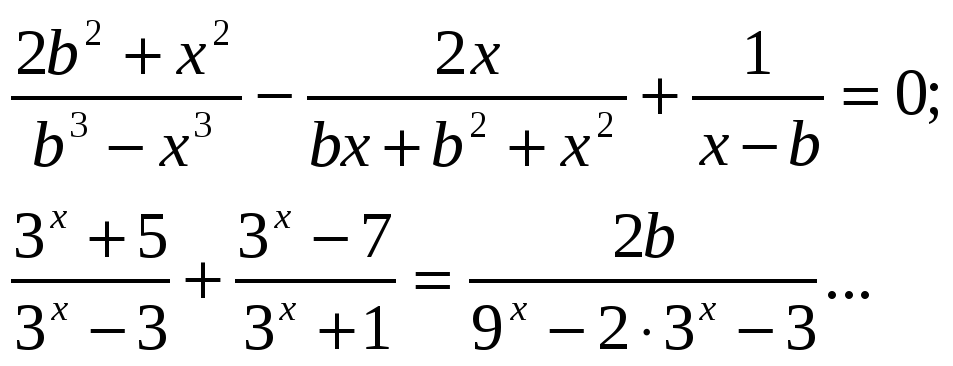
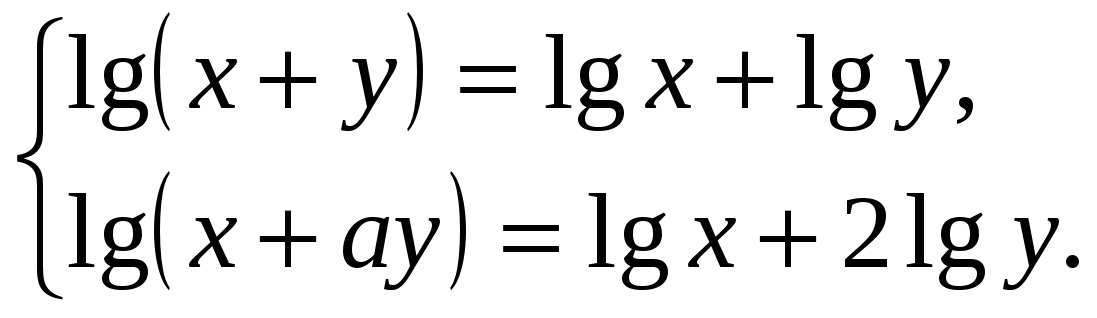
![]()
Задания для самостоятельной работы №3
Найти
 , при которых уравнение
, при которых уравнение 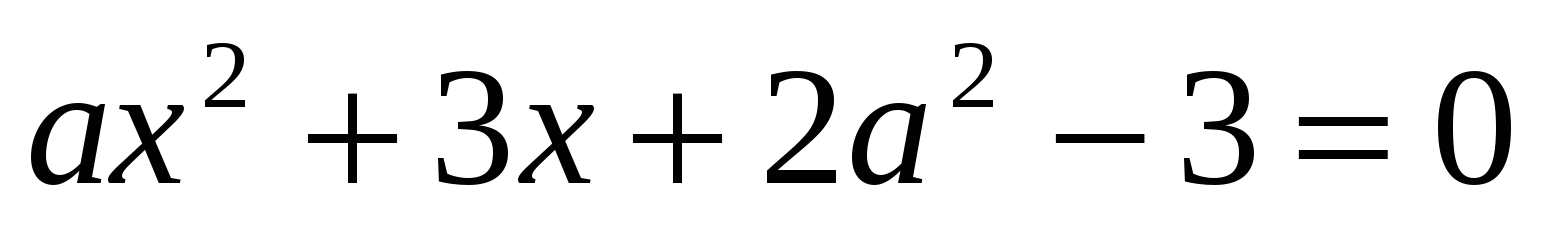 имеет только целые корни.
имеет только целые корни.В интервале (0;1) найти подмножество тех
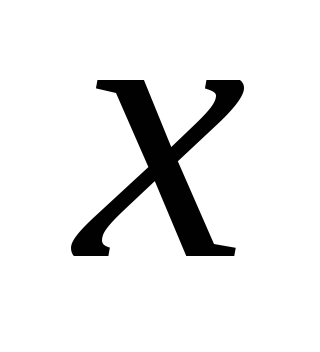 , для которых справедливо неравенство
, для которых справедливо неравенство 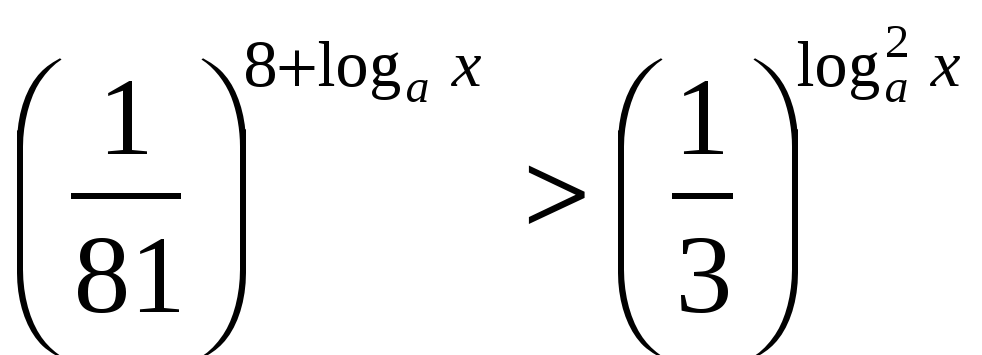 .
.
Найти все такие значения
 , при которых уравнения
, при которых уравнения 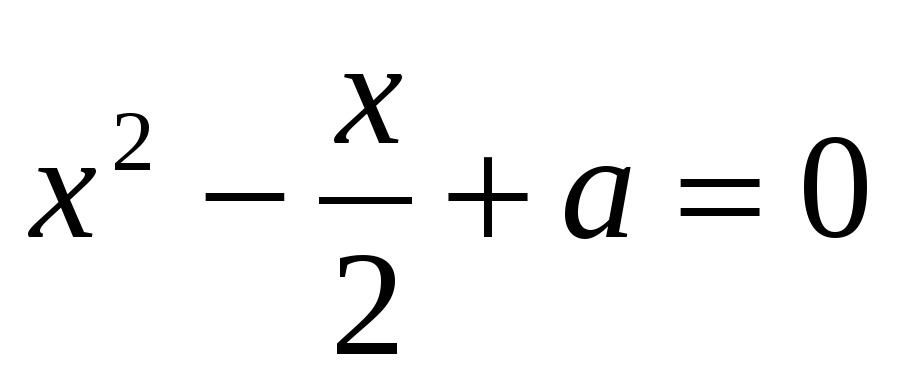 и
и 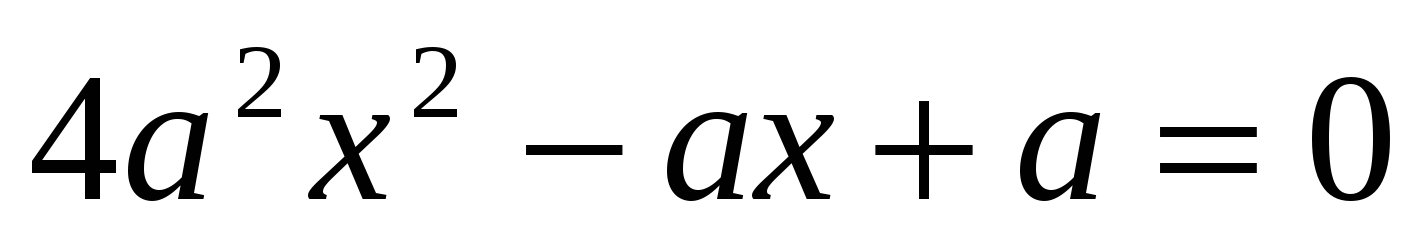 имеют общий действительный корень.
имеют общий действительный корень.Решить систему:
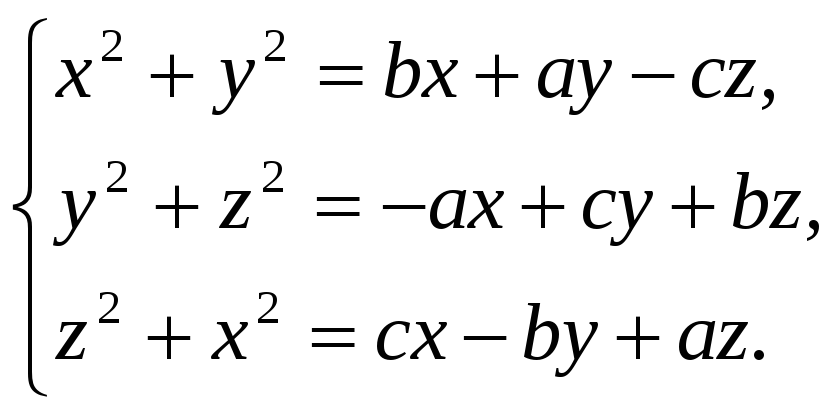
Задания для самостоятельной работы№4
Найти все положительные значения
 , при которых область значений функции
, при которых область значений функции 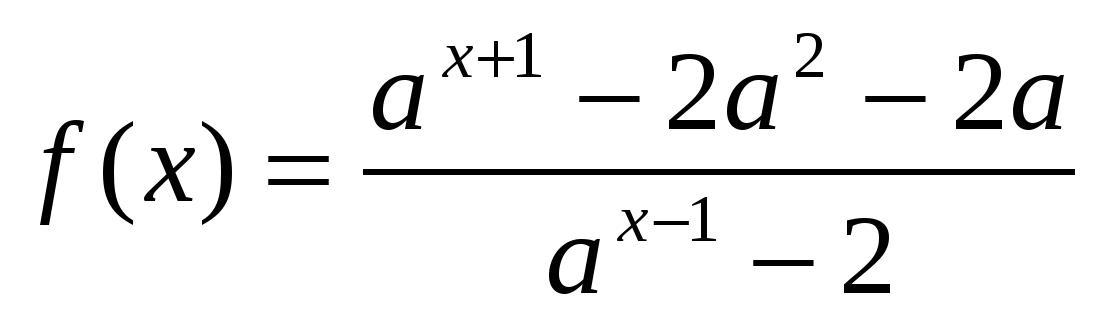 содержит все чётные целые числа.
содержит все чётные целые числа.Решить уравнение:
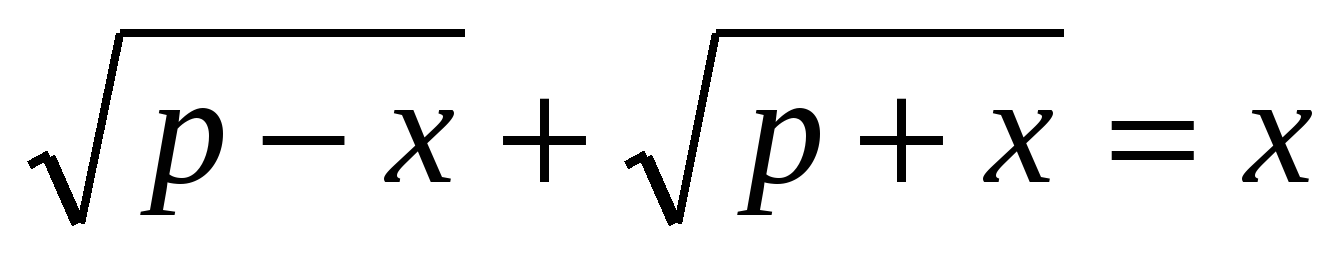 .
.
Найти все целые
 , при которых уравнение
, при которых уравнение 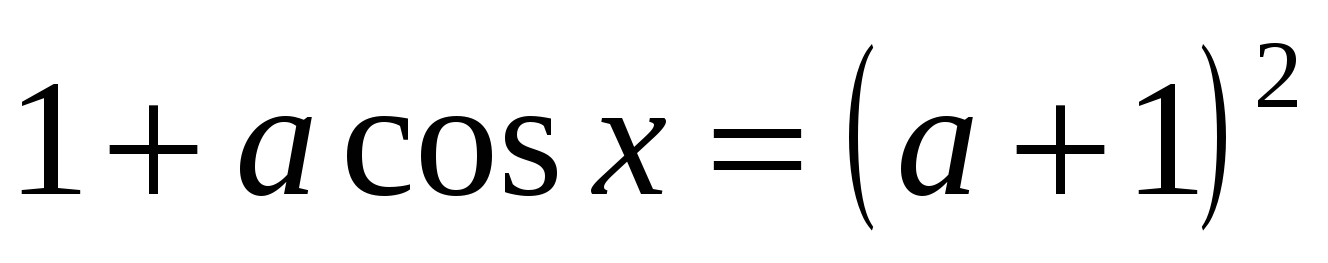 имеет решения.
имеет решения.Найти все значения
 , при каждом из которых выполняется неравенство
, при каждом из которых выполняется неравенство 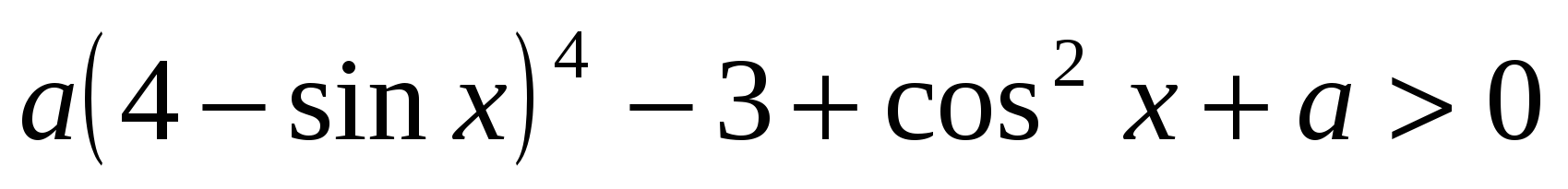 для всех
для всех 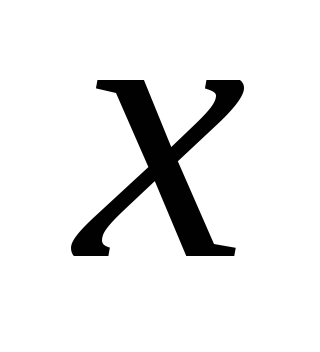 .
.
Задания для самостоятельной работы №5:
Для каждого значения параметра
 определить число решений уравнения
определить число решений уравнения 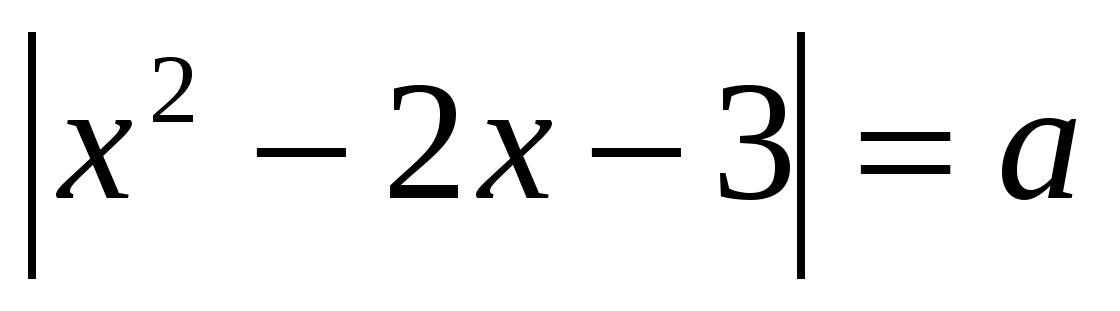 .
.Для каждого значения параметра
 решить неравенство .
решить неравенство .
При каких
 уравнение имеет три решения?
уравнение имеет три решения?При каких значениях параметра
 система уравнений имеет более двух различных решений?
система уравнений имеет более двух различных решений?
.
Задания для самостоятельной работы№6
Найти все значения параметра
 , при которых система неравенств удовлетворяет лишь при одном
, при которых система неравенств удовлетворяет лишь при одном  .
.
Найти все значения параметра
 , при каждом из которых уравнение имеет только один корень.
, при каждом из которых уравнение имеет только один корень.
Найдите все значения параметра
 , при которых система уравнений имеет решение.
, при которых система уравнений имеет решение.Найдите все значения
 , для которых неравенство выполняется при всех значениях
, для которых неравенство выполняется при всех значениях  .
.
Задания для самостоятельной работы №7
При каких значениях параметра
 наибольшее значение трёхчлена меньше четырёх?
наибольшее значение трёхчлена меньше четырёх?Найдите наибольшее и наименьшее значение функции на отрезке .
Пусть и - корни уравнения . Вычислите .
При каких значениях
 уравнение имеет два различных действительных корня и , удовлетворяющие неравенству ?
уравнение имеет два различных действительных корня и , удовлетворяющие неравенству ?
Итоговая работа
1. При каких значениях параметра ![]() уравнение имеет единственное решение?
уравнение имеет единственное решение?
2. Найти все такие значения параметра ![]() , при которых уравнение не имеет решений?
, при которых уравнение не имеет решений?
3. При каких значениях ![]() корни квадратного трёхчлена больше -2, но меньше 0?
корни квадратного трёхчлена больше -2, но меньше 0?
4. При каких ![]() система уравнений имеет хотя бы одно решение?
система уравнений имеет хотя бы одно решение?
5. Найдите все значения параметра ![]() , при каждом из которых неравенство выполняется для любого значения
, при каждом из которых неравенство выполняется для любого значения ![]() .
.
При каких значениях
 корни квадратного трёхчлена больше -2, но меньше 0?
корни квадратного трёхчлена больше -2, но меньше 0?
При каких
 система уравнений имеет хотя бы одно решение?
система уравнений имеет хотя бы одно решение?Найдите все значения параметра
 , при каждом из которых неравенство выполняется для любого значения
, при каждом из которых неравенство выполняется для любого значения  .
.
11

 Получите свидетельство
Получите свидетельство Вход
Вход












 Решение уравнений и неравенств с модулем и параметрами (220 KB)
Решение уравнений и неравенств с модулем и параметрами (220 KB)
 0
0 439
439 13
13 Нравится
0
Нравится
0


