
Урок алгебры
и начал анализа
в 11 класс
Учитель: Вязовченко Н.К.
г. Печоры, Псковская область
© Vyazovchenko N.K., 2009

Цели урока
- Познакомить учащихся с методами решения иррациональных неравенств

Проверка домашнего задания
Решение уравнения:

Устная работа с классом

- 2.Найдите область определения:
- 3.Объясните, почему эти уравнения не имеют решения на множестве действительных чисел.


Древнегреческий ученый-исследователь,
который впервые доказал существование иррациональных чисел
Ответьте на вопросы:
- 1. Что требуется для полученных значений переменной при решении иррациональных уравнений?
- 2. Способ, которым проводится проверка решений иррациональных уравнений.
- 3. Как называется знак корня?
- 4. Сколько решений имеет уравнение х 2 =а, если а
- 5. Как называются уравнения, в которых под знаком корня содержится переменная?
- 6. Как называется корень второй степени?
пров е рка
подстано в ка
ради к ал
но л ь
иррац и ональное
ква д ратный
 0? 5.Как называется корень уравнения, который получается в результате неравносильных преобразований? 6.Корень какой степени существует только из неотрицательного числа? " width="640"
0? 5.Как называется корень уравнения, который получается в результате неравносильных преобразований? 6.Корень какой степени существует только из неотрицательного числа? " width="640"
Кто впервые ввёл изображение корня?
о д но
н е чётной
к убический
дв а
посто р онний
чё т ной
Ответьте на вопросы:
1.Сколько решений имеет уравнение х 2 =0.
2.Корень какой степени существует из любого числа?
3.Как называется корень третей степени?
4.Сколько решений имеет уравнение х 2 =а, если а 0?
5.Как называется корень уравнения, который получается в результате неравносильных преобразований?
6.Корень какой степени существует только из неотрицательного числа?

Кто ввел современное изображение корня?
урав н ение
корен ь
трудол ю бие
прис т альный
равн о сильные
сопряже н ные
- урав н ение корен ь трудол ю бие прис т альный равн о сильные сопряже н ные
Ответьте на вопросы:
1.Как называется равенство двух алгебраических выражений?
2.Как называют значение переменной, при котором уравнение обращается в верное числовое равенство
3.Какая черта личности поможет при решении иррациональных уравнений?
4.Какой должен быть взгляд на уравнения, что бы не вычисляя сказать ответ?
5.Как называют уравнения, если они имеют одни и те же корни или не имеют корней вообще?
6.Как называется иррациональное выражение, содержащее противоположное арифметическое действие?

Решение иррациональных неравенств
- Неравенства, в которых неизвестная содержится под знаком радикала, называются иррациональными

Методы решения

- Если обе части неравенства возводятся в нечетную степень, то получаем равносильное неравенство.
- Если обе части неравенства возводятся в четную степень, то равносильное неравенство будем получать в том случае, если обе части неотрицательны .
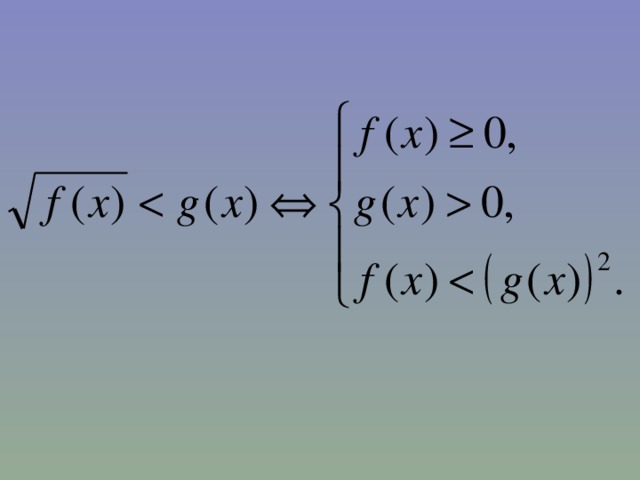
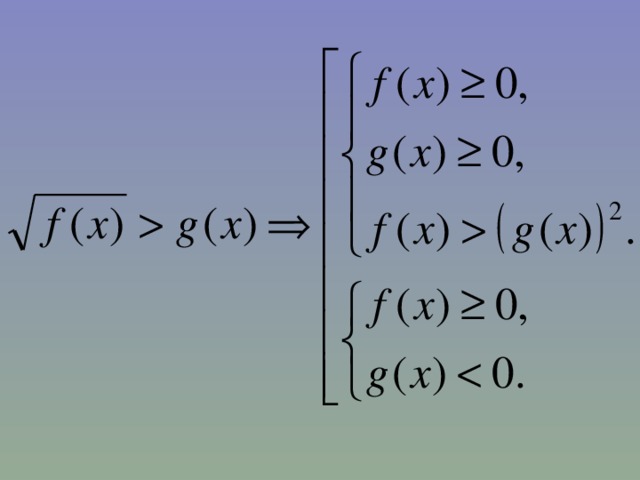

Решение примеров

Решение примеров
- Найти среднее арифметическое целых решений неравенства:

Решение примеров
- Для каждого действительного значения параметра а решить неравенство:

Домашнее задание
Решить неравенство:
1)
2)
3) Найдите наибольшее целое число, являющееся решением неравенства



 Получите свидетельство
Получите свидетельство Вход
Вход









 0? 5.Как называется корень уравнения, который получается в результате неравносильных преобразований? 6.Корень какой степени существует только из неотрицательного числа? " width="640"
0? 5.Как называется корень уравнения, который получается в результате неравносильных преобразований? 6.Корень какой степени существует только из неотрицательного числа? " width="640"




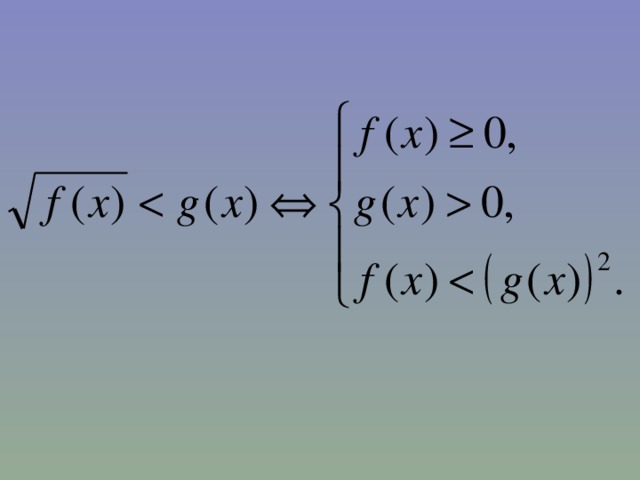
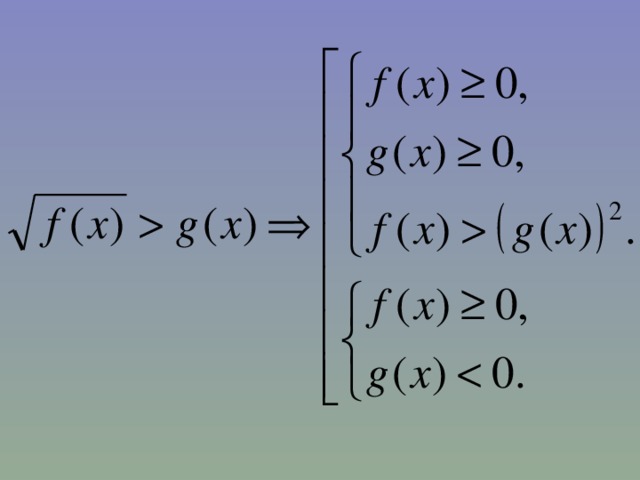














 Решение иррациональных неравенств (0.19 MB)
Решение иррациональных неравенств (0.19 MB)
 0
0 2028
2028 275
275 Нравится
0
Нравится
0




