Конспект урока по алгебре для учащихся 10 класса
Тема урока: «Иррациональные неравенства».
Цель урока:
образовательная: ввести понятие иррационального неравенства, научить решать простейшие иррациональные неравенства.
развивающая: развитие познавательного интереса учащихся; умения анализировать, сравнивать, сопоставлять; развитие наблюдательности, внимания; формировать потребность приобретения знаний; развитие математической речи учащихся.
воспитательная: формирование таких качеств личности, как организованность, ответственность, аккуратность, осознание общечеловеческих ценностей.
Учащиеся должны знать:
Определение иррационального неравенства
Учащиеся должны уметь:
Решать иррациональные неравенства
Тип урока: урок изучения нового материала
Методы обучения: индуктивно – репродуктивный
Формы работы: фронтальная, индивидуальная
Литература:
Алгебра и начала математического анализа. 10 класс: учеб. Для общеобразоват. Учреждений: базовый и профил. уровни/ [Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред. А. Б. Жижченко. –4–е изд. – М.: Просвещение, 2011. – 368с.
Алгебра и начала анализа. 10 класс : поурочные планы по учебнику Ш. А. Алимова и др. 1 полугодие / авт.–сост. Г. И. Григорьева. –Волгоград: Учитель, 2008. –150 с.
План урока
Организационный момент (1 минута)
Актуализация знаний и умений (5 минут)
Объяснение нового материала (20 минут)
Закрепление изученного материала (17 минут)
Подведение итогов (1 минута)
Домашнее задание (1 минута)
Ход урока:
Организационный момент
Включает в себя приветствие учителем учащихся, проверку отсутствующих, готовность помещения к уроку.
Деятельность учителя:
Запишите сегодняшнее число, классная работа и тему урока: «Иррациональные неравенства». Изучим понятие иррационального неравенства, разные методы решения иррациональных неравенств.
Запись на доске:
Число
Классная работа
Иррациональные неравенства
Актуализация знаний
| Деятельность учителя | Деятельность ученика | Запись на доске и в тетрадях |
| А сейчас давайте вспомним, какие уравнения называются иррациональными?
| В уравнениях, в которых неизвестная переменная х находится под знаком корня, называются иррациональными уравнениями.
|
|
| Какие из следующих уравнений являются иррациональными?
| Уравнения под пунктами а, в, г являются иррациональными уравнениями, так как неизвестные переменные находятся под знаком корня. | 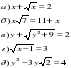
|
| Давайте вспомним, как решаются системы иррациональных уравнений |
| 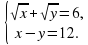
|
| Каким будет первое действие в нашем решении? Что мы находим в первую очередь? | Область допустимых значений: 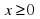 , ,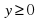 . .
| 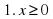 , ,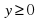 . .
|
| Так как и x, и y имеют положительные значения, то мы можем заменить выражение 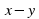 равносильным, но таким, чтобы первое и второе уравнение нашей системы перекликались. Итак, кто догадался, каким равносильным уравнением мы можем заменить выражение равносильным, но таким, чтобы первое и второе уравнение нашей системы перекликались. Итак, кто догадался, каким равносильным уравнением мы можем заменить выражение 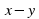 ? ? | Мы можем записать в виде разности квадратов корня их х и корня из у.
| 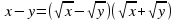
|
| Итак, наша система примет вид: |
| 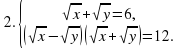
|
| Разделим второе уравнение системы на первое уравнение. |
| 3. 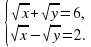 |
| Каким способом решим систему | Способом сложения | 4. 2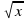 =8 =8 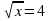
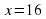
5.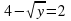 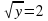
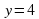
Ответ: (16;4) |
Объяснение нового материала
Деятельность учителя:
Иррациональные неравенства – это довольно сложный раздел школьного курса математики. Вы в начале урока сказали определение иррационального уравнения, а как вы думаете, каким будет определение иррационального неравенства.
Деятельность ученика:
Неравенства, содержащие неизвестное под знаком корня, называются иррациональными.
Деятельность учителя:
Рассмотрим задачу №1 на странице 199. Прочитайте текст задачи.
Деятельность ученика:
Стрельба из спортивного пистолета по круглой мишени диаметром 1м ведется из точки прямой, перпендикулярной плоскости мишени и проходящей через ее центр. На каком расстоянии от мишени должна быть точка выстрела, чтобы разность расстояний от нее до края мишени и до центра была не больше 2 см?
Деятельность учителя:
Изучите рисунок 82.
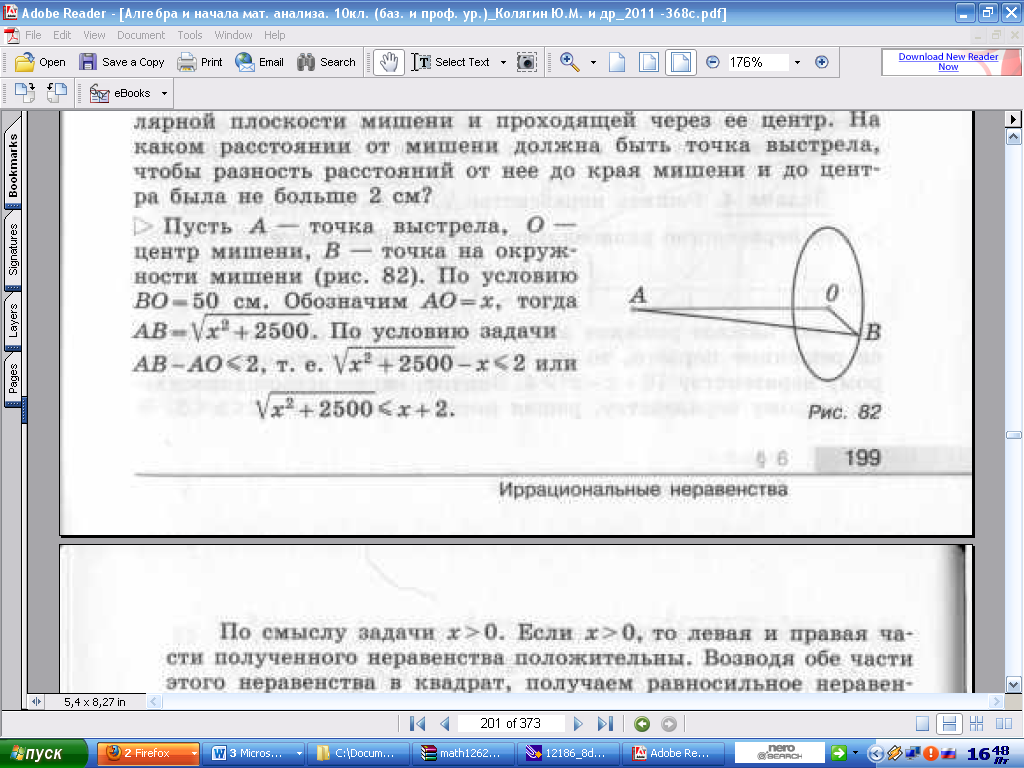
Точку А обозначили за точку выстрела, точка О – центр мишени, В – точка на окружности мишени. Что известно нам из условия задачи?
Запись на доске и в тетрадях:
А – точка выстрела;
О – центр мишени;
В – точка на окружности мишени.
Деятельность ученика:
Диаметр мишени равен 1м.
Деятельность учителя:
Можем тогда найти радиус мишени
Деятельность ученика:
Отсюда радиус мишени равен 50 см.
Запись на доске и в тетрадях:
ВО – радиус мишени;
ВО=50(см).
Деятельность учителя:
Что необходимо найти в этой задаче?
Деятельность ученика:
Расстояние от точки выстрела до мишени.
Деятельность учителя:
Тогда из рисунка, какой отрезок мы обозначим за неизвестное?
Деятельность ученика:
АО – расстояние от точки выстрела до мишени
АО обозначим за х
Запись на доске и в тетрадях:
АО – расстояние от точки выстрела до мишени
АО=х
Деятельность учителя:
А какое важное условие нам известно из задачи?
Деятельность ученика:
Разность расстояний от точки выстрела до края мишени и до центра должна быть не больше 2 см.
Деятельность учителя:
Тогда мы можем составить неравенство:
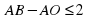 (1)
(1)
Осталось найти значения АВ и АО
Рассмотрим прямоугольный треугольник АОВ, где АВ –гипотенуза. Найдем АВ по теореме Пифагора.
Запись на доске и в тетрадях:
АВ=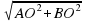
Деятельность учителя:
ВО нам известно, получим:
Запись на доске и в тетрадях:
АВ=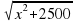
Деятельность учителя:
Теперь АВ и АО нам известны, подставляем в наше неравенство(1), получим:
Запись на доске и в тетрадях:
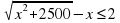
Деятельность учителя:
Мы получили иррациональное уравнение. Из этой задачи видите, что многие задачи мы сможем решать с помощью иррациональных неравенств. А теперь решим это иррациональное неравенство. Для удобства решения перенесём x в правую часть неравенства.
Запись на доске и в тетрадях:
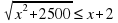
Деятельность учителя:
Так как мы ищем расстояние, а расстояние не может быть отрицательным числом, то у нас x принимает только положительные значения. Тогда мы можем возвести обе части нашего неравенства в квадрат, получим:
Запись на доске и в тетрадях:
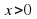
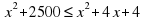
Деятельность учителя:
С неизвестными перенесем вправо, а с известными влево. Получим:
Запись на доске и в тетрадях




Деятельность учителя:
То есть, расстояние от точки выстрела до мишени должно быть не меньше 624. Итак, в дальнейшем вам будут встречаться задачи, при решении которых вам необходимо будет прибегать к составлению иррациональных неравенств.
Основным методом решения иррациональных неравенств является сведение неравенства к равносильной системе или совокупности систем рациональных неравенств:
1)Неравенство  равносильно системе
равносильно системе
2)Неравенство  равносильно совокупности систем и
равносильно совокупности систем и
При решении нашего неравенства мы воспользовались одним из методов решения иррациональных неравенств, это возведение обеих частей неравенства в одну и ту же натуральную степень, существуют и другие методы решения, такие, как:
С ними мы познакомимся чуть позже.
Для решения иррациональных неравенств вам необходимо запомнить следующие правила:
1. при возведении обеих частей неравенства в нечётную степень всегда получается неравенство, равносильное данному неравенству;
2. если обе части неравенства возводят в чётную степень, то получится неравенство, равносильное исходному только в том случае, если обе части исходного неравенства неотрицательны.
Закрепление изученного материала
Деятельность учителя:
Начнем решать простейшие иррациональные неравенства и постепенно перейдем к решению более сложных.
Давайте решим устно задачу 5 под пунктом 1на странице 201.

Определим область допустимых значений в левой части
Деятельность ученика:
Левая часть всегда положительна
Деятельность учителя:
А какое число в правой части?
Деятельность ученика:
В правой части отрицательное число
Деятельность учителя:
Как думаете, каким будет решение этого иррационального неравенства?
Деятельность ученика:
Так как правая часть всегда положительна, а в левой части отрицательное число, то это неравенство не имеет решения.
Деятельность учителя:
А теперь давайте рассмотрим задачу 2. К доске пойдет…(К доске выходит ученик)
Что от нас требуется.
Деятельность ученика:
Решить неравенство.
Запись на доске и в тетрадях:

Деятельность учителя:
В правой части положительное число, а какие значения принимает левая часть?
Деятельность ученика:
Левая часть неравенства принимает только положительные значения
Деятельность учителя:
Воспользуемся готовыми формулами для перехода от неравенства к равносильной системе неравенств.
Запись на доске и в тетрадях:
Деятельность учителя:
Данная система будет равносильна системе:
Деятельность ученика:

Запись на доске и в тетрадях:


Деятельность учителя:
Запишите ответ в виде двойного неравенства
Запись на доске и в тетрадях:
Ответ: 
Деятельность учителя:
А теперь самостоятельно попробуйте решить неравенство такого вида  , а один ученик решит сзади доски, затем сравним результаты.(все решают у себя в тетрадях, а один ученик вызывается к доске)
, а один ученик решит сзади доски, затем сравним результаты.(все решают у себя в тетрадях, а один ученик вызывается к доске)
Запись на доске и в тетрадях:




+
+
–


 x1=3
x1=3
3
-2
x2=-2
Ответ: -2
Подведение итогов
Деятельность учителя:
Какие неравенства мы решали на уроке?
Деятельность ученика:
На уроке мы решали иррациональные неравенства.
Деятельность учителя:
Дайте определение иррационального неравенства.
Деятельность ученика:
Неравенства, содержащие неизвестное под знаком корня, называются иррациональными.
Деятельность учителя:
Каким методом решали иррациональные неравенства?
Деятельность ученика:
Возведением обеих частей неравенства в одну и ту же натуральную степень;
Домашнее задание
Деятельность учителя: Рассмотреть задачу 6. Решить 76(4,6);77(2,4).

 Получите свидетельство
Получите свидетельство Вход
Вход



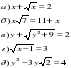
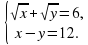
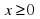 ,
,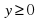 .
.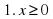 ,
,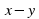 равносильным, но таким, чтобы первое и второе уравнение нашей системы перекликались. Итак, кто догадался, каким равносильным уравнением мы можем заменить выражение
равносильным, но таким, чтобы первое и второе уравнение нашей системы перекликались. Итак, кто догадался, каким равносильным уравнением мы можем заменить выражение 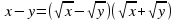
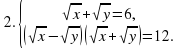
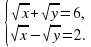
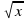 =8
=8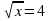
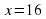
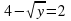
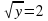
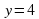

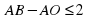 (1)
(1)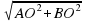
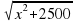
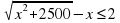
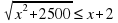
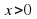
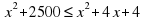









 Конспект урока по алгебре и началам анализа "Иррациональные неравенства" (0.39 MB)
Конспект урока по алгебре и началам анализа "Иррациональные неравенства" (0.39 MB)
 0
0 3326
3326 806
806 Нравится
0
Нравится
0


