Рекурсия

Рекурсивным называется объект, который частично определяется через самого себя. То есть рекурсивными называются подпрограммы (процедуры и функции), которые вызывают сами себя. Идеи рекурсии известны людям издавна. Рекурсивные определения как мощный аналитический аппарат используются во многих областях науки, особенно в математике. Рассмотрим функцию факториала n!. Как правило, ее определяют как произведение первых n целых чисел.

Такое произведение конечно можно легко вычислить с помощью итеративных конструкций, например, оператора цикла for.

program Factorial ;

var

Fact : Longint ;

n, i : Integer;

begin

Write  ('Введите число  n: ');

Readln ( n ) ;

Fact := 1;

for i := 1 to n do Pact := Fact * i;

Writeln ('Факториал  n! = ', Fact);

end.

Однако существует также другое определение факториала, в котором используется рекуррентная формула и которое имеет такой вид:
(1) 0! = 1
(2) для всех n > 0 n! = n * (n-1)!
 Определения с помощью рекуррентных формул иногда называют рекурсивными определениями.

Понятно, что организовать вычисления по рекуррентным формулам можно и без использования рекурсии. Однако при этом встает вопрос о качестве программы, и доказательстве ее эквивалентности начальным формулам. Использование рекурсии позволяет легко (почти дословно) запрограммировать вычисления по рекуррентным формулам.

Содержание и мощность рекурсивного определения, а также его главное назначение, состоит в том, что оно позволяет с помощью конечного выражения определить бесконечное множество объектов. Аналогично с помощью конечного рекурсивного алгоритма можно, определить бесконечное вычисление, причем алгоритм не будет содержать повторений фрагментов текста.
Для создания рекурсивных алгоритмов необходимо и достаточно наличие понятия процедуры или функции. Это вытекает из того, что процедуры и функции позволяют дать любой последовательности действий (операторов) имя, с помощью которого можно будет эту последовательность действий вызывать.

Р Е К У Р С И Я  

Волков А.А.

2

Рекурсивным называется объект, который частично определяется через самого себя. То есть рекурсивными называются подпрограммы (процедуры и функции), которые вызывают сами себя. Идеи рекурсии известны людям издавна. Рекурсивные определения как мощный аналитический аппарат используются во многих областях науки, особенно в математике. Рассмотрим функцию факториала n!. Как правило, ее определяют как произведение первых n целых чисел.

3

Такое произведение конечно можно легко вычислить с помощью итеративных конструкций, например, оператора цикла for .

program Factorial ;

var

Fact : Longint ;

n, i : Integer;

begin

Write (' Введите число n: ');

Readln ( n ) ;

Fact := 1;

for i := 1 to n do Pact := Fact * i;

Writeln (' Факториал n! = ', Fact);

end .

0 n! = n * (n-1)!   Определения с помощью рекуррентных формул иногда называют рекурсивными определениями. " width="640"

4

Однако существует также другое определение факториала, в котором используется рекуррентная формула и которое имеет такой вид: (1) 0! = 1 (2) для всех n 0 n! = n * (n-1)!   Определения с помощью рекуррентных формул иногда называют рекурсивными определениями.

5

Понятно, что организовать вычисления по рекуррентным формулам можно и без использования рекурсии. Однако при этом встает вопрос о качестве программы, и доказательстве ее эквивалентности начальным формулам. Использование рекурсии позволяет легко (почти дословно) запрограммировать вычисления по рекуррентным формулам.

6

Содержание и мощность рекурсивного определения, а также его главное назначение, состоит в том, что оно позволяет с помощью конечного выражения определить бесконечное множество объектов. Аналогично с помощью конечного рекурсивного алгоритма можно, определить бесконечное вычисление, причем алгоритм не будет содержать повторений фрагментов текста.

7

Для создания рекурсивных алгоритмов необходимо и достаточно наличие понятия процедуры или функции. Это вытекает из того, что процедуры и функции позволяют дать любой последовательности действий (операторов) имя, с помощью которого можно будет эту последовательность действий вызывать.

8

Например, следующая процедура будет бесконечно печатать известные всем строки. Program EndLess 1 ; procedure PopeAndDog 1 ; begin WriteIn('У попа была собака, он ее любил.'); WriteIn ('Она съела кусок мяса, он ее убил,'); WriteIn ('похоронил и надпись написал:') ; PopeAndDog 1 end; begin PopeAndDog 1 end.

9

В действительности при исполнении на компьютере такой бесконечный вызов приводит к переполнению стека и возникновению ошибки времени исполнения. Программы, в которых используются рекурсивные процедуры отличаются простотой, наглядностью и компактностью текста.

10

Такие качества рекурсивных алгоритмов вытекают из того, что рекурсивная процедура указывает что нужно делать, а нерекурсивная больше акцентирует внимание на том, как нужно делать. Однако за эту простоту приходится расплачиваться неэкономным пользованием оперативной памяти, так как выполнение рекурсивных процедур требует значительно большего размера оперативной памяти во время выполнения, чем нерекурсивных. При каждом рекурсивном вызове для локальных переменных, а также для параметров процедуры, выделяются новые ячейки памяти.

11

В общем случае любая рекурсивная процедура Rec включает в себя некоторое множество операторов S и один или несколько операторов рекурсивного вызова Р. Как было показано выше, безусловные рекурсивные процедуры приводят к бесконечным процессам, и на эту проблему нужно обратить особое внимание, так как практическое использование процедур с бесконечным самовызовом невозможно. Такая невозможность вытекает из того, что для каждой копии рекурсивной процедуры необходимо выделять дополнительную область памяти, а бесконечной памяти не существует.

12

Следовательно, главное требование к рекурсивным процедурам заключается в том, что вызов рекурсивной процедуры должен выполняться по условию, которое на каком-то уровне рекурсии станет ложным.

13

Если условие истинно, то рекурсивный спуск продолжается. Когда оно становится ложным, то спуск заканчивается и начинается поочередный рекурсивный возврат из всех вызванных на данный момент копий рекурсивной процедуры. Структура рекурсивной процедуры может принимать три разных формы:

14

1. Форма с выполнением действий до рекурсивного вызова (с выполнением действии на рекурсивном спуске). procedure Rec; begin, S; if условие then Rec; end ;

15

2. Форма с выполнением действий после рекурсивного вызова (с. выполнением действий на рекурсивном возврате). procedure Rec; begin if условие then Rec; S ; end ;

16

3. Форма с выполнением действий как до, так и после рекурсивного вызова (с выполнением действий как на рекурсивном спуске, так и на рекурсивно возврате).

procedure Rec;

begin

if условие then

begin

S 1 ;

Rec;

S2;

End;

procedure Rec; begin S 1 ; if условие then Rec; S2; end;

17

Первые две формы рекурсивных подпрограмм рассмотрим на примере вычисления факториала ( n !), третью форму — на примере реверсивной печати вводимой строки.

18

Для реализации универсального алгоритма вычисления факториала, работающего на спуске, в рекурсивную функцию требуется дополнительно ввести два параметра: Mult — для выполнения до рекурсивного вызова (то есть на спуске) операции умножения накапливаемого значения факториала на очередной множитель; m — для обеспечения независимости рекурсивной функции от имени конкретной глобальной переменной, то есть для повышения универсальности функции.

1 9

Program Factorial_Down ; Var n : Integer; function Fact_Dn(Mult:Longint; i, m : Integer ): Longint; begin Mult := Mult * i ; { Накопление факториала стоит до оператора рекурсивного вызова. Следовательно вычисление выполняется на спуске . } if i=m then Fact Dn := Mult else Fact Dn := Fact Dn ( Mult, i+1, m ) end; Writeln (' Введите число n: ') ; readln ( n ) ; Writeln(' Факториал n! = ', Fac_ Dn ( 1, 1, n )); end . .  

20

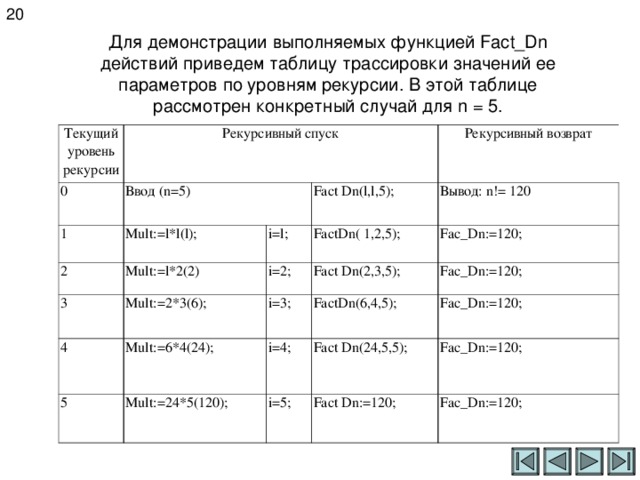
Для демонстрации выполняемых функцией Fact _ Dn действий приведем таблицу трассировки значений ее параметров по уровням рекурсии. В этой таблице рассмотрен конкретный случай для n = 5.

Текущий уровень

рекурсии

Рекурсивный спуск

0

1

Ввод ( n =5)

Mult:=l*l(l);

2

3

i=l;

Mult:=l*2(2)

Рекурсивный возврат

Fact Dn(l,l,5);

Mult:=2*3(6);

FactDn( 1,2,5);

Вывод: n != 120

4

i=2;

5

Mult:=6*4(24);

i=3;

Fact Dn(2,3,5);

Fac_D n:=120 ;

FactDn(6,4,5);

Mult:=24*5(120);

Fac_D n:=120 ;

i=4;

Fac_D n:=120 ;

Fact Dn(24,5,5);

i=5;

Fact Dn:=120;

Fac_D n:=120 ;

Fac_D n:=120 ;

21

Для демонстрации работы на рекурсивном возврате, приведем программу Factorial _ Up , использующую функцию Fact _ Up , в которой рекурсивный вы­зов и оператор накопления факториала разделены явным образом.

22

program Factorial Up; var n : Integer; function Fact_Up (i : Integer ): Longint; var Mult : Longint; begin if i = 1 then Mult:=1 else Mult:=Fact_Up ( i-1 ) ; Fact Up := Mult * i { Накопление факториала стоит после } { оператора рекурсивного вызова. } { Следовательно вычисление выполняется } {на возврате. } end ; begin Write ('Введите число n :'); Readln ( n ) ; Writeln (' Факториал n! =', Fact _ Up ( n )) ; end.

23

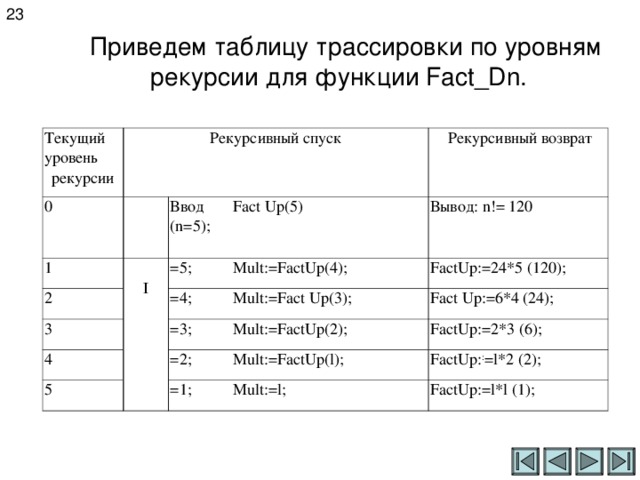
Приведем таблицу трассировки по уровням рекурсии для функции Fact _ Dn .

Текущий уровень

рекурсии

Рекурсивный спуск

0

1

I

Ввод ( n =5);

2

Рекурсивный возврат

Fact Up(5)

=5;

3

Mult:=FactUp(4);

4

=4;

Вывод: n != 120

=3;

5

FactUp:=24*5 (120);

Mult:=Fact Up(3);

Mult:=FactUp(2);

Fact Up:=6*4 (24);

=2;

FactUp:=2*3 (6);

Mult:=FactUp(l);

=1 ;

Mult:=l;

FactUp: : =l*2 (2);

FactUp:=l*l (1);

24

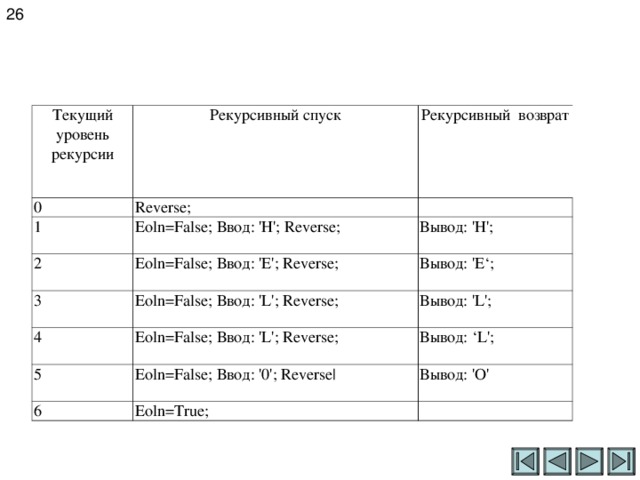
Третью форму рекурсивных подпрограмм покажем на примере следующей задачи. Задача: Вывести на печать символы введенной строки ' HELLO ' в обратном направлении. Решение этой задачи выполнено в виде показанной ниже программы Reverse _ String , использующей рекурсивную процедуру Reverse . Напомним, что функция eoln возвращает значение, равное False , если c трока еще не окончилась, и значение, равное True , когда считывается последний символ строки.

25

program Reverse_String; procedure Reversse ; var Ch : Char; begin if not eoln then begin Read ( Ch ) ; Reverse ; Write ( Ch ) ; end end; begin Reverse end.

26

Текущий уровень рекурсии

Рекурсивный спуск

0

1

Reverse;

Рекурсивный возврат

Ео ln=False; Ввод : ' Н '; Reverse;

2

Вывод: 'Н';

Ео ln=False; Ввод : ' Е' ; Reverse;

3

Ео ln=False; Ввод : ' L'; Reverse;

Вывод: 'Е‘;

4

Вывод: ' L ';

5

Ео ln=False; Ввод : 'L ' ; Reverse;

Ео ln=False; Ввод : '0'; Reverse|

6

Вывод: ‘ L ';

Вывод: ' O '

Ео ln =Т rue ;

27

Заключение

Все формы рекурсивных процедур находят применение на практике. Многие задачи, в том числе вычисление факториала, безразличны к тому, какая используется форма рекурсивной процедуры.

Однако есть классы задач, при решении которых программисту требуется сознательно управлять ходом работы рекурсивных процедур и функций.

28

Спасибо за внимание!

1

2

3

4

5

6

7

8

9

10

1 7

2 0

1 9

1 8

1 3

1 6

1 5

1 4

1 2

1 1

21

22

23

24

25

26

27