Развитие навыков исследовательской работы учащихся при решении задач с параметрами

Развитие навыков исследовательской работы

учащихся при решении задач с параметрами

Параметр ( греческое - parametron –измеряющий) в математике это величина, числовое значение которой постоянно сохраняется на протяжении всего решения данной задачи.

Параметр имеет двоякую природу: с ним «общаются» как с числом, однако степень «общения» ограничивается тем, что он все-таки неизвестная величина. При решении задач с параметрами нужно быть предельно внимательным.

Задачи с параметрами дают большие возможности для полноценной математической деятельности учащихся, открывают им значительное количество эвристических приемов общего характера, важных для математического развития личности, что используется в исследованиях на другом учебном материале. Наблюдая за тем, как ученик решает задачи с параметрами, можно проверить уровень его логического мышления, начальные навыки исследовательской деятельности.

Аналитические и графические приемы решения задач с параметрами

В дальнейшем будем иметь в виду, что знакомство с отдельными задачами – это знакомство с методами решения целого класса задач.

Задачи, в которых требуется, чтобы ответ удовлетворял некоторые условия относительно значений параметра

Эти задачи формулируются так: при каких значениях параметра уравнение ( неравенство, система) имеют определенное количество решений или решения, большие ( меньшие) заданного числа; или находятся на данном отрезке и др.

Такие задачи решаются аналитически, графически или объединением этих методов. Рассмотрим отдельные задачи и попробуем составить общие схемы решения.

Задание № 1. При каких значениях параметра а уравнение 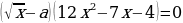имеет одно решение?

Решение 1. Уравнение данного типа имеет решение, если хотя бы один множитель равен нулю, а другие при этом не теряют смысла

2. Множитель 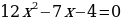имеет два корня 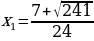; независимо от значений параметра а. Множитель 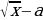имеет корень 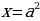, при этом если а меньше нуля - решений нет, при .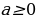

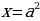3.Проведем анализ. При 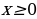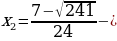меньше нуля- не удовлетворяет условию .Для обеспечения выполнения условия по поводу количества корней будем требовать, чтобы корн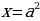и и 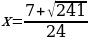совпадали: ; .

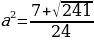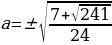Ответ: .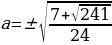

Задание № 2 Найти все решения неравенства 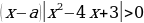в зависимости от параметра а.

Решение 1. Анализ. Множитель 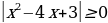всегда , так как 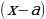вынужден быть положительным. Получим систему

2. Наносим решение каждого неравенства на две числовые прямые:

3.Первое решение не зависит от а. Мысленно будем двигать начало из а луча, рассматривая все возможные случаи и с полученных рисунков списывать ответ.

Задание № 3 При каких значениях параметра а уравнение

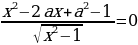
не имеет решений ( имеет одно решение ).

Задачи этого типа лучше решать по такой схеме.

Решение 1. Область определения уравнения: 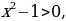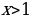, х -1.

2.Ошибочно думать, что дискриминант числителя меньше нуля и только . Он может быть неотрицательным, но найденные корни не должны удовлетворять ОДЗ.

3. Найдем дискриминант числителя 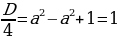,тогда корни всегда разные ,

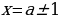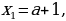
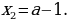
4.Обязанность параметра – обеспечить, чтобы 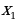и 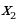не попали в ОДЗ. Находим для этого необходимые и достаточные условия: .

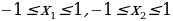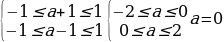
Ответ : а = 0.

Параметр как равноправная переменная

С формальной точки зрения параметр такая же переменная, как и другие переменные в задачах . Этим можно воспользоваться при решении уравнений и неравенств, решать задачи относительно параметра, считая основную переменную параметром.

Указания для применения метода решения относительно параметра

1. Этот метод целесообразно использовать, когда выражение имеет высокую степень относительно переменной и одновременно является линейным или квадратным относительно параметра.

2. Если условие задачи подсказывает, что переменную по смыслу задачи выгодно считать параметром, а параметр считать переменной.

3. Если ГМТ, заданное в условии уравнением или неравенством, удается изобразить на координатной плоскости «переменная – параметр».

Задание № 4. Найти все значения х, которые удовлетворяют неравенству

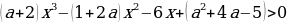хотя бы при одном значении а из отрезка .

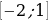Решение 1 .Перепишем неравенство по степеням а:

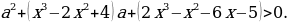
2.Переформулируем задачу: найти необходимые и достаточные условия, при которых квадратный трехчлен 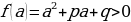хотя бы в одной точке отрезка .

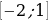3. Рисунок и запись достаточных условий: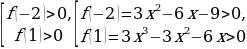

Ответ: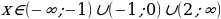

Задачи со свободным параметром

В условии некоторых задач одному из параметров или переменной разрешается принимать произвольные значения из некоторого множества ( свободный параметр, переменная).При этом необходимо найти такие значения другого параметра, при которых выполняются определенные условия.

Схема решения таких задач

1.Придают свободному параметру некоторые значения с целью упростить выражение, после чего находят необходимые условия для искомого ( другого ) параметра.

2.Подстановкой найденных значений искомого параметра и проверкой выполнения заданных условий изучают достаточность полученных значений.

Задание № 5 Найти все значения а, при которых система

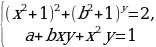
имеет хотя бы одно решение для произвольных значений b.

Решение Система должна иметь решение при произвольном значении b, в частности, при b=0 ( при 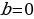система приобретает особо простой вид). .

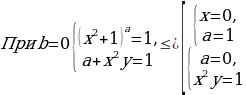Для выполнения условий задачи необходимо а=0 или а = 1. Другие значения можно не исследовать.

Достаточность .1 .При а=0 система имеет вид:

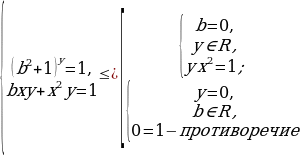
При не равном нулю система решений не имеет.

2.При а=1 система принимает вид:

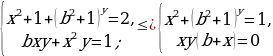
Пара 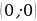– решение последней системы для всех .

Ответ: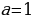

Графический способ решения задач с параметрами

Графики уравнений выполняют важную роль при решении задач с параметрами. Они позволяют представить все возможные варианты взаимного расположения множества точек и найти для этого достаточные условия.

При этом важно, чтобы учащиеся хорошо понимали, что функция с параметром – это целая совокупность графиков 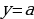–совокупность прямых, параллельных оси Ох; 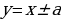– совокупность прямых, параллельных биссектрисе у=х; 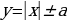– совокупность углов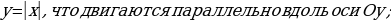 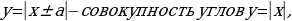которые двигаются параллельно вдоль оси Ох; 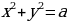-окружность, которая увеличивается, если 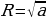увеличивается.

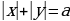- гомотетия с центром (0;0);

у=ах –поворот прямой около центра О (0;0).

Задачи на нахождение числа решений уравнения в зависимости от параметра

Задача № 6 Для каждого значения параметра а найти число решений уравнения

.

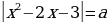Решение 1. Перенести в одну часть члены с неизвестными, а в другую с параметром.

2. Обозначить левую и правую части уравнения как функции.

3.Построить график той функции, которая не зависит от параметра.

4. Применить пересечение графика пучком параллельных прямых.

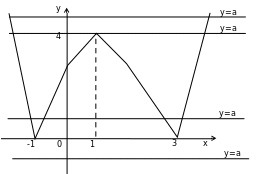5.С рисунка списать ответ.

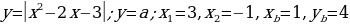
Ответ: ;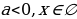

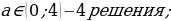
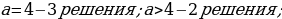
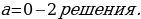
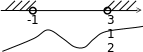
Задание № 7. При каких значениях а решением системы неравенств

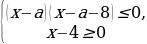
является отрезок, длина которого равна 5?

Решение 1. Решить то неравенство, которое не зависит от параметра.

2.Решить неравенство с параметром.

3.Найти пересечение решений и учесть условие, что указанное пересечение должно удовлетворять данное в задаче условие: 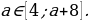Расстояние между точками 4 и а+ 8 должно равняться 5.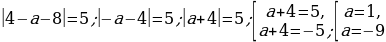

При проверке убеждаемся , что а = -9 – посторонний корень.

Ответ: а=1.

Рассмотренные задачи с параметрами представляют далеко не все классы задач, которые должны уметь решать ученики старших классов с углубленным изучением математики.