Разработка урока по теме "Множества"

А--11

Урок №

Множество и его элементы. Пустое множество.

Способы задания множеств. Подмножества данного множества.

Операции над множествами.

Цель урока: Формировать знания учащихся о множествах и его элементах,

пустом множестве, способах задания множеств, операциях над

множествами: объединение, пересечение, разность.

Ход урока:

Восприятие нового материала:

МНОЖЕСТВО — одно из основных понятий математики, которое не подлежит формальному определению. МНОЖЕСТВО --- можно представить как совокупность некоторых предметов, объединенных по определенному характеристическому признаку.

Например:1). Множество цифр: 0;1;2;3;4;5;6;7;8;9.

2). Множество букв русского алфавита.

Предметы, из которых состоит множество, называются его ЭЛЕМЕНТАМИ.

Например:1).цифра 6 – элемент множества цифр.

2). Буква Р – элемент множества букв русского алфавита.

Для обозначения множеств используют большие буквы латинского алфавита или фигурные скобки, внутри которых записывают элементы множества(при этом порядок элементов не имеет значения).

Например:1). А— множество цифр: А={0;1;2;3;4;5;6;7;8;9}.

2). W— множество букв русского алфавита:

W= {А;Б;В;Г;Д;Е;Ж;З;И;Й;К;Л;М;Н;О;П;Р;С;Т;У;Ф;Х;Ц;Ч;Ш;Щ; Ь;Ы;Ъ;Э;Ю;Я }

Для обозначения элементов множества используют малые буквы латинского алфавита.

Например: 1). f = 6 – элемент множества цифр.

2). а = Р -- – элемент множества букв русского алфавита.

Принадлежность предмета данному множеству обозначается Є , а непринадлежность – символом Є .

Например:1). f = 6 ; 6 є А, где А— множество цифр.

2). S є W, где W— множество букв русского алфавита.

Множество может быть: 1). Конечное : Например: А— множество цифр.

2). Бесконечное: Например: N – множество натуральных чисел.

3). Пустое: ø-- множество, в котором нет ни одного элемента.

Если множество В состоит из некоторых элементов множества А (и только из них), то множество В называется ПОДМНОЖЕСТВОМ множества А.

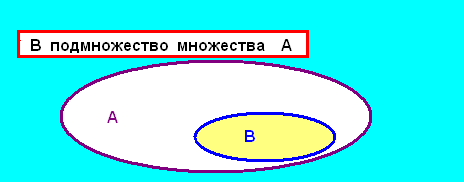
Например:1). В= {5;9;0 }, А= { 0;1;2;3;4;5;6;7;8;9 }, то В А (читается В содержится в А).

2). С= { Л;Е;Т;О },

W= {А;Б;В;Г;Д;Е;Ж;З;И;Й;К;Л;М;Н;О;П;Р;С;Т;У;Ф;Х;Ц;Ч;Ш;Щ; Ь;Ы;Ъ;Э;Ю;Я },

то С W (С содержится в W).

Способы задания множеств: 1) перечислением его элементов;

2) описанием характеристического свойства его элементов.

Например: 1). К= {х : -5 ≤ х ≤ 6 }.

2). Т= {х : 0 ≤ х ≤ 9, х є N }.

Множества называются РАВНЫМИ, если они состоят из одних и тех же элементов.

Например: 1). Множество корней уравнения х²=49; L= {-7;7 },

Множество корней уравнения | х |=7; M= {-7;7 }, = L=М.

-- Решение задач:

1.Задайте перечислением элементов множества:

а) А—множество гласных букв русского алфавита.

б) В—множество корней уравнения х³-4х²=0.

в) С—множество простых четных чисел.

г) D— множество времен года.

2. Запишите несколько элементов каждого множества:

а) А={ х : х=2m+1}.

б) В= {х : х=2 m }.

в) С= {х : 0 ≤ х ≤ 1 }

3. Перечислить элементы следующих множеств:

а) А= {х : хє ученикам вашего класса, которые сейчас отсутствуют }.

б) В= { х : (х-2)(х+3)=0 }.

в) С= { х : х²-8х+15=0 }.

4. Какие из следующих множеств являются пустыми:

а) множество решений уравнений х²-4=0.

б) множество решений уравнений х=х+2.

в) множество решений уравнений х+1 = х+1.

г) множество кругов, у которых диаметр меньше радиуса.

5. Даны множества:

а) множество А всех трапеций.

б) множество В всех прямоугольников.

в) множество С всех четырехугольников.

г) множество D всех квадратов.

д) множество H всех параллелограммов.

е ) множество F всех многоугольников.

Запишите с помощью знака эти множества в таком порядке, чтобы каждое последующее множество являлось подмножеством предыдущего.

Восприятие нового материала:

ОПЕРАЦИИ НАД МНОЖЕСТВАМИ

ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ А и В – это множество С, состоящее из всех тех и только тех элементов, которые принадлежат каждому из данных множеств А и В. Обозначают: С=А∩В.

Например: L= { 5;7;9;3;1}, W= { 1;0;8;2;4;5;6 } = L ∩ W= { 1;5 }=К.

Схематически можно изобразить c помощью кругов Эйлера:

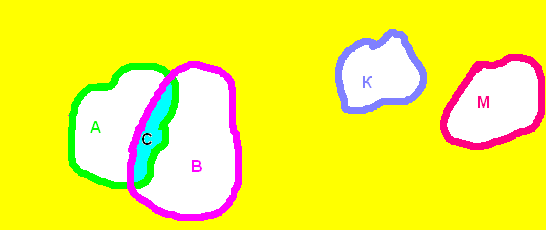
С= А ∩ В К ∩ М = ø

Решение задач:

1. Дано: А= {а;с;к;1;3 }, В= {с;е;6;3 }, С= {с;1;6 }.Найти: а)А∩В; б)А∩С; в) В∩С; г) А∩В∩С.

2. Дано: А={ х : х²-5х+6=0}, В={ х : х²-3х+2=0}. Найти А∩В.

Восприятие нового материала:

ОБЪЕДИНЕНИЕ МНОЖЕСТВ А и В – это множество С, состоящее из всех элементов множеств Аи В и только из них. Обозначают: С=А U B.Если множества имеют одинаковые элементы, то каждый из этих элементов берется один раз.

Например: L= { 5;7;9;3;1}, W= { 1;0;8;2;4;5;6 } = L U W= { 0;1;2;3;4;5;6;7;8;9 }.

Схематически можно изобразить c помощью кругов Эйлера:

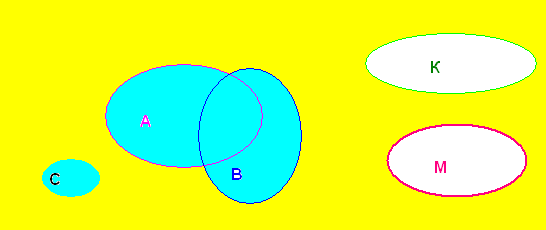
С=А U B К U M = ø

Решение задач:

1.Дано: А={1;3;5;7}, В={1;5;7;9}, С={2;4}. Найти: а) А U В; б) А U С; в) В U С; г) А U В U С.

2.Дано: А= { х : х²-5х+6=0 }, В= {х : х²-3х+2 }. Найти: А U В.

Восприятие нового материала:

РАЗНОСТЬ МНОЖЕСТВ А и В – это множество, состоящее из всех элементов множества А, не принадлежащих множеству В. Обозначают: С = А\ В.

Схематически можно изобразить c помощью кругов Эйлера:

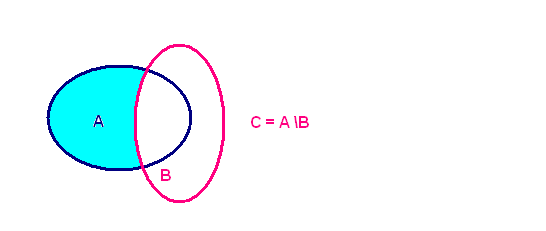
Решение задач:

1. Дано: M = { a;b;c;d } , N = { b;d } .Найти: а) M \ N; б) N \ M; в) (M \ N) U (N \ M).

Разность множеств К = {1;2;3;7;8;9;) } и М = {2;0;8 }.

Подведение итогов урока:

? приведите примеры множеств.

Какие бывают множества по количеству элементов?

Как обозначаются множества?

Как обозначается принадлежность или непринадлежность элемента данному

множеству?

Какими способами задаются множества (привести примеры) ?

Какие множества называются равными (привести примеры) ?

Какое множество называется подмножеством данного множества ( привести примеры и

записать их символически) ?

Что называется пересечением двух множеств ( привести примеры и записать

символически ) ?

Что называется объединением двух множеств ( привести примеры и записать

символически ) ?

Что называется разностью двух множеств ( привести примеры и записать

символически ) ?

Д/З

№1.

1)Записать множество чисел кратных 7, не превосходящих 60. {7;14;21;28;35;42;49;56}

Отв: { 7;14;21;28;35;42;49;56 }

2) Найти множество корней уравнения: х²-3х-10=0;

D=9-4∙1∙(-10)=7²; х =(3+7):2=5; х = (3-7):2= --2 ; Отв: { -2; 5 }

№2.

Выписать все подмножества множества М = { 5;12; 6}.

Отв: ø , {5}, {12}, {6}, {5;12}, {5;6}, {12;6}, {5;12;6}.

№3.

Найдите объединение и пересечение множеств корней уравнений: х²-3х+2=0; х²-1=0;

А = {1;2} В = { -1;1} Отв: А Ụ В = {-1;1;2}, А ∩ В = { 1 }.

№4.

Найдите А \ В и В \ А.

А ={a;b;c;d}, B = { b;d;p;q;r }. Отв: А \ В = {а;с} , В \ А = { p;q;r }.

5