Тема: «Логарифмы и их свойства. Логарифмическая функция. Решение логарифмических уравнений и неравенств»
Цели занятия:
Образовательная: рассмотреть понятие логарифма числа и свойства логарифмов; дать понятие десятичного и натурального логарифма; овладеть знаниями и умениями использовать основное логарифмическое тождество, формулы перехода от одного основания к другому в процессе решения упражнений.
Развивающая: развивать мышление учащихся при выполнении упражнений; продолжить формировать умение правильно воспринимать и активно запоминать новую информацию; научить учащихся определять логарифм числа и его свойства; вычислять значения несложных логарифмических выражений.
Воспитательная: побудить интерес к изучению предмета.
Краткое содержание лекции
Логарифмы и их свойства.
Логарифмическая функция.
Решение логарифмических уравнений и неравенств.
Ход занятия
Организация занятия _______________________________5 мин
Изложение плана и методики проведения занятия _____5мин
Лекционная часть _________________________________75мин
Подведение итога занятия __________________________5мин
Рассмотрим уравнение ax = b, при a 0 и a не равном единице. Это уравнение не имеет решений при b меньшем либо равным нулю. И имеет единственное решение при b 0. Данное решение называют логарифмом b по основанию a b и обозначают следующим образом: loga(b)
Логарифмом числа b по основанию f называется показатель степени, в которую необходимо возвести число а, чтобы получилось число b.
a(loga(b)) = b.
Данная формула называется основным логарифмическим тождеством. Она верна для любого положительного не равного единице a, и любого положительного b.
Примеры логарифмов
Рассмотрим несколько примеров:
1. Найти значение log2(32). 32 можно представить как 25. То есть для того, чтобы нам получить число 32, необходимо двойку возвести в пятую степень. Следовательно, log2(32) = 5.
2. Найти логарифм числа 1/9 по основанию √3. Так как (√3)4 = 1/9, получаем, что log√3(1/9) = -4.
3. Найти х такое, что будет верно неравенство: log8(x) = 1/3. Применим основное логарифмическое тождество:
x = 8(log8(x)) = 8(1/8) = 2.
Свойства логарифмов
У логарифмов есть несколько свойств, которые прямо следуют из свойств показательной функции. Основные свойства логарифмов:
1. loga(1) = 0;
2. loga(a) = 1;
3. loga(x*y) = loga(x) + loga(x) - логарифм произведения равен сумме логарифмов;
4. logx(x/y) = loga(x) - loga(y) - логарифм частного равен разности логарифмов;
5. loga(xp) = p* loga(x) - логарифм степени будет равен произведению показателя степени на логарифм основания этой степени.
Приведенные выше свойства будут справедливы для любого положительного числа а, не равного единице, любых положительны x и y, и любого действительного p.
Для логарифмов существует формула перехода к новому основанию:
loga(x) = (logb(x))/(logb(a)).
Данная формула будет иметь смысл лишь в том случае, когда обе её части будут иметь смысл. То есть должны выполняться следующие условия:
x 0, a 0,b 0, a не равно единице, b не равно единице.
Логарифмы основанием которых является число 10, называются десятичными логарифмами. Логарифмы, основанием которых является число e, называются натуральными логарифмами.
Функцию вида y = loga(x), где a любое положительное число не равное единице, называют логарифмической функцией с основанием а. Здесь и далее для обозначения логарифма мы будем использовать следующую нотацию: loga(b) - данная запись будет обозначать логарифм b по основанию а.
Основные свойства логарифмической функции:
1. Областью определения логарифмической функции будет являться все множество положительных вещественных чисел. Для краткости его еще обозначают R+. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию а.
2. Областью значения логарифмической функции будет являться все множество вещественных чисел.
3. Если основание логарифмической функции a1, то на всей области определения функции возрастает. Если для основания логарифмической функции выполняется следующее неравенство 0
4. График логарифмической функции всегда проходит через точку (1;0).
5. Возрастающая логарифмическая функция, будет положительной при x1, и отрицательной при 0
6. Убывающая логарифмическая функция, будет отрицательной при х1, и положительной при 0
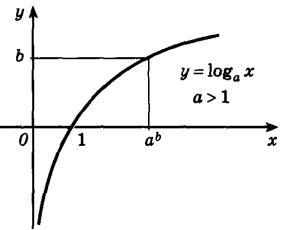
На следующем рисунке представлен график убывающей логарифмической функции - (0
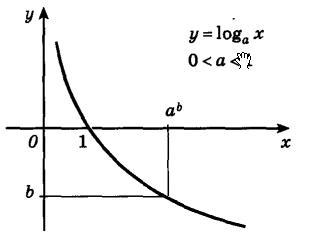
7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид.
8. Функция не имеет точек максимума и минимума.
Если построить в одной оси координат показательную и логарифмическую функции с одинаковыми основаниями, то графики этих функций будут симметричны относительно прямой y = x. Данное утверждение показано на следующем рисунке.
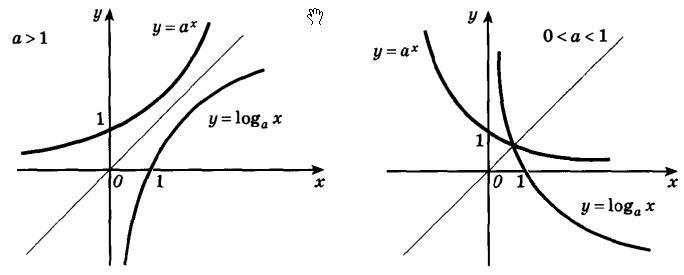
Рассмотрим пример: найти область определения логарифмической функции f(x) = log8(4 - 5*x).
Исходя из свойств логарифмической функции, областью определения является все множество положительных вещественных чисел R+. Тогда заданная функция будет определена для таких х, при которых 4 - 5*x0. Решаем это неравенство и получаем x
Таким образом, получается, что областью определения функции f(x) = log8(4 - 5*x) будет являться промежуток (-∞;0.8)
Логарифмическое уравнение — уравнение, в котором неизвестные переменные находятся внутри логарифмов.
Простейшим логарифмическим уравнением является уравнение вида loga x = b.
Основные методы решения логарифмических уравнений:
1 метод. Использование определения логарифма:
2 метод. Использование свойств логарифма:
logacb=1clogab
c⋅logab=logabc
logab+logac=loga(bc)
logab−logac=loga(bc)
loganb=1n⋅logab
loganbm=mn⋅logab
loga1=0, a0,a≠1
logaa=1 (a0,a≠1)
3 метод. Введение новой переменной (замена):
4 метод. Переход к новому основанию:
5 метод. Логарифмирование:
Что такое логарифмические неравенства?
Определение: Простейшим логарифмическим неравенством является соотношение вида:
loga f(x) logag(x),
где f(x) и g(x) – некоторое выражение, зависящее от x (например, f(x)=1+2x+x2, g(x)=3x−1).
Решение логарифмических неравенств
Теперь запишем правило:
| loga f(x) loga g(x) = f(x)g(x) при a1 logaf(x) loga g(x) = f(x)g(x) при 0a |
Если сказать все простыми словами, то: если основание логарифма в неравенстве больше единицы, то знак неравенства сохраняется и для f(x) иg(x), если же основание логарифма больше нуля и меньше единицы, то знак между f(x) и g(x) заменяется на противоположный.


 Получите свидетельство
Получите свидетельство Вход
Вход















 Разработка урока по математике «Логарифмы и их свойства. Логарифмическая функция. Решение логарифмических уравнений и неравенств» (52.16 КB)
Разработка урока по математике «Логарифмы и их свойства. Логарифмическая функция. Решение логарифмических уравнений и неравенств» (52.16 КB)
 0
0 1321
1321 117
117 Нравится
0
Нравится
0


