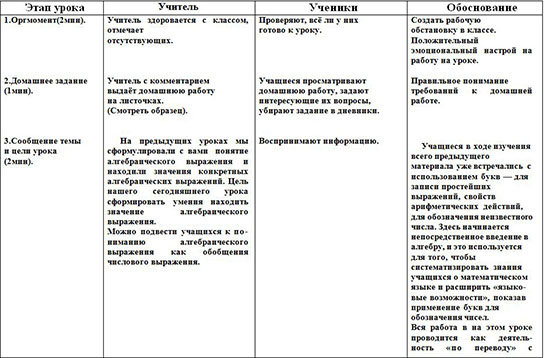
| 1.Оргмомент(2мин).
2.Домашнее задание (1мин).
3.Сообщение темы и цели урока (2мин).
4.Разминка(5мин). Игровой момент: «Математический пинг-понг»
5.Закрепление полученных навыков(5мин).
6.Работа с таблицей (3 мин). Творческое задание.
7.Закрепление полученных навыков с помощью задачи исследовательского содержания(4мин). «Нестандартная задача»
9.Физкультминутка (1мин).
10. Работа с таблицей на нахождение значений алгебраических выражений(10мин).
11. Самостоятельная работа по учебнику
12.Подведение итогов(3мин).
ЭСКИЗ ПЛАКАТА | Учитель здоровается с классом, отмечает отсутствующих.
Учитель с комментарием выдаёт домашнюю работу на листочках. (Смотреть образец).
На предыдущих уроках мы сформулировали с вами понятие алгебраического выражения и находили значения конкретных алгебраических выражений. Цель нашего сегодняшнего урока сформировать умения находить значение алгебраического выражения. Можно подвести учащихся к пониманию алгебраического выражения как обобщения числового выражения.
На доске записано выражение: -18а. Учитель задает кратко вопросы: 1) Коэффициент? 2) Разбейте на два равных слагаемых. 3) Разбейте на два неравных слагаемых. 4) Разбейте на три равных слагаемых. 5) Разбейте на три неравных слагаемых. 6)Разбейте на два множителя. 7) Разбейте натри множителя. 8) Найдите значение выражения — 18а, если: а=1, 0, -2 Математический диктант утроенное произведение чисел а и b частное от деления чисел m и n разность числа b и половины числа с Необходимо обратить внимание учащихся на возможность разных записей: ½с, с:2, с/2, 0,5с
Каждое из выражений — 4а; —За; — 2а; — а; 0; а; 2а; За; 4а запишите в клетки квадрата так, чтобы после приведения подобных членов по любой горизонтали, вертикали и диагонали получился нуль.
Однажды Витя Верхоглядкин получил на дом такое задание: «Найдите значение выражения 3(2х —8) —4(1,5х —8,5) при х=1; —3; 5». Витя принялся за работу. Он подставил в данное выражение вместо буквы х число 1, выполнил действия, получил 10. Подставил число —3, получил 10. Подставил 5, и у него опять получилось 10. «Какое странное выражение,— подумал Витя,— всегда получается 10. Но я найду такое число, чтобы значение этого выражения оказалось равным другому числу». И он стал вместо х подставлять разные числа. Но, к его удивлению, в ответе всегда получалось 10. Он просидел весь вечер, но так и не добился своего. Как вы думаете, ребята, почему?
С целью функциональной пропедевтики (для подготовки формирования представлений о функции как зависимой переменной, о значениях аргумента и функции) можно предложить учащимся заполнить таблицу значений алгебраических выражений, содержащих в своей записи только букву х, при различных значениях х.
№12 (1,3) [ №12 (2,3) ] №15(1) [ №15(2)] Первое задание на нахождение значения выражения, а второе – на его запись по словесной формулировке.
Всё ли понято в теме? На чём ещё нужно остановиться? | Проверяют, всё ли у них готово к уроку.
Учащиеся просматривают домашнюю работу, задают интересующие их вопросы, убирают задание в дневники.
Воспринимают информацию.
Ученики должны отвечать быстро, практически не задумываясь:
—18. — 9а + ( — 9а).
— 10а + ( — 8а).
— 6а + ( - 6a)+ (- 6a).
- a + ( -3а)+ 22a
— 6 ∙Зa. — 2∙3∙За.
-18, 0, 36. ЗаЬ т:п b-½c На дополнительных досках работают два ученика. После выполнения работы Ученики комментируют полученные ответы. Остальные решают в тетрадях, потом сверяют свои решения с решениями на доске. Обнаруженные ошибки исправляются.
Заполняют таблицу:
| а
|
2a |
-3a | |
-4a | 0
| 4а
| |
3a |
-2a |
-a
|
После некоторых размышлений ребята, скорее всего, должны предложить упростить выражение. Если этого не произошло, сделать правильные выводы им должен помочь учитель. Упростив выражение выясняется, что в нём получается 10 и оно не зависит от букв.
Выполняют.
Дети работают в парах. Самые быстро справившиеся выходят к доске заполнять заранее заготовленный плакат с таблицей. Далее идет взаимопроверка, исправление ошибок, если таковые имеются.
Решают и сдают на проверку учителю. -1; -0,47; -35; -0,975; 0,66(а+4,02) 0; -12,1; -35; -0,975; 0,33(х/0,27)
Дети дают ответы. | Создать рабочую обстановку в классе. Положительный эмоциональный настрой на работу на уроке.
Правильное понимание требований к домашней работе.
Учащиеся в ходе изучения всего предыдущего материала уже встречались с использованием букв — для записи простейших выражений, свойств арифметических действий, для обозначения неизвестного числа. Здесь начинается непосредственное введение в алгебру, и это используется для того, чтобы систематизировать знания учащихся о математическом языке и расширить «языковые возможности», показав применение букв для обозначения чисел. Вся работа в на этом уроке проводится как деятельность «по переводу» с обычного русского языка на математический и обратно. Активизация познавательного интереса учащихся.
Такой игровой момент значительно способствует умению подвижно мыслить, развивает реакцию, позволяет задать темп уроку.
Задание предполагающие творческо-преобразующую деятельность детей. Актуализация имеющихся знаний учащихся. Повышение заинтересованности в знаниях. Работает долговременная память.
Оперативный контроль за решением. Оценивание.
Развитие качеств мышления: самостоятельности, активности, убедительности. Повторение свойств арифметических действий
Задача развивающего характера. Задана нестандартно. Развивает логику, аналитическое мышление. Перенос знаний в нестандартную ситуацию. Развитие творческих способностей.
Профилактика утомления
Отработка решения с помощью наглядного материала. Работает долговременная память.
Контроль за уровнем усвоения материала. Развитие умения выслушивать ответы товарищей. Осуществление оперативного контроля. Воспитание самоконтроля Воспитание доброжелательности, уважения друг к другу.
Осуществление индивидуального контроля.
Рефлексия. Нужна для дальнейшего планирования материала. |
Получите свидетельство
Вход
Разработка урока по математике "Алгебраические выражения" (0.12 MB)
0
1100
53
Нравится
0
