Разработка методических рекомендаций обучению учащихся решению задач по математике «Применение производной к исследованию функций»

Введение.

Сегодня мы сталкиваемся с парадоксальной ситуацией: школа бурно развивается, меняется, а педагогические технологии, программы отстают от этого процесса. Недостаточно реализуется потенциал социальной педагогики в процессах развития школьников, как граждан, имеющих определенные жизненные ориентации.

Актуальность темы обусловлена рядом противоречий между современной системой обучения школьников и требованиями ФГОС ООО второго поколения.

Во-первых, анализ деятельности общеобразовательных школ, потребности рынка труда и научные источники показывают на необходимость изменения подхода к результатам обучения, рассматривая их как достижение школьниками личностных результатов, включающих «готовность и способность обучающихся к саморазвитию и личностному самоопределению, сформированность их мотивации к обучению и целенаправленной познавательной деятельности, системы значимых социальных и межличностных отношений, ценностно-смысловых установок, отражающих личностные и гражданские позиции в деятельности, социальные компетенции, правосознание, способность ставить цели и строить жизненные планы, способность к осознанию российской идентичности в поликультурном социуме».

Во-вторых, анализ работы методических служб общеобразовательных школ показывает, что при существующем требовании общества к образованию и воспитанию  молодёжи, отмечается несовершенство программ, недостаток методических материалов по организации обучения математике с целью достижения предметных и метапредметных результатов, предусмотренных ФГОС.

В-третьих, в настоящее время все ярче проявляется социальное расслоение общества, поэтому дети в семье имеют различную степень взаимопонимания, заинтересованности их будущим, а значит и создания предпосылок для жизненного самоопределения. Педагог же в своей работе, как правило, ориентируется только на личность с высоким уровнем мотивации или социальной активности.

Также на сегодняшний день и ряд других неразрешенных противоречий, касающихся общепедагогических задач:

- достаточно проработаны теоретические вопросы по внедрению ФГОС ООО, но отсутствует механизм его практического внедрения в общеобразовательный процесс; творческий потенциал большинства талантливых педагогов остается нереализованным;

- увеличивается объем информации, отмечается тенденция ориентации педагогов на формирование творческой личности обучающегося, однако используется традиционный набор педагогических технологий.

От того, насколько эффективно будут разрешены эти противоречия,  будет зависеть результат внедрения ФГОС, а в итоге качество российского образования.

Таким образом, востребованность социальной практикой и недостаточный уровень разработанности методик реализации ФГОС ООО и их преемственности в старшей школе, технологий ведения такой работы с учащимися средней школы обусловили выбор темы, предопределили объект, предмет, цель и задачи исследования.

Объект исследования: процесс обучения учащихся 10-х классов курсу алгебры и начал анализа общеобразовательной школы.

Предмет исследования: процесс обучения теме «Применение производной к исследованию функций» с учётом преемственности требований ФГОС ООО.

Цель работы:

разработать рекомендации для обучения учащихся теме «Применение производной к исследованию функций», реализующие преемственность требований ФГОС ООО.

Задачи работы:

1. анализ педагогической, учебно-методической и математической литературы по теме «Применение производной к исследованию функций»

2. анализ ФГОС учебников и школьных программ.

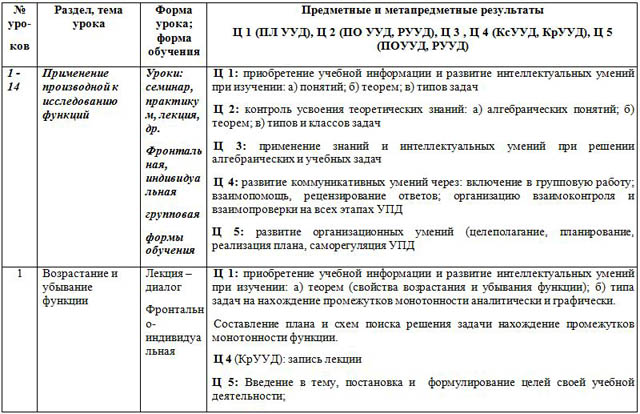
3. разработка методических рекомендаций обучению теме «Применение производной к исследованию функций».

4. составление набора задач.

Решение поставленных задач потребовало использования следующих методов исследования: анализ психолого-педагогической, математической и методической литературы по проблеме исследования, учебников и учебных пособий по алгебре и началам анализа.

Глава 1. Теоретические основы обучения теме «Применение производной к исследованию функций»

§ 1. Требования к содержанию рабочих программ в применении к школьному курсу математики в соответствии с Концепцией духовно-нравственного развития и воспитания личности гражданина России.

Необходимость написания данной Концепции определена тем, что «в российском обществе стал ощущаться недостаток сознательно принимаемых большинством граждан принципов и правил жизни, согласия в вопросах корректного и конструктивного социального поведения, а также отсутствие созидательных ориентиров смысла жизни».

Воспитание человека, формирование свойств духовно развитой личности, любви к своей стране, потребности творить и совершенствоваться есть важнейшее условие успешного развития России.

Концепция формулирует социальный заказ современной общеобразовательной школе как определенную систему общих педагогических требований, соответствие которым обеспечит эффективное участие образования в решении важнейших общенациональных задач.

Выполнению данного социального заказа должны служить рабочие программы математических курсов, в том числе элективных, цель которых - ориентация на индивидуализацию обучения и социализацию учащихся, на подготовку к осознанному и ответственному выбору сферы будущей профессиональной деятельности. Среди требований к содержанию программ выделим соответственно:

- наличие социальной и личностной значимости, актуальности как с точки зрения подготовки квалифицированных кадров, так и для личностного развития учащихся;

- помощь в социализации и адаптации учащихся, предоставление возможности для выбора индивидуальной образовательной траектории, осознанного профессионального самоопределения;

- поддержка изучения базовых и профильных общеобразовательных предметов, а также обеспечение условий для внутрипрофильной специализации обучения;

- значительный развивающий потенциал.

Для реализации целей математических курсов ведущее место в обучении следует отвести методам поискового и исследовательского характера, стимулирующим познавательную активность учащихся. Значительной должна быть доля самостоятельной работы с различными источниками учебной информации.

Успешность реализации Концепции духовно-нравственного развития и воспитания будет обеспечиваться приоритетом методик преподавания математических, в том числе элективных,  курсов: междисциплинарной интеграции, обучения через опыт и сотрудничество, интерактивности (работа в малых группах, имитационное моделирование, метод проектов), личностно - деятельностного подхода в обучении.

Программы математических курсов должны:

1) обеспечивать достижение планируемых результатов освоения основной образовательной программы;

2) ориентировать образовательный процесс на духовно-нравственное развитие и воспитание обучающихся;

3) обеспечивать комплексный подход к оценке, позволяющий вести оценку предметных, метапредметных и личностных результатов;

4) обеспечивать оценку динамики индивидуальных достижений обучающихся;

5) предусматривать использование разнообразных методов и форм, взаимно дополняющих друг друга (стандартизированные письменные и устные работы, проекты, практические работы, творческие работы, самоанализ и самооценка, наблюдения).

Весь материал - в документе.