Математическая речь развивается на протяжении всего периода обучения в школе, но особое внимание ей уделяется в начальной школе, так как именно в начальной школе дети впервые сталкиваются с математическими понятиями и выражениями, знакомятся с основными математическими правилами, так же закладывается фундамент по формированию математической культуры речи. Оптимальное применение математических терминов способствует глубокому пониманию учебного процесса и стимулирует быстрое совершенствование мыслительных способностей, а также поддерживает логическое умозаключение и развивает восприятие пространства. Одной из конечных целей математики в начальной школе является формирования математической грамотности, с помощью общения на математическом языке. Умение распознавать проблемы учеником решается с помощью формулирования их на математическом языке. Так как математика является точной наукой, в этой связи детей следует приучать к избеганию слов, не несущих смысловой нагрузки. Правильное методическое применение математических терминов способствует осмысленному подходу к образовательному процессу и обеспечивает ускорение мышления обучающегося [36].
Начальный курс математики является курсом интегрированным: в нём объединён арифметический, геометрический и алгебраический материал.
Содержание обучения в 1 классе представлено в программе разделами: «Числа и величины», «Арифметические действия», «Текстовые задачи», «Пространственные отношения. Геометрические фигуры», «Математическая информация». Особенностью этой программы является фиксирование круга понятий и терминов, которыми должны овладеть младшие школьники на каждом этапе обучения [5].
В 1 классе на уроках математики в разделе «Числа и величины» предметами изучения являются следующие направления: числа от 1 до 9: различение, чтение, запись; единица счёта; десяток; счёт предметов, запись результата цифрами; число и цифра 0 при измерении, вычислении; числа в пределах 20: чтение, запись, сравнение; однозначные и двузначные числа; увеличение (уменьшение) числа на несколько единиц; длина и её измерение; единицы длины и установление соотношения между ними: сантиметр, дециметр; литр; килограмм [41].
На уроках математики в 1 классе могут быть использованы следующие задания:
Величина. Педагог раздает карточки с заданием (табл. 2.2.), на каждой карточке написаны задачи, но не указаны единицы измерения, задача обучающегося заключается в том, что ему нужно указать наименование единиц измерения для каждой задачи. В качестве проверки такого задания, следует спросить нескольких обучающихся, как они выполняли задание и что выбрали, это будет способствовать закреплению темы, запоминанию единиц измерения, так как они их не только проговорят вслух, но и напишут на карточке, а также расширению математического активного запаса слов.
Таблица 2.2
«Величины»
| Задачи |
| Катя начертила отрезок 4…, а Федя продолжил этот отрезок, начертив еще 2 … . Какой длины получился отрезок? |
| Ящик со свежими овощами весит 13…, а коробка с фруктами легче на 4 … . Сколько весит коробка с фруктами? |
| Мама купила 7 … ленты, 4 … ленты она израсходовала на банты для дочери. Сколько … ленты осталось у мамы? |
| Масса тыквы 8 …, а масса кабачка 1… . Насколько тыква тяжелее кабачка? |
| В одной ведре помещается 5 … воды, а в другом 3… . Сколько … воды получится, если оба ведра будут полные? |
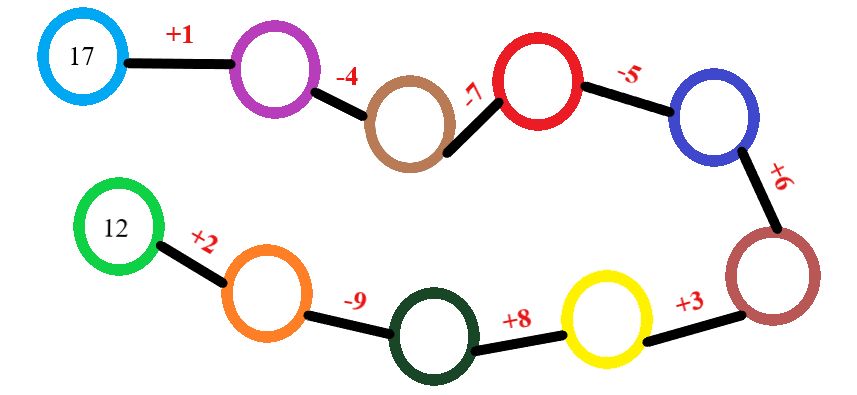
Математическая змейка. На доске нарисованы шарики, расположенные в виде змейки. В первом шарике написано какое-то число, шариков может быть любое количество, между собой шарики соединены, над каждым соединением написан математический знак и число. В этой игре участники формируют цепочку, во время которой каждый ребенок по очереди выбирает математическое задание и вычисляет его решение. Результат каждого вычисления фиксируется в специальном шарике, и процесс продолжается, пока не исчерпаются все доступные шарики. Пример математической змейки представлен на рисунке 2.1.
| | |
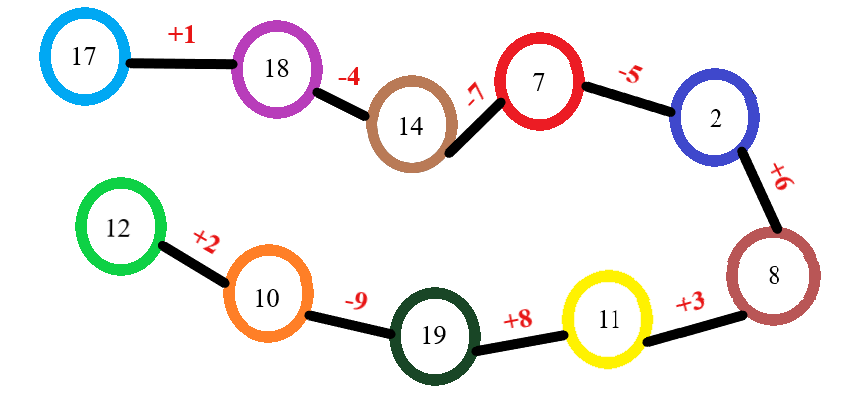
Рис. 2.1. Задание и ответы к упражнению «Математическая змейка»
В качестве усложнения задания можно вместо ответов в шариках записать знак и число, а дети должны на слух воспринимать и запоминать ответы предыдущих детей.
Математический шарфик. Задание направлено на базовое логическое действие: установление связи и зависимости между числами. На математическом шарфе числа записаны по определенному правилу, учащимся нужно определить и озвучить правило, а также записать пропущенные числа. Пример математического шарфика представлен на рисунке 2.2.

Рис. 2.2. Упражнение «Математический шарфик»
Математические ребусы. Задание заключается в следующем, обучающимся раздаются ребусы им нужно не только сосчитать и записать ответ, но и объяснить алгоритм выполнения ребуса. Пример ребуса представлен на рисунке 2.3.
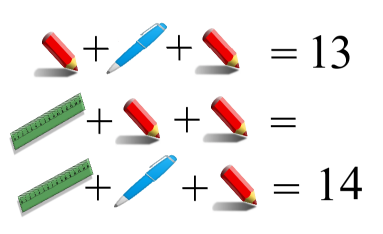
Рис. 2.3. Математический ребус
Сравнение величин. Обучающимся раздается карточка с заданием, на которой начерчены отрезки, которые представлены на рисунке 2.4. Учитель предлагает с помощью линейки измерить предоставленные им отрезки и ответить на следующие задания, например:
Найдите самый короткий отрезок.
Чему равен отрезок СН или AC?
Найдите самый длинный отрезок.
Чему равен отрезок DE?
Найдите средний отрезок?
Чему равен отрезок KM?
Какими отрезками являются отрезки СН и AC?
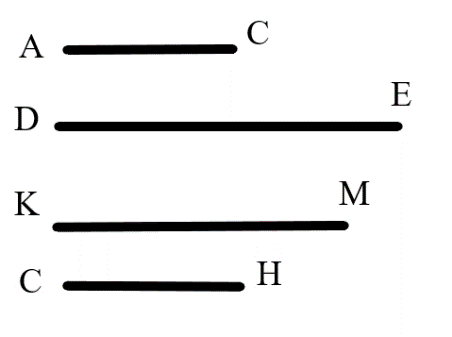
Рис. 2.4. Упражнение на сравнение величин

 Получите свидетельство
Получите свидетельство Вход
Вход












 Разработка комплекта заданий по математике для 1 класса (125.31 KB)
Разработка комплекта заданий по математике для 1 класса (125.31 KB)
 0
0 300
300 1
1 Нравится
0
Нравится
0


