Разбор варианта ЕГЭ по математике

Презентация будет незаменима на уроках математике в старшей школе при подготовке к ЕГЭ. Так же будет полезна при последних консультациях перед экзаменом.

В презентации каждое задание части В имеет формулировку, чертеж (при необходимости) и решение. 

Особенностью данной учебной презентации является наличие подробного и понятного решения каждой задачи части В.

Строительный подрядчик планирует купить 5 тонн облицовочного кирпича у одного из трех поставщиков. Вес одного кирпича 5 кг. Цены и условия доставки приведены в таблице. Во сколько рублей обойдется наиболее дешевый вариант покупки?

Решение.
Необходимо купить 5000 : 5 = 1000 кирпичей. 

Рассмотрим все варианты. 

При покупке у поставщика A стоимость заказа складывается из стоимости кирпича 17  1000 = 17 000 руб. и стоимости доставки. Всего 17 000 + 7000 = 24 000 руб. 

При покупке у поставщика Б стоимость заказа складывается из стоимости кирпича 18  1000 = 18 000 руб. и стоимости доставки и равна 18 000 + 6000 = 24 000 руб. 

При покупке у поставщика В стоимость заказа складывается из стоимости кирпича 19  1000 = 19 000 руб. и стоимости доставки и равна 19 000 + 5000 = 24 000 руб. 

Во всех трех вариантах стоимость равна 24 000 руб. 

Ответ: 24 000.

РЕШЕНИЕ ВАРИАНТА ЕГЭ ПО МАТЕМАТИКЕ

Кравченко Н.А.

Учитель математики

ГБОУ СОШ №891,

г. Москва

В1

Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей? 

Решение. С учетом наценки учебник будет стоить 170 + 0,2 * 170 = 204 рубля. Разделим 7000 на 204: 

Значит, можно будет купить 34 учебника.  Ответ: 34.

В2

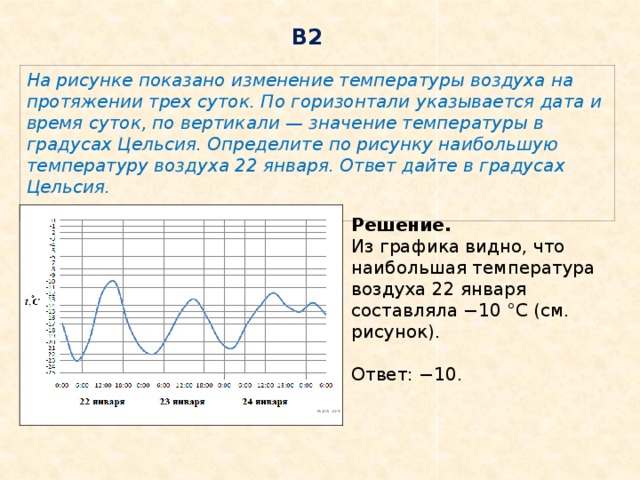
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 22 января. Ответ дайте в градусах Цельсия.

Решение. Из графика видно, что наибольшая температура воздуха 22 января составляла −10 °C (см. рисунок).

  Ответ: −10.

В3

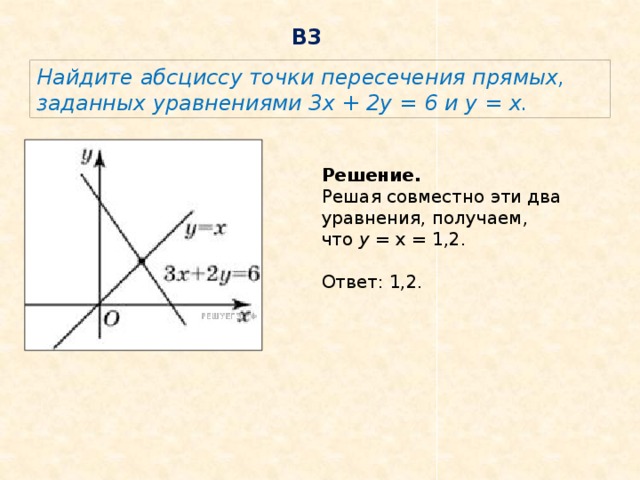
Найдите абсциссу точки пересечения прямых, заданных уравнениями 3x + 2y = 6 и y = x.

Решение. Решая совместно эти два уравнения, получаем, что  у  = x = 1,2. 

Ответ: 1,2.

В4

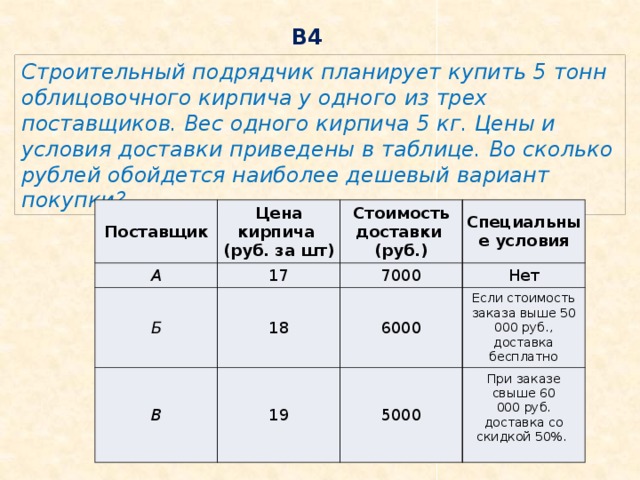
Строительный подрядчик планирует купить 5 тонн облицовочного кирпича у одного из трех поставщиков. Вес одного кирпича 5 кг. Цены и условия доставки приведены в таблице. Во сколько рублей обойдется наиболее дешевый вариант покупки?

Поставщик

Цена кирпича  (руб. за шт)

А

17

Б

Стоимость доставки  (руб.)

7000

Специальные условия

18

В

19

Нет

6000

Если стоимость заказа выше 50 000 руб., доставка бесплатно

5000

При заказе свыше 60 000 руб. доставка со скидкой 50%. 

Решение. Необходимо купить 5000 : 5 = 1000 кирпичей.  Рассмотрим все варианты.  При покупке у поставщика  A  стоимость заказа складывается из стоимости кирпича 17  1000 = 17 000 руб. и стоимости доставки. Всего 17 000 + 7000 = 24 000 руб.  При покупке у поставщика  Б  стоимость заказа складывается из стоимости кирпича 18  1000 = 18 000 руб. и стоимости доставки и равна 18 000 + 6000 = 24 000 руб.  При покупке у поставщика  В  стоимость заказа складывается из стоимости кирпича 19  1000 = 19 000 руб. и стоимости доставки и равна 19 000 + 5000 = 24 000 руб.  Во всех трех вариантах стоимость равна 24 000 руб. 

Ответ: 24 000.

В5

Найдите корень уравнения .

Решение. Перейдем к одному основанию степени:

Ответ: 12,5.

В6

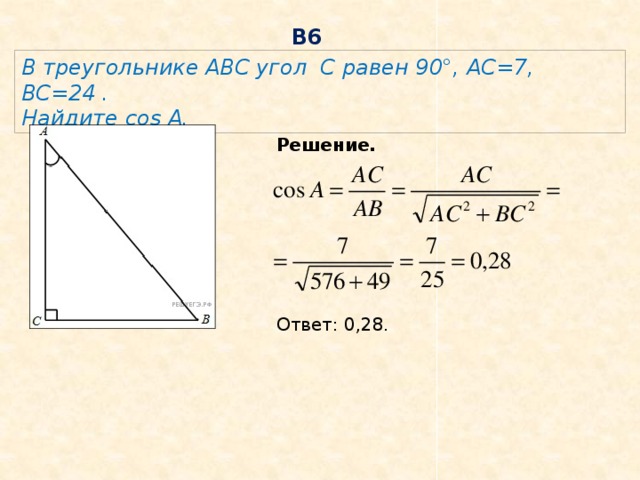
В треугольнике АВС угол  С равен 90°, АС=7, ВС=24 .

Найдите cos A.

Решение.

Ответ: 0,28.

В7

Вычислите значение выражения: .

Решение. Выполним преобразования:

Ответ: 3.

В8

На рисунке изображен график производной функции  , определенной на интервале (-8;3) . В какой точке отрезка

  [-3;2] функция   принимает наибольшее значение? 

Решение. На заданном отрезке производная функции отрицательна, поэтому функция на этом отрезке убывает. Поэтому наибольшее значение функции достигается на левой границе отрезка, т. е. в точке −3. 

Ответ: −3.

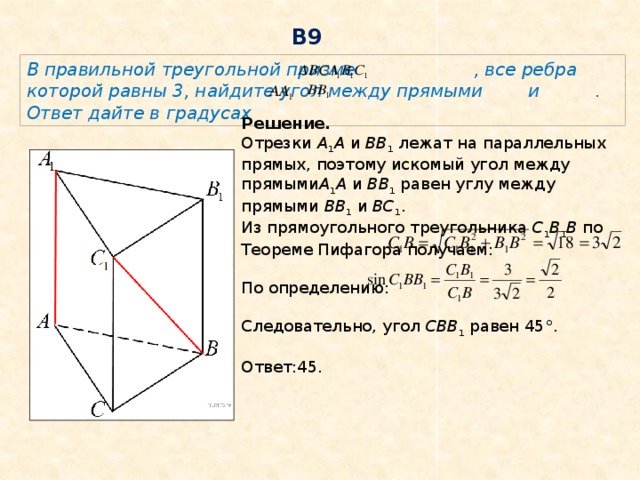
В9

В правильной треугольной призме   , все ребра которой равны 3, найдите угол между прямыми   и . Ответ дайте в градусах

Решение.

Отрезки  A 1 A  и  BB 1  лежат на параллельных прямых, поэтому искомый угол между прямыми A 1 A  и  BB 1  равен углу между прямыми  BB 1  и  BC 1 .  Из прямоугольного треугольника  C 1 B 1 B  по Теореме Пифагора получаем:

По определению:

Следовательно, угол  CBB 1  равен 45°.  

Ответ:45.

В10

В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.

Решение. Всего в соревнованиях принимает участие 4 + 7 + 9 + 5 = 25 спортсменов. Значит, вероятность того, что спортсмен, который выступает последним, окажется из Швеции, равна 

Ответ: 0,36.

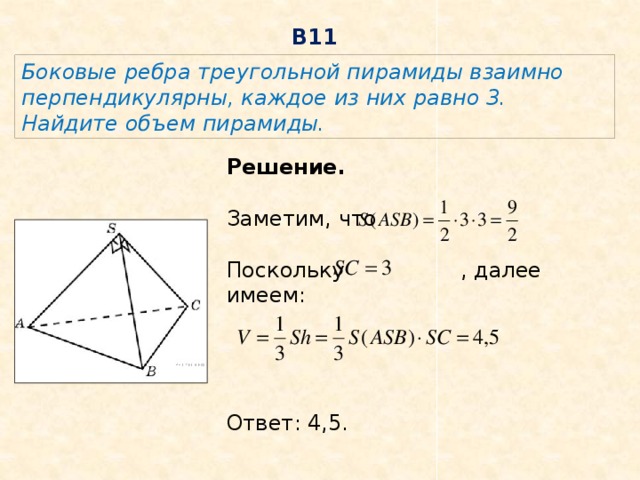
В11

Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

Решение.

Заметим, что 

Поскольку  , далее имеем:

Ответ: 4,5.

В12

Катер должен пересечь реку шириной L=100 м и со скоростью течения u=0,5 м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением  ,

где    – острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом  (в градусах) нужно плыть, чтобы время в пути было не больше 200 с?

Решение. Задача сводится к решению неравенства

   на интервале   при заданных значениях длины реки

L=100   м и скорости течения u=0,5   м/с:

Ответ: 45.

В13

Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам.

Решение. Пусть улитка проползла в первый день a1   метров, во второй – a2  , … , в последний –

   an метров. Тогда  a1+an=10  м, а за  n дней проползла    метров.

Поскольку всего она проползла 150 метров, имеем:  .

Таким образом, улитка потратила на весь путь 30 дней. 

Ответ: 30.

В14

Найдите точку минимума функции .

Решение. Квадратный трехчлен  с положительным старшим

коэффициентом достигает минимума в точке  , в нашем

случае — в точке 3. Поскольку функция   возрастающая, а заданная функция определена при найденном значении переменной, она достигает минимума в той же точке, в которой достигает минимума подкоренное выражение. 

Ответ: 3.

Материал взят с сайта www.reshuege.ru

Ссылка на использованный вариант: http://reshuege.ru/test?id=2433092&nt=True&pub=False