Решение типовых задач по информатике на тему “Исполнители”
Учитель математики и информатики Новиков А.В. (первая категория)
Тип 1

Решение:
Давайте сначала запишем наши команды в виде арифметических операций и операций сцепления:
1: +1
2: b* (* означает наше предыдущее число. Приписка слева, число b стоит перед числом, приписка справа, число b стоит после предыдущего числа).
Зададим начальное значение: по условию оно равно 2.
Построим таблицу. Первый столбик номер команды, второй столбик выражение, которое получилось при выполнении этой команды. Каждое новое выражение равно предыдущему выражению и выполнению команды. Количество строк равно шапке таблицы + начальное значение + количество узлов в числе (команд).
| Номер команды | Выражение |
| Начальное значение | 2 |
| 1 | 2+1=3 |
| 1 | 3+1=4 |
| 2 | b4 |
| 2 | bb4 |
| 1 | bb4+1 |
Последнее выражение bb4+1 приравняем к конечному числу.
bb4+1=775. Мы получили уравнение. Все, что с буквенной частью, оставим в левой части уравнения, в правую часть уравнения перенесем число. Правило переноса (переносим в противоположную часть уравнения, меняем знак). Получим:
bb4=775-1. bb4=774. Сверяем разряды узлов , где стоят b с разрядами узлов правой частью уравнения. Второй и первый разряд равен 7, следовательно b=7.
Задача решена.
Тип 2

Иногда бывают ситуации, когда напрямую высчитывать нецелесообразно. Получится громоздкое уравнение и сложно будет понять искомое число. Поэтому можно выполнить операции не с начала, а с конца. Но, имейте в виду, что если мы идем обратно, арифметические операции меняются. Если сложение, меняем на вычитание, и наоборот. Также работает и с умножением и делением.
Идем справа на лево.
Начальное значение 335. Последний узел равен 1, значит мы вычитаем 1. Получаем 334.
Следующая команда ‘’припиши слева b.” У числа 334 слева стоит цифра 3. Можно решать до конца, но мы уже видим, что b =3.
Записываем значение в ответ.
Тип 3

Данную задачу также можно решить таблицей, но если кто-то может сразу использовать команды, подставим операции сразу вместо номеров команд.
Начальное значение равно 3, значит, (3+5+5+5)*b+5=77; 18*b+5=77 (решаем линейное уравнение)
18b=72 (:18) ; b=4
Записываем ответ.
Тип 4

Не всегда использование команд приводит к решению линейных уравнений. Поэтому рассмотрим ситуацию, когда приходится решать квадратное уравнение.
Мы также можем использовать таблицу для решения задачи. Это позволит избежать ошибок с потерями команд и скобок.
Но мы попробуем решить напрямую, используя наши команды.
Начальное значение равно 2. Мы видим подряд 4 Единцы. b+b+b+b=4*b . Прибавив начальное значение, получаем 4*b+2. Команда 2 возводит полученное выражение в квадрат. Получаем: (4*b+2)2. Приравниваем к конечному значению и получим уравнение:
(4*b+2)2=100
Воспользуемся формулой сокращенного умножения (квадрат суммы: (a+b)2=a2+2*a*b+b2)
4+16*b+16*b2=100
пересём слагаемое без переменной с противоположным знаком в правую часть
16*b+16*b2=100-4; 16*b+16*b2=96
В левой части вынесем общий множитель за скобку
16(b2+b)=96 (:16)
b2+b=6; b2+b-6=0
Мы получили квадратное уравнение приведенного вида с коэффициентами a=1 b=1 c=-6
Найдем дискриминант: D=b2-4*а*с=12-4*1*(-6) =1+24=25 0, значит уравнение имеет 2 различных действительных корня.
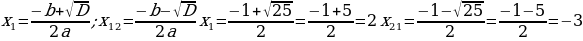
Согласно условию, b – натуральное число, т.е. оно не отрицательное и не равно нулю. Отсюда, b=2.
Записываем ответ.
Есть задания, где без дополнительных преобразований получаем квадратное уравнение. В таких случаях сразу переходим у определению коэффициентов и нахождения дискриминанта.
Тип 5.

При вычитании и делении, выполняя команды, мы идем от большего числа к меньшему числу. Давайте на этот раз решим табличкой.
| Номер команды | Выражение |
| Начальное значение | 40 |
| 1 | 40-b |
| 1 | 40-b-b=40-2b |
| 2 | (40-2b)/3 |
| 2 | ((40-2b)/3)3=(40-2b)/9 |
| 1 | (40-2b)/9-b |
Получили уравнение с дробным коэффициентом
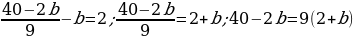
Раскроем скобки и перенесем в левую часть слагаемые с переменной, а в правую часть слагаемые без переменной и приведем подобные слагаемые.
40-2b=18+9b; -2b-9b=18-40 -11b=-22 :(-11)
b=2
Запишем ответ.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Разбор типовых задач по информатике на тему "Исполнители" (413.05 KB)
Разбор типовых задач по информатике на тему "Исполнители" (413.05 KB)
 0
0 4183
4183 19
19 Нравится
0
Нравится
0







