Получите свидетельство
Вход
Цели урока.
Способствовать формированию знаний о понятии равнобедренного треугольника, его элементов, свойств углов при основании равнобедренного треугольника, построение с помощью линейки, навыки применения полученных знаний при решении задач.
Развивать математическую грамотность, математическую речь, чертежные навыки, навыки анализа, логику мышления, навыки самоконтроля.
Воспитывать осознанное отношение к учебе.
Ход урока
Организационная и мотивационная части.
Показ рисунков: рисунки полей и гор, пчелиные соты.
Мир, в котором мы живем, наполнен геометрией улиц и домов, гор и полей, творениями природы и человека. Один мудрец сказал: “Высшее проявление духа – это разум. Высшее проявление ума – это геометрия. Клетка геометрии – это треугольник. Он так же неисчерпаем, как и Вселенная”.
Ну а мы с вами на уроках геометрии познакомились с треугольником.
Какая фигура называется треугольником? (Учащиеся дают определение треугольника).
На уроках геометрии очень важно уметь смотреть и видеть, замечать и отмечать различные особенности геометрических фигур.
Кто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает.
Знакомый всем с детства треугольник таит в себе немало интересного и загадочного, тайны которого мы и начали раскрывать на уроках геометрии.
Сегодня мы продолжим изучать треугольники и совершим удивительное путешествие в город Треугольников.
Все в нашем городе – друзья
Дружнее не сыскать.
Мы треугольников семья,
Нас каждый должен знать.
Дома и жители в этом городе треугольной формы.
Ты на меня, ты на него
На всех нас посмотри.
У нас всего, у нас всего
У нас всего по три!
(В.Г. Житомирский, Л.Н. Шеврин)
О каких элементах треугольника говорится в этом детском стихотворении? (Три стороны, три угла, три вершины).
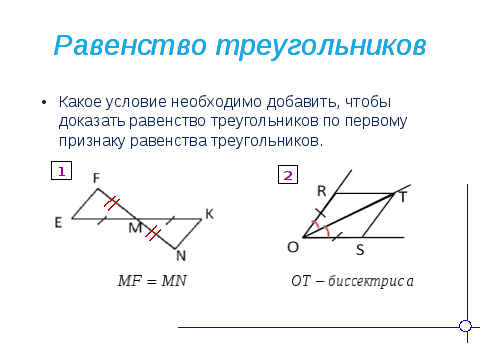
Работа в парах
На каждой парте лежат треугольники.
Разложите треугольники по углам (остроугольные, тупоугольные, прямоугольные). Заслушиваются ответы ребят.
А теперь внимательно посмотрите на их стороны и постарайтесь разложить их на группы по сторонам.
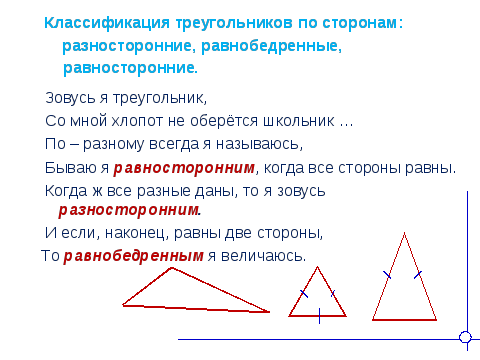
Проверяем, что получилось.
--Треугольники, у которых все стороны разные (разносторонние).
--Треугольники, у которых стороны равны (равносторонние).
--Треугольники, у которых две стороны равны (равнобедренные).
Отложите в сторону разносторонние треугольники, а о равнобедренных треугольниках мы сегодня с вами и поговорим.
Изучение нового материала.
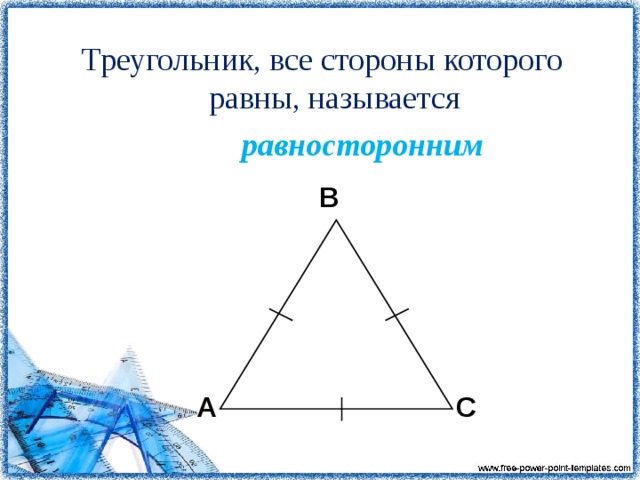
Тема урока: Равнобедренный треугольник.
Если так звучит тема, то какие цели поставим перед собой? (Повторить имеющиеся знания о треугольниках, дать определение равнобедренного треугольника, рассмотреть его элементы и свойства. Применение данных понятий при решении задач)
А
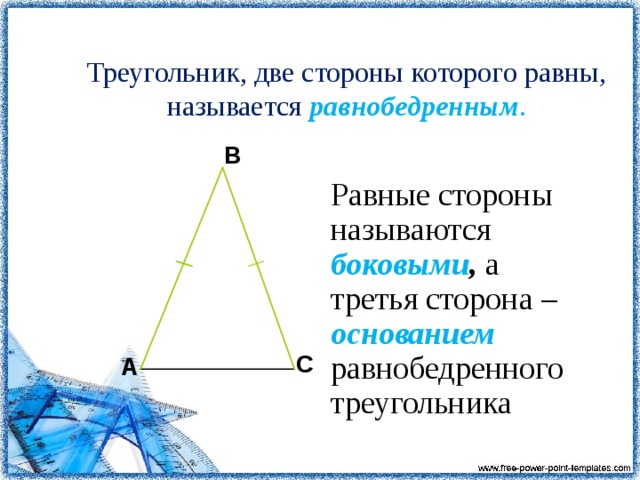
Определение 1: треугольник называется
равнобедренным, если у него
две стороны равны.
Равные стороны называются
боковыми сторонами, а третья
В С сторона называется основанием
треугольника. 
А
Определение 2: Треугольник называется
равносторонним, если у него
все стороны равны.
В С
Задание1: На треугольниках, которые лежат на партах подписать основания и боковые стороны.
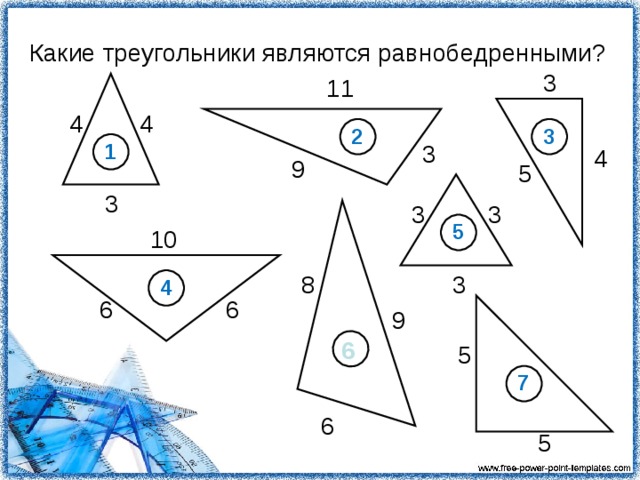
Задание 2: Какие из данных треугольников являются равнобедренными, почему?
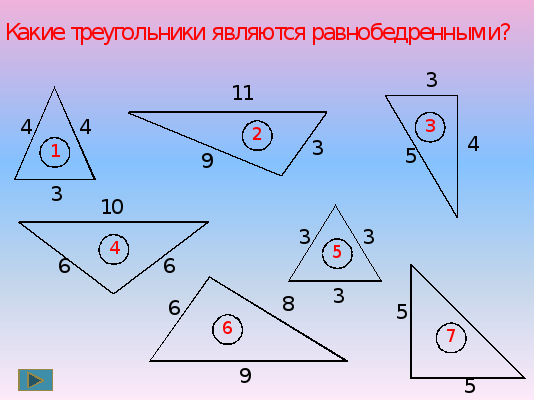
Является ли равносторонний треугольник – равнобедренным? (да)
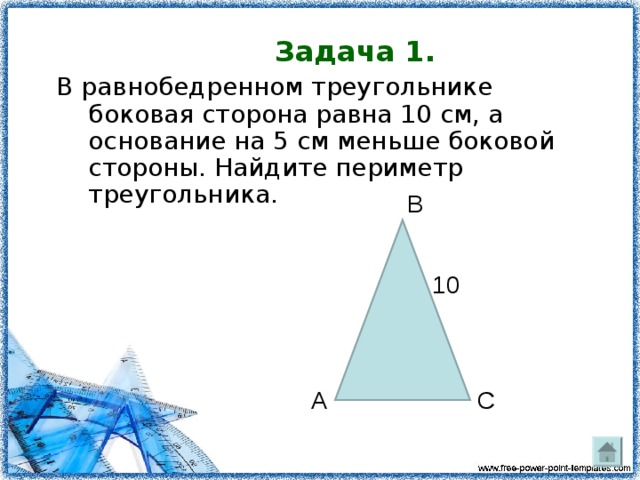
Задача: 1) в равнобедренном треугольнике боковая
А сторона равна 10 см, а основание на 5см
меньше боковой стороны. Найти периметр треугольника.
Ответ: 25см.
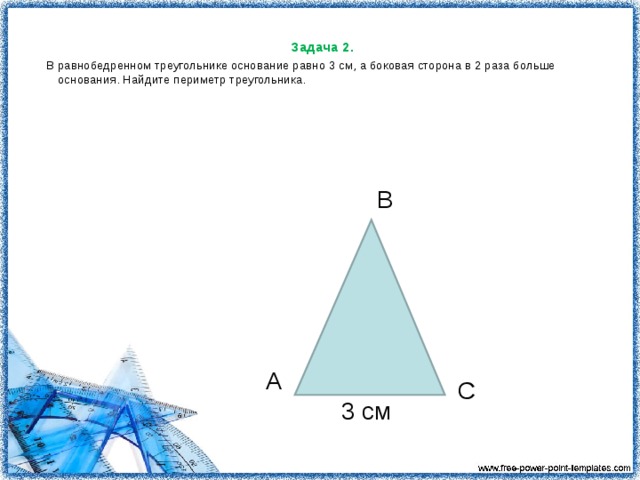
Задача: 2) в равнобедренном треугольнике основание
равно 3см, а боковая сторона в 2 раза больше основания. Найти периметр треугольника.
В С
Ответ: 15 см.
Задача: 3) основание в равнобедренном треугольнике в 2 раза
больше боковой стороны, а периметр равен 29 см.
Найдите стороны треугольника. Сделайте чертеж.
Запишите данные к задаче.
Задача решается на доске. Учитель показывает оформление задачи.
Практическая работа.
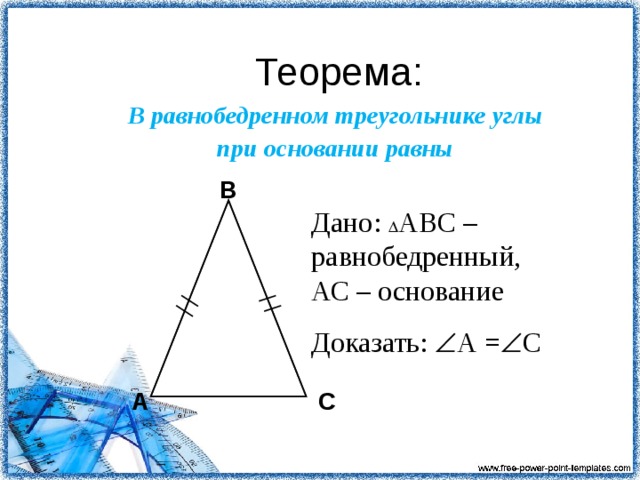
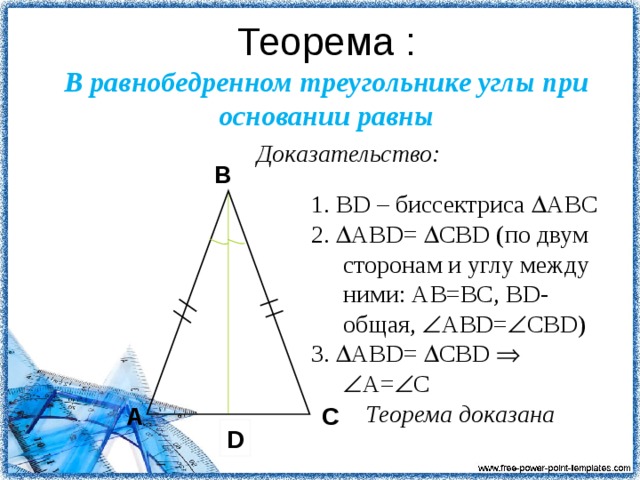
Посмотрите на равнобедренный треугольник, что можно сказать про его углы? ( они равны)( наложением)
Свойство равнобедренного треугольника.
Физкультминутка
Закрепление. Решение задач
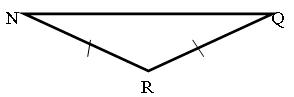
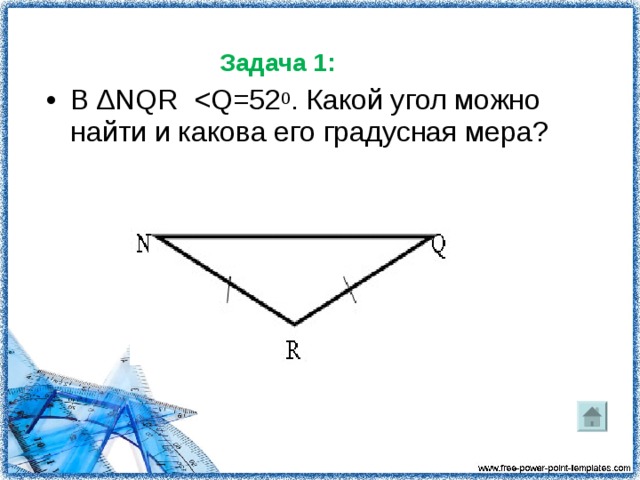
Задача 1:
В ∆NQR Q=520. Какой угол можно найти и какова его градусная мера?
Задача 2:
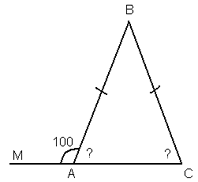
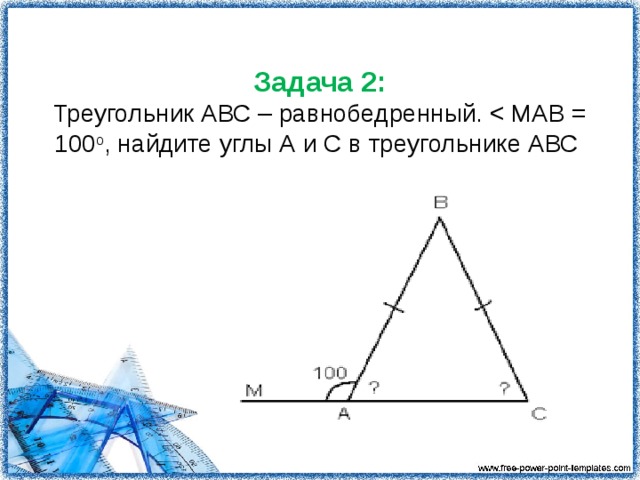
Треугольник АВС – равнобедренный 
МАВ = 100о, найдите А и С в треугольнике АВС
Равнобедренный треугольник в древности.
Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которой человек узнал ещё в глубокой древности. Например, то, что в равнобедренном треугольнике углы при основании равны, было известно ещё древним вавилонянам 4000 лет назад. Равнобедренный треугольник обладает ещё рядом геометрических свойств, которые всегда имели широкое применение в практической жизни.
Практическое применение равнобедренных треугольников.
В разных странах строят дома с разными крышами: у одних домов крыши остроугольные, а у других – тупоугольные. (Все зависит от погодных условий. Если стропила крыши образуют угол тупой, ближе к развернутому, то зимой на ней может скопиться столько снегу, что крыша может не выдержать. Поэтому, там, где зимой выпадает много снега, крышу делают с острым углом: снег на ней не будет задерживаться. Ну, а там, где очень тепло, дом можно строить и с плоской крышей)
Домашняя работа: п. 18, теорема, № 108, № 112
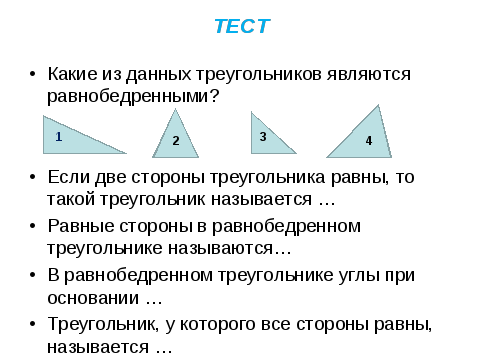
Ответы к тесту:
1) 2,3
2) Рвнобедренным.
3) боковыми
4) равны
5) равносторонним
Работы учащиеся проверяют сами и ставят оценку.
Итог урока:
Рефлексия.
Равнобедренный треугольник (24.62 MB)
0
1645
40
Нравится
0
