Равнобедренный треугольник и его свойства

Предмет: геометрия (7 класс)

Тема: Медианы, Биссектрисы и Высоты треугольника.,

Свойства равнобедренного треугольника

Подготовила материал: Учитель по математике, МБОУ СШ № 30 города Дзержинск: Кобякова Анна Викторовна

Общие понятия: Медиана, Биссектриса и Высота (треугольника)

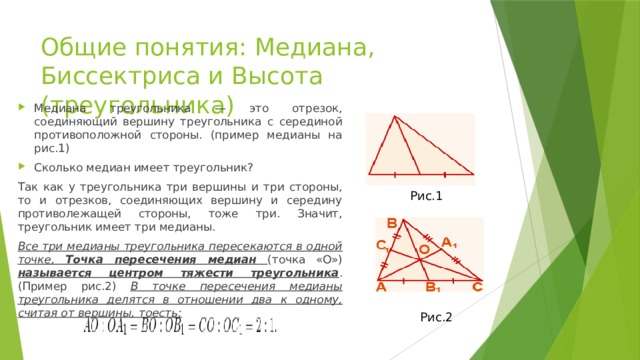
• Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. (пример медианы на рис.1)
• Сколько медиан имеет треугольник?

Так как у треугольника три вершины и три стороны, то и отрезков, соединяющих вершину и середину противолежащей стороны, тоже три. Значит, треугольник имеет три медианы.

Все три медианы треугольника пересекаются в одной точке, Точка пересечения медиан (точка «О») называется центром тяжести треугольника . (Пример рис.2) В точке пересечения медианы треугольника делятся в отношении два к одному, считая от вершины, тоесть:

Рис.1

Рис.2

Общие понятия: Медиана, Биссектриса и Высота (треугольника)

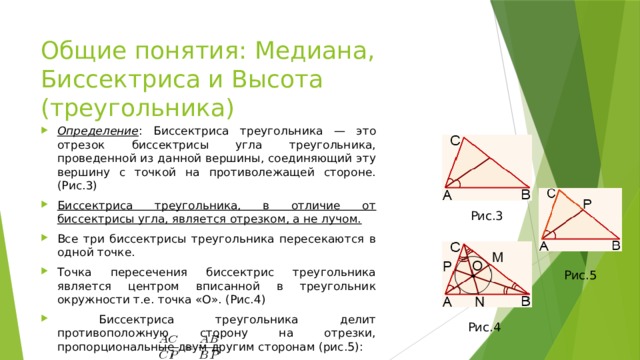
• Определение : Биссектриса треугольника — это отрезок биссектрисы угла треугольника, проведенной из данной вершины, соединяющий эту вершину с точкой на противолежащей стороне. (Рис.3)
• Биссектриса треугольника, в отличие от биссектрисы угла, является отрезком, а не лучом.
• Все три биссектрисы треугольника пересекаются в одной точке.
• Точка пересечения биссектрис треугольника является центром вписанной в треугольник окружности т.е. точка «О». (Рис.4)
• Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам (рис.5):

Рис.3

Рис.5

Рис.4

Общие понятия: Медиана, Биссектриса и Высота (треугольника)

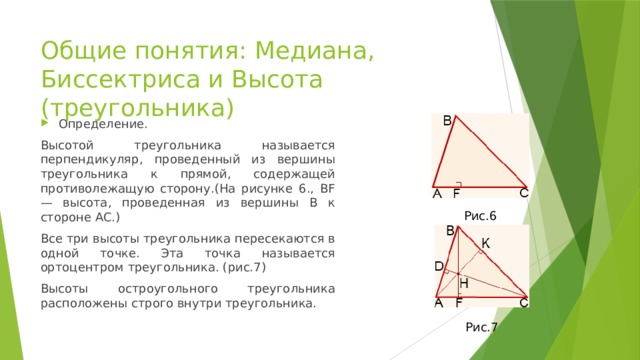
• Определение.

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.(На рисунке 6., BF — высота, проведенная из вершины B к стороне AC.)

Все три высоты треугольника пересекаются в одной точке. Эта точка называется ортоцентром треугольника. (рис.7)

Высоты остроугольного треугольника расположены строго внутри треугольника.

Рис.6

Рис.7

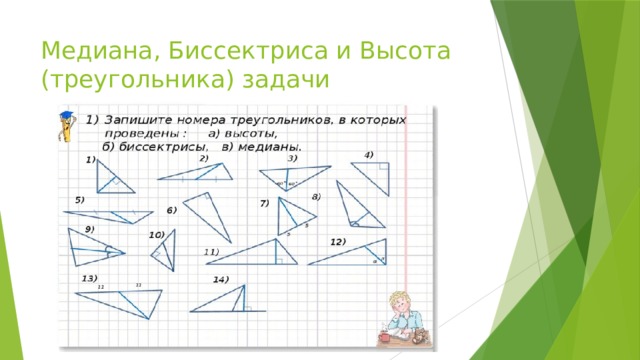
Медиана, Биссектриса и Высота (треугольника) задачи

Понятие «Равнобедренный треугольник»

• Что такое равнобедренный треугольник?

Рассмотрим определение равнобедренного треугольника и выясним, как называются его стороны и углы.

Определение: Равнобедренный треугольник — это треугольник, в котором две стороны равны. Эти равные стороны называются боковыми, а третья сторона называется основанием равнобедренного треугольника. Вершина равнобедренного треугольника — это та вершина, которая лежит напротив основания. Угол, лежащий напротив основания — угол при вершине равнобедренного треугольника. Два другие угла — углы при основании равнобедренного треугольника.

На рис.8 представлен равнобедренный АВС где «А»-вершина, «ВС»-основание, соответственно угол «А» является углом при вершине, а углы «В» и «С» углы при основании

Рис.8

Свойства равнобедренного треугольника

• 1) В равнобедренном треугольнике углы при основании равны.
• 2) В равнобедренном треугольнике: 1)медиана,2)биссектриса,3)и высота, проведенные к основанию, совпадают.
• 3) В равнобедренном треугольнике

— биссектрисы, проведенные из вершин при основании, равны;

— высоты, проведенные из вершин при основании, равны;

— медианы, проведенные из вершин при основании, равны.

Задачи по равнобедренному треугольнику

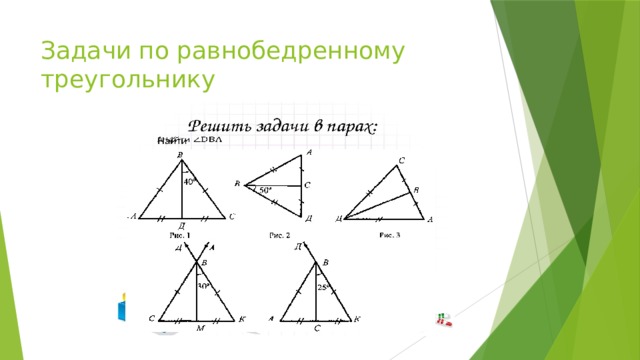
Задачи по равнобедренному треугольнику

Задачи по равнобедренному треугольнику

Ссылки

• http://www.treugolniki.ru/svojstva-ravnobedrennogo-treugolnika /
• Учебник А.Атанасяна «Геометрия 7-8-9 Класс» стр.33-35
• Педагогическое сообщество «Урок.РФ.»// https :// урок.рф /