Автономная некоммерческая организация дополнительного профессионального образования
«Уральский институт повышения квалификации и переподготовки»
Программа профессиональной переподготовки:
«Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Дисциплина: математика
Практическое задание 2, модуль 2
Выполнил:
слушатель Спирина А. В.
Преподаватель:
к.п.н. Гладнева С. Г.
Уральский Институт Повышения Квалификации и Переподготовки – 2017
Практическое задание 2
Цели:
Знать:
Требования Федерального государственного образовательного стандарта основного общего образования и Федерального государственного образовательного стандарта среднего (полного) общего образования к содержанию математического образования.
Научные и методические основы школьного курса математики, принципы построения программ по математике для основного и среднего (полного) образования и реализующих программы учебников.
Типологию уроков математики и структурные компоненты уроков различных типов.
Особенности организации уроков математики с использованием инновационных технологий.
Задачи и пути развития математической речи учащихся основной и средней (полной) школы.
Уметь:
Разбираться в содержании и требованиях программ по математике, в содержании и методическом аппарате школьных учебников, в структуре и замысле пособий для учащихся, реализовывать требования программ, методические возможности учебников и учебных пособий.
Самостоятельно планировать изучение разделов и тем школьного курса математики, циклы уроков и отдельные уроки, в том числе с использованием инновационных технологий.
Изучать уровень математических знаний и умений школьников, оценивать результаты математического образования.
Самостоятельно подбирать и правильно использовать учебный материал по математике, обоснованно выбирать методы и методические приёмы.
Устанавливать межпредметные связи между методикой преподавания математики, педагогикой, психологией, математикой.
Изучать передовой опыт учителей, элементарно оценивать его.
Задание 1. Выберите одно какое-либо конкретное понятие (или одну тему, или один раздел/модуль и проч.), изучаемое(ую, ый) в 5-6, 7-9, 10-11 классах в одном каком-либо УМК.
Сравните содержание и методику изучения этого понятий (этого раздела/модуля, этой темы) на разных этапах математического образования.
Оформите ответ следующим образом:
УМК:
Изучаемое понятие (изучаемая тема/изучаемый раздел/модуль):
Тема: «Расширение числовых множеств при изучении чисел в курсе средней школы».
| Цели изучения | Содержание работы | Методика работы (общая характеристика) | Конкретные примеры заданий | |||
| 5-6 классы | ||||||
| Систематизировать и обобщить сведения о натуральных числах, полученные в начальной школе. Закрепить и развить навыки сложения и вычитания натуральных чисел; выработать умения умножать и навыки арифметических делить десятичные дроби, выполнять задания на все действия действий с натуральными числами; познакомить учащихся с понятием дроби; завершить изучение натуральных чисел, подготовить основу для освоения действий с обыкновенными дробями; выработать умения читать, записывать, сравнивать, округлять десятичные дроби, выполнять сложение и вычитание десятичных дробей; с натуральными числами и десятичными дробями; расширить представления учащихся о числе путём введения отрицательных чисел;– выработать прочные навыки сложения и вычитания положительных и отрицательных чисел;– выработать прочные навыки арифметических действий с положительными и отрицательными числами.
| Сравнение рациональных чисел. Действия с рациональными числами. Конечные и бесконечные десятичные дроби. Представление рационального числа в виде десятичной дроби.
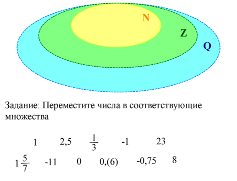
| Первое множество, с которым познакомились - это множество натуральных чисел N={1,2,3,…,n} В этом множестве выполнимы действия сложения и умножения, т.е. всегда разрешимы уравнения x-m=n →x=m+n и →x=m*n (1) Однако вычитание уже не всегда выполнимо, т.е. уравнение x+m=n (2) не всегда разрешимо, как , например, уравнение x+5=3. Для того, чтобы сделать разрешимым это уравнение множество N было расширено. Было введено множество Z целых чисел Z={0,1,-1,2,-2,…}, Содержащее в себе как часть множество N. В этом множестве уже вычитание всегда возможно, т.е. разрешимы не только уравнения (1), но и (2). Однако, в этом множестве не всегда выполнимо действие деления, т.е. уравнение x*m=n (3) не всегда разрешимо, как, например, уравнение 3*x=5. Для того, чтобы уравнение (3) было всегда разрешимым, было сделано новое расширение числового множества. Было введено множество Q рациональных чисел. Q = { : где m Z, n }; Z } В этом множестве выполнимо действие деления на число, отличное от нуля, т.е. разрешимо уравнение (3). Таким образом, во множестве Q выполнимы все четыре арифметических действия. Оно, однако, не полностью нас удовлетворяет: в нём не всегда выполнимо действие извлечение из корня. |
| |||
| 7-9 классы | ||||||
| Дать представление о рациональных и иррациональных числах, ввести понятие стандартного вида числа, сформировать умение вычислять погрешности.
| Понятие иррационального числа. Распознавание иррациональных чисел. Действия с иррациональными числами. Свойства действий с иррациональными числами. Сравнение иррациональных чисел. Множество действительных чисел. Представления о расширениях числовых множеств.
| Дальнейшим расширением множества Q является введение множества R вещественных чисел, состоящее рациональных и иррациональных чисел, т.е. . В этом множестве помимо арифметических действий выполнимо, извлечение корня любой натуральной степени из неотрицательного числа. Но действие извлечения корня любой степени из любого числа остаётся неразрешимым. Для того, чтобы сделать разрешимым извлечение корня всегда всегда, требуется ещё большее расширение числовой системы, введение нового числового множества K, содержащее в себе R как часть, в котором было бы выполнимо действие извлечения корня любой степени из любого числа.
| Пример 1. Извлечь корень из дроби,
Пример 2. Исключить иррациональность в знаменателе дроби Пример 3. Докажите, что а) число √7; б) число lg 80; в) число √2 + 3√3; является иррациональным. Решение: а) Допустим, что число √7 рациональное. Тогда, существуют такие взаимно простые p и q, что √7 = p/q, откуда получаем p2 = 7q2. Так как p и q взаимно простые, то p2, а значит и p делится на 7. Тогда р = 7k, где k – некоторое натуральное число. Отсюда q2 = 7k2 = pk, что противоречит тому, что p и q взаимно просты. Итак, предположение ложно, значит, число √7 иррациональное. б) Допустим, что число lg 80 рациональное. Тогда существуют такие натуральные p и q, что lg 80 = p/q, или 10p = 80q, откуда получаем 2p–4q = 5q–p. Учитывая, что числа 2 и 5 взаимно простые, получаем, что последнее равенство возможно только при p–4q = 0 и q–p = 0. Откуда p = q = 0, что невозможно, так как p и q выбраны натуральными. Итак, предположение ложно, значит, число lg 80 иррациональное. в) Обозначим данное число через х. Тогда (х – √2)3 = 3, или х3 + 6х – 3 = √2·(3х2 + 2). После возведения этого уравнения в квадрат получаем, что х должен удовлетворять уравнению х6 – 6х4 – 6х3 + 12х2 – 36х + 1 = 0. Его рациональными корнями могут быть только числа 1 и –1. Проверка же показывает, что 1 и –1 не являются корнями. Итак, данное число √2 + 3√3 является иррациональным.
| |||
| 10-11 классы | ||||||
| Увеличение числа допустимых операций над числами. | Расширение множества вещественных чисел. Понятие комплексного числа. Арифметические операции для комплексных чисел. Геометрическое представление комплексных чисел. Комплексная плоскость. Модуль и аргумент комплексного числа. Тригонометрическаяформа комплексного числа. Операции с комплексными числами в тригонометрической форме
| Необходимость в комплексных числах появилась при решении квадратных уравнений для случая D здесь D – дискриминант квадратного уравнения) Комплексные числа получаются из действительных чисел Число где сохраняются все арифметические операции и их свойства | Пример . Найдем все корни степени 3 из единицы. Для этого найдем все корни уравнения z3 = 1, корни будем искать в показательной форме. Последний тип задач включается в себя огромное множество задач и нет общих методов их решения. Приведем простой пример такой задачи: Найти сумму sin(x) + sin(2x) + sin(2x) + … + sin(nx). Хоть в формулировке этой задачи и не идет речь о комплексных числах, но с их помощью ее можно легко решить. Для ее решения используются следующие представления: | |||

 Получите свидетельство
Получите свидетельство Вход
Вход






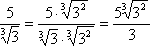 .
. добавлением нового числа
добавлением нового числа 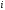 , обладающего свойством
, обладающего свойством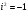 .
.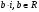 , а во-вторых, и все числа вида
, а во-вторых, и все числа вида 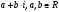 . Множество всех таких чисел называется множеством комплексных чисел (комплексной плоскостью) и обозначается
. Множество всех таких чисел называется множеством комплексных чисел (комплексной плоскостью) и обозначается 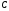 ,
,








 Расширение числовых множеств при изучении чисел в курсе средней школы (273.43 KB)
Расширение числовых множеств при изучении чисел в курсе средней школы (273.43 KB)
 0
0 1488
1488 104
104 Нравится
0
Нравится
0


