Программа спецкурса для 9 класса «Избранные вопросы математики»
составитель
Половинкина Татьяна Николаевна
учитель математики
МОУ Игнатовской СОШ Майнского района
2014
Пояснительная записка
Настоящая программа написана на основании следующих нормативных документов:
Федерального компонента государственного стандарта основного общего образования утверждённого приказом Министерства образования РФ от 05.03.2004, № 1089;
Федерального базисного учебного плана для ОУ РФ утверждённого приказом Министерства образования РФ от 09.03.2004, № 1312;
Программы основного общего образования. Математика.
Так же данная программа написана с использованием научно-методических и методических рекомендаций:
Методических рекомендаций по организации предпрофильной подготовки и профильного обучения. Математика. /автор-составитель Ф.С. Мухаметзянова.; Под редакцией Т.Ф. Есенковой, В.В. Зарубной. – Ульяновск; УИПКПРО, 2005
Цели обучения математике, а общеобразовательной школе определяются её ролью в развитии общества в целом и формировании личности каждого отдельного человека.
Исторически сложились две стороны назначения математического образования: практическая, связанная с созданием и применением инструментария, необходимого человеку в его продуктивной деятельности, и духовная, связанная с мышлением человека, с овладением определённым методом познания и преобразования мира математическим методом
Практическая полезность математики обусловлена тем, что её предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения – от простейших усваиваемых в непосредственном опыте людей, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие научных знаний, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчёты, пользоваться общеупотребительной вычислительной техникой, находить в справочниках и применять нужные формулы, владеть практическими приёмами геометрических измерений и построений, читать информацию, представленную виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни становится непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, всё больше специальностей, требующих высокого уровня образования, связано с непосредственным применением математики (экономика, бизнес, физика, химия, техника, информатика, биология, психология и многое другое). Таким образом, расширяется круг школьников, для которых математика становится профессионально значимым предметом.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определённых умственных навыках. В процессе математической деятельности в арсенал приёмов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления, воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач – основной учебной деятельности на уроках математики – развиваются творческая и прикладная стороны мышления.
Использование в математике наряду с естественным нескольких математических языков даёт возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносить свой склад в формирование общей культуры человека. Необходимым компонентом общей культуры в её современном толковании является общее знакомство с методами познания действительности, что включает понимание диалектической взаимосвязи математики и действительности, представление о предмете и методе математики, его отличиях от методов естественных и гуманитарных наук, об особенностях применения математики для решения прикладных и научных задач. Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии. Изучение математики развивает воображение, пространственные представления. История развития математического знания даёт возможность пополнить запасы историко-научных знаний школьников, сформировать у них представление о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, судьбами великих людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
Роль математической подготовки в общем образовании современного человека ставит следующие цели обучения математике в школе:
Овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
Интеллектуальное развитие учащихся формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
Формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
Формирование представлений о математике как части общечеловеческой культуры понимания значимости математики для общественного прогресса.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому человеку, достаточных для изучения смежных дисциплин и продолжение образования.
Наряду с решением основной задачи расширенное и углубленное изучение математики предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, существенным образом связанные с математикой, подготовку к дальнейшему обучению
Курс направлен на восполнение недостающих знаний, отработку приемов решения заданий различных типов и уровней сложности вне зависимости от формулировки. Курс составлен на основе Обязательного минимума содержания основных образовательных программ и Требований к уровню подготовки выпускников основной школы
Программа предусматривает продолжительность образовательного процесса 34 учебных недели в течение учебного года, 1 занятие в неделю.
Цель данного спецкурса: систематизация знаний и умений за курс основной школы, повышение уровня математической культуры.
Задачи: сформировать у учащихся умение определять вид задания, представлять способ его решения; сформировать высокий уровень активности; развить интерес к математике; способствовать профориентации.
Курс состоит из пяти тем. Изучаемый материал примыкает к основному курсу, дополняя его историческими сведениями, сведениями важными в общеобразовательном или прикладном отношении, материалами занимательного характера и расширении теоретического материала. Данный курс поможет научить школьника технике работы с тестовыми заданиями
В ходе изучения материала данного курса целесообразно сочетать такие формы организации учебной работы, как практикумы по решению задач, лекции, беседа, тестирование, частично-поисковая деятельность. Развитию математического интереса способствуют математические игры (дидактическая, ролевая), викторины, головоломки. Необходимо использовать элементы исследовательской деятельности. После рассмотрения полного курса учащиеся должны иметь следующие результаты обучения:
уметь определять тип задания, знать алгоритм решения;
уметь применять полученные математические знания в решении жизненных задач;
уметь использовать дополнительную математическую литературу с целью углубления материала основного курса, расширения кругозора и формирования мировоззрения, раскрытия прикладных аспектов математики.
В результате освоения содержания программы учащийся получает возможность совершенствовать и расширить круг умений, навыков и способов деятельности:
Познавательная деятельность.
Умение самостоятельно и мотивированно организовать свою познавательную деятельность. Создание идеальных и реальных моделей объектов, процессов.
Информационно-коммуникативная деятельность.
Поиск и извлечение нужной информации по заданной теме в источниках различного типа. Умение развернуто обосновать суждение, давать определения, приводить доказательства.
Рефлексивная деятельность.
Владение навыками организации и участие в коллективной деятельности: постановка общей цели и определение средств её достижения, конструктивное восприятие иных мнений и идей, учет индивидуальности партнеров по деятельности, объективное определение своего вклада в общий результат.
Формирование ключевых компетентностей:
готовность к самообразованию;
готовность к использованию информационных ресурсов;
готовность к социальному взаимодействию;
коммуникативная компетентность.
Инструментарием для оценивания результатов могут быть: тестирование, творческие работы.
Структура программы состоит из двух блоков теоретического и практического. Содержание курса состоит из 9 математических модулей. Основное содержание предполагает два уровня базовый и повышенный.
В результате работы по программе учащиеся должны знать:
-методы проверки правильности решения заданий
-методы решения различных видов уравнений и неравенств
-основные приемы текстовых задач, а также проверки правильности их решения
-методы нахождения статистических характеристик
-методы решения геометрических задач
Должны уметь :
-проводить преобразования в степенных и дробно-рациональных выражениях
-применять свойства арифметических и геометрических прогрессий
-решать различные текстовые задачи
-находить вероятности случайных событий в простейших случаях
-использовать приобретенные знания в различных жизненных ситуациях, практической деятельности
-уметь распознавать геометрические фигуры, различать взаимное расположение, изображать геометрические фигуры, выполнять чертежи по условию задачи
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
- овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
- формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
- воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Планируемые результаты обучения:
Сформированная база знаний в области алгебры, геометрии.
Устойчивые навыки определения типа задачи и оптимального способа ее решения независимо от формулировки задания
Умение работать с задачами в нетипичной постановке условий.
Умение работать с тестовыми заданиями.
Умение правильно распределять время, отведенное на выполнение заданий.
Учебный план
| Название модуля | Кол-во часов | Теория | Практика |
| 1.Числа и числовые выражения, проценты | 3 | 1 | 1 |
| 2.Буквенные выражения | 2 |
| 2 |
| 3.Преобразование выражений. Формулы сокращенного умножения. Рациональные дроби | 2 |
| 2 |
| 4. Уравнения и неравенства. | 4 | 1 | 2 |
| 5.Прогрессии: арифметическая и геометрическая. | 2 | 1 | 1 |
| 6. Функции и графики | 3 | 1 | 2 |
| 7.Текстовые задачи. | 5 |
| 2 |
| 8.Элементы комбинаторики и теории вероятностей. | 2 | 1 | 2 |
| 9. Геометрические задачи. | 5 | 1 | 2 |
| 10. Решение задач | 6 |
| 6 |
| Итого: | 34 | 6 | 28 |
Содержание учебных модулей
1.Числа и числовые выражения, проценты
Натуральные числа. Арифметические действия с натуральными числами. Свойства арифметических действий. Делимость натуральных чисел. Делители и кратные числа. Признаки делимости на 2,3,5,9,10.Деление с остатком. Простые числа. Разложение натурального числа на простые множители.
Нахождение НОД и НОК. Обыкновенные дроби. Действия с обыкновенными дробями. Десятичные дроби, действия с десятичными дробями.
Применение свойств для упрощения выражений Тождественно равные выражения. Проценты. Нахождение процента от числа и числа по его проценту.
2.Буквенные выражения
Выражения с переменными. Тождественные преобразования выражений с переменными. Значение выражений при известных числовых данных переменных.
3.Преобразование выражений. Формулы сокращенного умножения. Рациональные дроби
Одночлены и многочлены. Стандартный вид одночлена, многочлена. Коэффициент одночлена. Степень одночлена, многочлена. Действия с одночленами и многочленами. Формулы сокращенного умножения. Способы разложения многочлена на множители. Рациональные дроби и их свойства. Допустимые значения переменных. Тождество, тождественные преобразования рациональных дробей. Степень с целым показателем и их свойства. Корень n-ой степени, степень с рациональным показателем и их свойства.
4. Уравнения и неравенства
Линейные уравнения с одной переменной. Корень уравнения. Равносильные уравнения. Системы линейных уравнений. Методы их решения. Квадратные уравнения. Теорема Виета. Неравенства с одной переменной. Система неравенств. Методы решения систем неравенств.
5.Прогрессии: арифметическая и геометрическая.
Числовые последовательности. Арифметическая прогрессия. Разность арифметической прогрессии. Формула n-го члена и суммы n-первых членов арифметической прогрессии. Геометрическая прогрессия, знаменатель геометрической прогрессии. Формула n-го члена и суммы n-первых членов геометрической прогрессии. Сумма бесконечной геометрической прогрессии.
6. Функции и графики.
Понятие функции. Функция и аргумент Область определения и область значений функции. График и нули функции. Функция, возрастающая и убывающая на отрезке. Линейная функция и ее свойства. Обратно-пропорциональная функция ее свойства и график. Квадратичная функция ее свойства и график. Степенная функция. Свойства четной и нечетной степенной функций. Чтение графиков функций.
7. Текстовые задачи.
Задачи на движение и способы их решения. Задачи на вычисление объема и способы их решения. Задачи на процентное содержание веществ в смесях, сплавах и растворах и способы их решения.
8.Элементы статистики и теории вероятностей.
Среднее арифметическое, размах мода. Медиана как статистическая характеристика Методы решения комбинаторных задач: перебор возможных ситуаций, дерево вариантов, правило умножения. Перестановки, размещение сочетания. Вероятность случайного события. Сложение и умножение вероятностей.
9.Треугольники
Равнобедренный и равносторонний треугольники. Признаки равенства и подобия треугольников. Высота, медиана, средняя линия треугольника.
Решение треугольника. Сумма углов треугольника. Свойства прямоугольных треугольников Теорема Пифагора. Теорема синусов и косинусов. Неравенство треугольников. Площадь треугольников.
Литература
1.Государственная итоговая аттестация выпускников 9 классов в новой форме. Алгебра.2010/ФИПИ.-М.:Интеллект-Центр.2010.-128с
2. Математика/Геометрия/. Подготовка к ГИА.-Саратов:Лицей,2012.-64с
3.ГИА2013.Математика:типовыеэкзаменационныематериалы/подредА.Л.Семенова,И.В.Ященко.-М.:Издательство, ,Национальное образование,, , 2013. 192с.-/ГИА-2013.ФИПИ-школе/
4.Математика.9 класс. Тематические тесты для подготовки к ГИА-9.Алгебра,геометрия, теория вероятностей и статистика: учебно-методическое пособие/под ред. Ф.Ф.Лысенко, С.Ю. Кулабухова. -Ростов н/Д: Легион-М,2011.-288с.-/ГИА-9/
Перечень сайтов
1.http://www.prosv.ru – сайт издательства, Просвещение, /рубрика,,Математика,,/
2.http://www.drofa.ru-сайт издательства, ,Дрофа,, /рубрика,,Математика,,/
3.http://www.legion.ru-сайт издательства, ,Легион,,
4.http://www. fipi. ru-портал информационной поддержки мониторинга качества образования здесь содержится Федеральный банк тестовых заданий.
5.http://zadachi.mccme.ru-Задачи по геометрии :информационно-поисковая система.
6.http://www.intelekt centre.ru-Сайт издательства, , Интеллект центр,,
7.http://www.edu.ru-Центральный образовательный портал, содержит нормативные документы Министерства, стандарты и информацию о проведении эксперимента.
Календарно-тематическое планирование
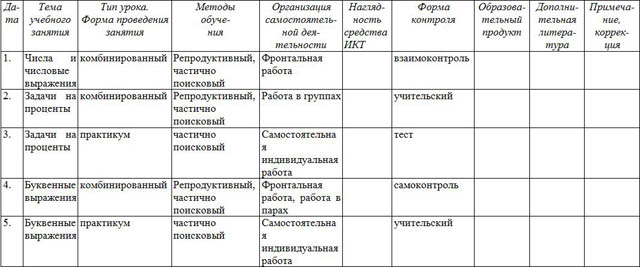
| Да- та | Тема учебного занятия | Тип урока. Форма проведения занятия | Методы обуче- ния | Организация самостоятельной деятельности | Нагляд- ность средства ИКТ | Форма контроля | Образова-тельный продукт | Дополнительная литература | При-мечание, коррек- ция |
-
| Числа и числовые выражения | комбинированный | Репродуктивный, частично поисковый | Фронтальная работа |
| взаимоконтроль |
|
|
|
-
| Задачи на проценты | комбинированный | Репродуктивный, частично поисковый | Работа в группах |
| учительский |
|
|
|
-
| Задачи на проценты | практикум | частично поисковый | Самостоятельная индивидуальная работа |
| тест |
|
|
|
-
| Буквенные выражения | комбинированный | Репродуктивный, частично поисковый | Фронтальная работа, работа в парах |
| самоконтроль |
|
|
|
-
| Буквенные выражения | практикум | частично поисковый | Самостоятельная индивидуальная работа |
| учительский |
|
|
|
-
| Преобразование выражений. Формулы сокращенного умножения | комбинированный | Репродуктивный, частично поисковый | Фронтальная работа, работа в парах |
| учительский |
|
|
|
-
| Преобразование выражений. Рациональные дроби | комбинированный | Репродуктивный, частично поисковый | Самостоятельная индивидуальная работа |
| тест |
|
|
|
-
| Уравнения. | комбинированный | Репродуктивный, частично поисковый | Фронтальная работа, работа в парах |
| самоконтроль |
|
|
|
-
| Неравенства | комбинированный | Репродуктивный, частично поисковый | Фронтальная работа, работа в парах |
| самоконтроль |
|
|
|
-
| Уравнения и неравенства. | практикум | частично поисковый | Самостоятельная дифференцированная работа |
| тест |
|
|
|
-
| Уравнения и неравенства. | практикум | частично поисковый | Самостоятельная индивидуальная работа |
| учительский |
|
|
|
-
| Прогрессии: арифметическая и геометрическая. | комбинированный | Репродуктивный, частично поисковый | Фронтальная работа, работа в парах |
| самоконтроль |
|
|
|
-
| Прогрессии: арифметическая и геометрическая. | практикум | частично поисковый | Самостоятельная индивидуальная работа |
| учительский |
|
|
|
-
| Функции и графики | комбинированный | Репродуктивный, частично поисковый | Фронтальная работа, работа в парах |
| самоконтроль |
|
|
|
-
| Функции и графики | практикум | частично поисковый | Работа в группах |
| тест |
|
|
|
-
| Функции и графики | практикум | частично поисковый | Самостоятельная индивидуальная работа |
| учительский |
|
|
|
-
| Текстовые задачи. | комбинированный | Репродуктивный, частично поисковый | Работа в парах |
| самоконтроль |
|
|
|
-
| Текстовые задачи. | практикум | частично поисковый | Работа в группах |
| взаимоконтроль |
|
|
|
-
| Текстовые задачи. | практикум | частично поисковый | Самостоятельная дифференцированная работа |
| взаимоконтроль |
|
|
|
-
| Текстовые задачи. | практикум | частично поисковый | Самостоятельная дифференцированная работа |
| тест |
|
|
|
-
| Текстовые задачи. | практикум | частично поисковый | Самостоятельная индивидуальная работа |
| учительский |
|
|
|
-
| Элементы комбинаторики и теории вероятностей | комбинированный | Репродуктивный, частично поисковый | Фронтальная работа, работа в парах |
| самоконтроль |
|
|
|
-
| Элементы комбинаторики и теории вероятностей | практикум | частично поисковый | Самостоятельная индивидуальная работа |
| учительский |
|
|
|
-
| Геометрические задачи. | комбинированный | Репродуктивный, частично поисковый | Фронтальная работа, работа в парах |
| взаимоконтроль |
|
|
|
-
| Геометрические задачи. | комбинированный | Репродуктивный, частично поисковый | Фронтальная работа, работа в парах |
| самоконтроль |
|
|
|
-
| Геометрические задачи. | практикум | частично поисковый | Самостоятельная дифференцированная работа |
| самоконтроль |
|
|
|
-
| Геометрические задачи. | практикум | частично поисковый | Самостоятельная дифференцированная работа |
| тест |
|
|
|
-
| Геометрические задачи. | практикум | частично поисковый | Самостоятельная индивидуальная работа |
| учительский |
|
|
|
-
| Решение задач | практикум | частично поисковый | Самостоятельная индивидуальная работа |
| самоконтроль |
|
|
|
-
| Решение задач | практикум | частично поисковый | Самостоятельная дифференцированная работа |
| самоконтроль |
|
|
|
-
| Решение задач | практикум | частично поисковый | Самостоятельная индивидуальная работа |
| взаимоконтроль |
|
|
|
-
| Решение задач | практикум | частично поисковый | Самостоятельная индивидуальная работа |
| взаимоконтроль |
|
|
|
-
| Проверочная работа | контроль | частично поисковый | Самостоятельная дифференцированная работа |
| учительский |
|
|
|
-
| Проверочная работа | контроль | частично поисковый | Самостоятельная дифференцированная работа |
| учительский |
|
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа спецкурса по математике (9 класс) (0.18 MB)
Рабочая программа спецкурса по математике (9 класс) (0.18 MB)
 0
0 1602
1602 298
298 Нравится
0
Нравится
0






