муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа №23 Волчанского городского округа
СОГЛАСОВАНО ………………… УТВЕРЖДАЮ Руководитель ШМО ………………… директор МАОУ СОШ №23 …………………/ ……………………./ …………………… С.Г. Снигирева Протокол от ………………….. № … Приказ от ……………… № ………
Рабочая программа по учебному предмету математика (геометрия) общего образования 11 класс на 2014-2015 учебный год
Составитель: Тимошенко Галина Николаевна, учитель математики, I квалификационная категория
2014год.
Пояснительная записка
Уровень изучения учебного материала: базовый
Рабочая программа разработана на основе
- требований федерального компонента государственного образовательного стандарта общего образования;
- санитарно-эпидемиологических требований к условиям и организации обучения в ОУ(утверждены
постановлением Главного государственного санитарного врача РФ от 29.12.2010г. №189)
- учебного плана МАОУ СОШ №23 (федерального и регионального компонента, компонента ОУ);
- календарного учебного графика на текущий учебный год;
- образовательной программы МАОУ СОШ № 23 среднего общего образования;
- программой министерства образования РФ по геометрии 10-11 класс авторы: Л.С.Атанасян, В. Ф. Бутузов, С.Б. Кадомцев, Л.С.Киселева, Э. Г. Позняк. Составитель Т. А. Бурмистрова. – М.: Просвещение, 2010г
- требований к оснащению образовательного процесса.
Преподавание ведется по учебнику Геометрия 10-11 классы: / Л.С.Атанасян, В. Ф. Бутузов, С.Б. Кадомцев, Л.С.Киселева, Э. Г. Позняк. / М.: Просвещение, 2010
Количество часов по программе -70, в неделю - 2 часа.
При изучении курса математики на базовом уровне продолжается и получает развития содержательная линия «Геометрия». В рамках этой линии решаются следующие задачи: изучение свойств пространственных тел, формирование умения применять полученные знания для решения практических задач.
Изучение математики в старшей школе на базовом уровне направлено на достижение следующих целей; _
- систематическое изучение свойств геометрических тел в пространстве;
- дальнейшее развитие логического мышления учащихся.
- формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математике;
- развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
- овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
- воспитание средствами математики культуры личности: отношение к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Основные задачи курса:
-научить работать с книгой;
-базировать изучение курса стереометрии в сочетании наглядности и логической строгости;
-осуществлять индивидуальный подход к учащимся;
-сформировать устойчивый интерес к предмету;
-обеспечить прочное и сознательное овладение системой знаний и умений.
Общеучебные умения, навыки и способы деятельности.
В ходе освоения содержания геометрического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
- построения и исследования математических моделей для описания решений прикладных задач, задач из смежных дисциплин;
- выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
- самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт.
- проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
- самостоятельной и коллективной деятельности, включения своих результатов и результатов работы группы, соотнесения своего мнения с мнением других участников учебного коллектива и мнением авторитетны источников.
Межпредметные и межкурсовые связи:
При работе широко используются: физика – тема «Метод координат в пространстве», «Цилиндр, конус и шар»; химия - тема «Объёмы тел»
Формы организации учебного процесса: индивидуальные, групповые, индивидуально-групповые, фронтальные, классные и внеклассные.
Формы контроля: Самостоятельная работа, контрольная работа, наблюдение, зачёт, работа по карточке.
Виды организации учебного процесса: Самостоятельные работы, контрольные работы, зачёты, выставки.
Требования к уровню подготовки учащихся:
Требования к результатам обучения направлены на реализацию деятельностного, практикоориентированного и личностно ориентированного подходов; освоение учащимися интеллектуальной и практической деятельности; овладение знаниями и умениями, востребованными в повседневной жизни, позволяющими ориентироваться в окружающем мире, значимыми для сохранения окружающей среды и собственного здоровья.
В результате изучения геометрии на базовом уровне ученик должен: знать/понимать:
- существо понятия доказательства, примеры доказательств;
- существо понятия алгоритма; примеры алгоритмов;
- как используются формулы; примеры их применения для решения практических задач;
Уметь
- распознавать на чертежах и моделях пространственные формы; соотносить трёхмерные объекты с их описанием, изображениями;
- описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
- анализировать в простейших случаях взаимное расположение объектов в пространстве;
- изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
- строить простейшие сечения куба, призмы, пирамиды;
-решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин( длин, углов, площадей, объёмов);
- использовать при решении стереометрических задач планиметрические факты и методы;
- проводить доказательные рассуждения в ходе решения задач.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для :
-исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
- вычисления объёмов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Содержание тем учебного курса
Метод координат в пространстве.
Прямоугольная система координат в пространстве. Координаты вектора. Связь между координатами вектора и координатами точек. Простейшие задачи в координатах. Угол между векторами. Вычисление углов между прямыми и плоскостями. Центральная симметрия. Осевая симметрия. Зеркальная симметрия. Параллельный перенос.
Основные цели: формирование понятия вектора в пространстве, понятия координатных векторов, разложение произвольного вектора по координатным, навыки действий над векторами с заданными координатами, формирование понятия радиус-вектора, отработать понятие коллинеарных и компланарных векторов при решении задач, вывести формулы координат середины отрезка, длины вектора через его координаты и расстояния между двумя точками; показать примеры решения стереометрических задач координатно-векторным методом; ввести понятие угла между векторами и скалярного произведения в координатах; познакомить с понятием движения пространства и основными видами движений;
Знать:
- понятие прямоугольной системы координат в пространстве;
- понятие координат вектора в прямоугольной системе координат;
- понятие радиус-вектора произвольной точки пространства;
- формулы координат середины отрезка, длины вектора через его координаты, расстояние между двумя точками;
- понятие угла между векторами;
- понятие скалярного произведения векторов;
- формулу скалярного произведения в координатах; свойства скалярного произведения;
- понятие движения пространства и основные виды движения.
Уметь:
- строить точки в прямоугольной системе координат по заданным её координатам и находить координаты точки в заданной системе координат;
- выполнять действия над векторами с заданными координатами;
- доказывать, что координаты точки равны соответствующим координатам её радиус-вектора, координаты любого вектора равны разностям соответствующих координат его конца и начала;
- решать простейшие задачи в координатах;
- вычислять скалярное произведение векторов и находить угол между векторами по их координатам;
- вычислять углы между прямыми и плоскостям;
- строить симметричные фигуры.
2. Цилиндр, конус и шар.
Понятие цилиндра. Площадь поверхности цилиндра. Понятие конуса. Площадь поверхности конуса. Усечённый конус. Сфера и шар. Уравнение сферы. Взаимное расположение сферы и плоскости Касательная плоскость к сфере. Площадь сферы.
Основные цели: формирование понятия цилиндрической поверхности, цилиндра и его элементов, понятие конической поверхности, конуса и его элементов, понятия сферы, шара и их элементов; вывести формулы для вычисления площадей боковой и полной поверхности цилиндра, формулы для вычисления площадей боковой и полной поверхностей конуса и усечённого конуса, уравнение сферы в заданной прямоугольной системе координат, уравнение сферы в заданной прямоугольной системе координат, ;
Знать:
- понятие цилиндрической поверхности, цилиндра и его элементов(боковая поверхность, основания, образующие, ось, высота, радиус;
- формулы для вычисления площадей боковой и полной поверхностей цилиндра;
- понятие конической поверхности, конуса и его элементов(боковая поверхность, основание, вершина, образующая, ось, высота), усечённого конуса;
- формулы для вычисления площадей боковой и полной поверхностей конуса и усечённого конуса;
- понятия сферы, шара и их элементов(центр, радиус, диаметр);
- уравнение сферы в заданной прямоугольной системе координат;
- уравнение сферы в заданной прямоугольной системе координат;
- теоремы о касательной плоскости к сфере;
- уравнение сферы в заданной прямоугольной системе координат;
Уметь:
- решать задачи на вычисление боковой и полной поверхностей цилиндра;
- решать задачи на вычисление боковой и полной поверхностей конуса и усечённого конуса;
- решать задачи на вычисление площади сферы.
3. Объёмы тел.
Понятие объёма. Объём прямоугольного параллелепипеда. Объём прямой призмы. Объём цилиндра. Вычисление объёмов тел с помощью определенного интеграла. Объём наклонной призмы. Объём пирамиды. Объём конуса. Объём шара. Объём шарового сегмента, шарового слоя и шарового сектора. Площадь сферы.
Основные цели: формирование понятия объема тела, основные свойства объёма, правило нахождения прямой призмы; понятие призмы вписанной и призмы описанной около цилиндра, вывести формулу для вычисления объёма цилиндра, рассмотреть способы вычисления объёмов тел с помощью определённого интеграла, основную формулу для вычисления объёмов тел, вывести формулу нахождения объёма наклонной призмы, объёмов конуса и усечённого конуса, объёма шара, шарового слоя, шарового сегмента, шарового сектора; вывести формулу площади сферы.
Знать:
- понятие объёма;
- основные свойства объёма;
-правило нахождения прямой призмы; что такое призма, вписанная и призма описанная около цилиндра;
- формулу для вычисления объёма цилиндра;
- способ вычисления объёмов тел с помощью определённого интеграла, основную формулу для вычисления объёмов тел;
- формулу нахождения объёма наклонной призмы;
- формулы вычисления объёма пирамиды и усечённой пирамиды;
- формулы вычисления объёмов конуса и усечённого конуса;
- формулу объёма шара;
- определения шарового слоя, шарового сегмента, шарового сектора, формулы для вычисления их объёмов;
- формулу площади сферы.
Уметь:
- Объяснять, что такое объём тела, перечислять его свойства и применять эти свойства в несложных ситуациях;
- применять формулы нахождения объёмов призмы при решении задач;
- решать задачи на вычисления объёма цилиндра;
- воспроизводить способ вычисления объёмов тел с помощью определённого интеграла;
- применять формулу нахождения объёма наклонной призмы при решении задач;
- решать задачи на вычисление объёмов пирамиды и усечённой пирамиды;
- применять формулы вычисления объёмов конуса и усечённого конуса при решении задач;
- применять формулу объёма шара при решении задач;
- различать шаровой слой, сектор, сегмент и применять формулы для вычисления их объёмов в несложных задачах;
- применять формулу площади сферы при решении задач.
3. Обобщающее повторение. Решение задач.
Параллельность прямых и плоскостей. Перпендикулярность прямых и плоскостей. Многогранники. Метод координат в пространстве.
Цилиндр, конус и шар. Объёмы тел.
Основные цели: повторение основные определения и формул изученные в курсе геометрии ( аксиом стереометрии, понятий многогранников и их элементов, формул площадей поверхностей и объемов)
Знать:
- основные определения и формулы изученные в курсе геометрии.
Уметь:
- применять формулы при решении задач.
Календарно-тематическое планирование
| № п/п | Раздел, название урока
| Требования к уровню подготовки обучающихся | Тип и краткое содержание урока |
Дата по плану | Дата фактически |
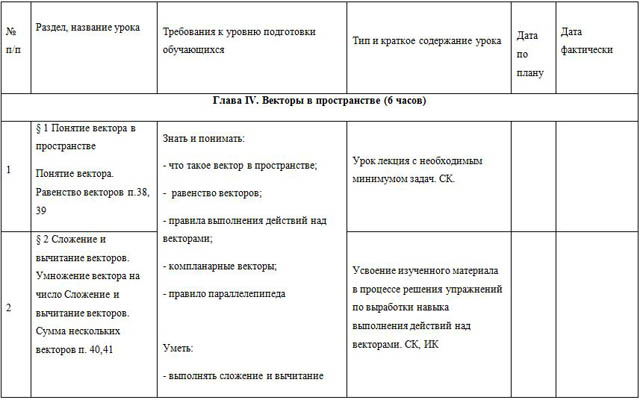
| Глава IV. Векторы в пространстве (6 часов) |
| 1 | § 1 Понятие вектора в пространстве Понятие вектора. Равенство векторов п.38, 39 | Знать и понимать: - что такое вектор в пространстве; - равенство векторов; - правила выполнения действий над векторами; - компланарные векторы; - правило параллелепипеда
Уметь: - выполнять сложение и вычитание векторов; - умножать вектор на число; - раскладывать вектор по трем некомпланарным векторам
| Урок лекция с необходимым минимумом задач. СК. |
|
|
| 2 | § 2 Сложение и вычитание векторов. Умножение вектора на число Сложение и вычитание векторов. Сумма нескольких векторов п. 40,41
| Усвоение изученного материала в процессе решения упражнений по выработки навыка выполнения действий над векторами. СК, ИК |
|
|
| 3 | Умножение вектора на число п. 42 |
|
|
| 4 | § 3 Компланарные векторы Компланарные векторы. Правило параллелепипеда. Разложение вектора по трем некомпланарным векторам п. 43-45 | Изучение и первичное закрепление новых знаний (лекция); упражнения двух типов |
|
|
| 5 | Решение задач | Уметь решать задачи с применением полученных знаний | Практикум по решению задач. ИК, ТК |
|
|
| 6 | Зачет №1 | Уметь четко отвечать на вопросы, изученные в главе IV | Урок – зачет. Индивидуальный контр. Устный по карточкам |
|
|
| Глава V. Метод координат в пространстве (11 часов) Основная цель: дать учащимся систематические сведения о методе координат в пространстве, систематизировать знания по видам движения. |
| 7 | § 1. Координаты точки и координаты вектора Прямоугольная система координат в пространстве, п. 46. | Знать и понимать: декартовы координаты в пространстве, формулы координат вектора, связь между координатами векторов и координатами точек, формулы вычисления скалярного произведения векторов, вычисления угла между прямыми, плоскостями, понятия движения в пространстве: осевая, центральная и зеркальная симметрии; параллельный перенос, поворот, свойства движения.
Уметь: выполнять действия над векторами, решать стереометрические задачи координатно-векторным методом, строить образы геометрических фигур при симметриях, параллельном переносе, повороте.
| Изучение и первичное закрепление новых знаний (лекция); упражнения двух типов.. |
|
|
| 8 | Координаты вектора, п. 47. | Усвоение изученного материала в процессе решения упражнений по выработки навыка выполнения действий над векторами. СК, ИК |
|
|
| 9 | Связь между координатами векторов и координатами точек, п. 48. | Практикум по решению упражнений. СР контролирующая (10мин). ИК, ВК. |
|
|
| 10 | Простейшие задачи в координатах, п. 49. | Исследование по проблеме: как найти координаты произвольного вектора? Закрепление материала в процессе решения задач. |
|
|
| 11 | Решение задач. | Урок обобщения и систематизации знаний. МД. Практикум по решению задач. ИК, ТК. |
|
|
| 12 | § 2. Скалярное произведение векторов. Угол между векторами. Скалярное произведение векторов, п. 46, 47. | Урок контроля, оценки и коррекции знаний учащихся. ФК. |
|
|
| 13
| Вычисление углов между прямыми и плоскостями, п. 48. | Лекция с примерами. Практикум. Обучающая СР. МД. ГК. ВК. ИК. |
|
|
| 14 | Повторение теории, решение задач по теме. | Урок лекция с необходимым минимумом задач. СК. |
|
|
| 15 | Решение задач | Урок обобщения и систематизации знаний. Практикум по решению задач. ГК устный контроль. |
|
|
| 16 | Контрольная работа №5.1 Метод координат в пространстве | Урок контроля, оценки и коррекции знаний |
|
|
| 17 | Зачет № 1 Векторы. Метод координат в пространстве | Урок – зачет. Закрепление пройденного материала. Индивидуальный контр. устный по карточкам |
|
|
| Глава VI. Цилиндр, конус и шар (13 часов) Основная цель: дать учащимся систематические сведения об основных видах тел вращения. |
| 18 | § 1. Цилиндр Понятие цилиндра. Площадь поверхности цилиндра, п. 59, 60. | Знать и понимать: понятие о телах вращения и поверхностях вращения, прямой круговой цилиндр, его элементы, осевые сечения, перпендикулярные оси; сечения, параллельные оси, прямой круговой конус, его элементы, осевые сечения конуса; сечения, перпендикулярные оси; сечения, проходящие через вершину, шар, сфера, сечение шара плоскостью, касательная плоскость к сфере, комбинация многогранников и тел вращения.
Уметь: выполнять рисунки с комбинацией круглых тел и многогранников; соотносить их с их описаниями, чертежами, аргументировать свои суждения об этом расположении, решать задачи, требующие распознавания различных тел вращения и их сечений, построения соответствующих чертеже | Урок лекция с необходимым минимумом задач. СК. |
|
|
| 19
| Решение задач по теме «Цилиндр» | Решение задач Индивидуальный контроль. |
|
|
| 20 | Решение задач по теме «Цилиндр». | Решение задач. С/Р Индивидуальный контроль. |
|
|
| 21 | § 2. Конус Понятие конуса. Площадь поверхности конуса п. 61,62. | Урок лекция с необходимым минимумом задач. |
|
|
| 22 | Усеченный конус, п. 63. | Урок лекция с необходимым минимумом задач. Практикум по решению задач. МД. |
|
|
| 23 | Решение задач по теме «Конус». | Урок повторения и обобщения некоторых подходов к решению задач на конус. СР. ИК. |
|
|
| 24 | § 3. Сфера Сфера и шар. Уравнение сферы, п. 64,65. | Лекция с набором задач. Решение задач. СР обучающая. ВК, СК. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 25 | Взаимное расположение сферы и плоскости, п. 66 | Практическая работа. Решение задач. МД. СК, ИК. |
|
|
| 26 | Касательная плоскость к сфере, п. 67 | Фронтальная работа по обсуждению подходов к решению задач по теме урока. СР обучающая. СК, ВК. |
|
|
| 27 | Площадь сферы, п. 68. | Фронтальная работа по обсуждению подходов к решению задач по теме урока. СР контр. СК, ВК. |
|
|
| 28
| Решение задач на многогранники, цилиндр, конус и шар. Изучение вопросов теории. п.69-73 | Уроки обобщения и систематизации знаний. Решение задач. С/Р Индивидуальный контроль. |
|
|
| 29
| Контрольная работа №3 «Цилиндр, конус и шар», п.59 – 73. | Урок контроля, оценки и коррекции знаний учащихся. Фронтальный тематический контроль. |
|
|
| 30 | ЗАЧЕТ№2 по теме «Цилиндр, конус и шар». | Урок – зачет. Закрепление пройденного материала. ИК устный по карточкам |
|
|
| Глава VII. Объемы тел (15 часов) Основная цель: продолжить систематическое изучение многогранников и тел вращения в ходе решения задач на вычисление их объемов. |
| 31 | §1.Объем прямоугольного параллелепипеда Понятие объема. Объем прямоугольного параллелепипеда, п. 74,75. |
Знать и понимать: понятие об объеме, основные свойства объемов, формулы для вычисления объемов многогранников: прямоугольного параллелепипеда, призмы, пирамиды, формулы для вычисления объемов тел вращения: цилиндра, конуса, шара. Уметь: уметь решать задачи вычислительного характера на непосредственное применение формул объемов многогранников и круглых тел, в том числе в ходе решения несложных практических задач. | Комбинированный урок: лекция, практическая работа, работа с учебником |
|
|
| 32 | Объем прямой призмы, основанием которой является прямоугольный треугольник, п. 75. | Практический урок + объяснение. Проверочная работа. |
|
|
| 33
| § 2. Объем прямой призмы и цилиндра. Теоремы об объеме прямой призмы и цилиндра, п. 76,77. | Комбинированный урок: лекция, практическая работа, работа с учебником. |
|
|
| 34 | Повторение вопросов теории и решение задач. | Усвоение изученного материала в процессе решения задач. МД. |
|
|
| 35 | Повторение вопросов теории и решение задач. |
|
|
|
| 36
| § 3. Объем наклонной призмы, пирамиды и конуса. Вычисление объемов тел с помощью определенного интеграла. Объем наклонной призмы, п. 78,79. | Комбинированные уроки: лекция, практикум, проверочная СР обучающая.. |
|
|
| 37 | Объем пирамиды, п. 80. | Комбинированные уроки: лекция, исследование, СР контролирующая. |
|
|
| 38 | Объем конуса, п. 81. | Лекция. Усвоение изученного материала в процессе решения задач. |
|
|
| 39 | Решение задач | Урок контроля, оценки и коррекции знаний. Фронтальный письменный контроль. |
|
|
| 40 | § 4. Объем шара и площадь сферы Объем шара, п. 82. | Комбинированные уроки: лекция, практикум, обучающая С/Р. |
|
|
| 41 | Объем шарового сегмента, шарового слоя и шарового сектора, п.83. | Лекция. Исследовательская деятельность. |
|
|
| 42 | Площадь сферы, п. 84. | Комбинированный урок: лекция, практическая работа, работа с учебн. |
|
|
| 43 | Решение задач. | Усвоение изученного материала в процессе решения задач. СР. |
|
|
| 44 | Контрольная работа №7.1 «Объемы тел», п.74-84 | Урок контроля, оценки и коррекции знаний. Фронтальный письменный контроль |
|
|
| 45 | ЗАЧЕТ№3 по теме «Объемы тел». | Урок – зачет. Урок контроля, оценки и коррекции знаний. ФК устный контроль. |
|
|
| Заключительное повторение при подготовке к итоговой аттестации по геометрии |
| 46 | Куб | Уметь: решать геометрические задачи на экстремумы, решаемые введением вспомогательного угла, применять изученный теоретический материал при решении различных планиметрических и стереометрических задач, решать задачи на комбинации тел. | Уроки обобщения и систематизации знаний. Практикумы по решению задач. СР контролирующего характера с использованием материалов ЕГЭ
|
|
|
| 47 | Параллелепипед |
|
|
| 48 | Призма |
|
|
| 49
| Пирамида |
|
|
| 50 | Многогранники |
|
|
| 51 | Цилиндр, конус, шар |
|
|
| 52 | Вписанные и описанные фигуры в пространстве |
|
|
| 53
| Диагностическая работа |
|
|
| 54 | Угол между прямыми |
|
|
| 55
| Угол между прямыми |
|
|
| 56
| Угол между прямой и плоскостью |
|
|
| 57
| Угол между прямой и плоскостью |
|
|
| 58 | Угол между двумя плоскостями |
|
|
| 59 | Угол между двумя плоскостями |
|
|
| 60 | Расстояние от точки до прямой |
|
|
| 61 | Расстояние от точки до прямой |
|
|
| 62 | Расстояние от точки до плоскости |
|
|
| 63 | Расстояние от точки до плоскости |
|
|
| 64 65 | Расстояние между двумя прямыми |
|
|
| 66 | Диагностическая работа С2 |
|
|
| 67 68 | Анализ результатов диагностической работы Решение задач |
|
|
| 69 70 | Решение задач |
|
|
Ресурсное обеспечение реализации рабочей программы
1. Программы по геометрии к учебнику 10-11. Автор Атанасян Л.С., В. Ф. Бутузов, С. Б. Кадомцев и др. (Составитель сборника программ: Т. А .Бурмистрова. «Просвещение», 2009)
2. Геометрия, учеб. для 10-11 кл./ [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.] – 16-е изд. – М.: Просвещение, 2008
3. Геометрия: рабочая тетрадь для 11 кл. /Л. С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков, И.И. Юдина. – М.: Просвещение, 2010
4. Зив Б.Г. Геометрия: Дидактические материалы для 11 класса/ Б.Г. Зив, В.М. Мейлер. – М.: Просвещение, 2007
5. Изучение геометрии в 10-11 классах: методические рекомендации: кн. для учителя/ С.М. Саакян, В.Ф. Бутузов]- М.: Просвещение, 2007
6. Смирнов В.А. Планиметрия: пособие для подготовки к ЕГЭ/ Под ред. И.В. Ященко и А.В. Семёнова. – М.: МЦНМО, 2015
7. Смирнов В.А. Стереометрия: пособие для подготовки к ЕГЭ/ Под ред. И.В. Ященко и А.В. Семёнова. – М.: МЦНМО, 2009

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по учебному предмету "Математика" (геометрия, 11 класс) (47.01 КB)
Рабочая программа по учебному предмету "Математика" (геометрия, 11 класс) (47.01 КB)
 0
0 455
455 50
50 Нравится
0
Нравится
0









