Специально для учителей!

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Разработки / Математика / Планирование / Рабочая программа по математике для СПО (специальность автомеханик)

Рабочая программа по математике для СПО (специальность автомеханик)

Рабочая программа учебной дисциплины является частью примерной основной профессиональной образовательной программы в соответствии с федеральным государственным образовательным стандартом по программе подготовки квалифицированных рабочих и служащих по профессии 190631.01 «Автомеханик».

Таймуллина Татьяна Николаевна, ГАОУ СПО "Нурлатский аграрный техникум"

28.11.2014

Описание разработки

Область применения программы.

Рабочая программа учебной дисциплины является частью примерной основной профессиональной образовательной программы в соответствии с федеральным государственным образовательным стандартом по программе подготовки квалифицированных рабочих и служащих по профессии 190631. 01 Автомеханик.

Место учебной дисциплины в структуре основной профессиональной образовательной программы:

дисциплина входит в общеобразовательный цикл.

Цель и задачи учебной дисциплины – требования к результатам освоения учебной дисциплины:

Примерная программа ориентирована на достижение следующих целей:

формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;

развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;

овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения смежных естественно-научных дисциплин на базовом уровне и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;

воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.

В результате освоения учебной дисциплины обучающийся должен уметь:

Алгебра.

выполнять арифметические действия над числами, сочетая устные и письменные приемы; находить приближенные значения величин и погрешности вычислений (абсолютная и относительная); сравнивать числовые выражения;

находить значения корня, степени, логарифма, тригонометрических выражений на основе определения, используя при необходимости инструментальные средства; пользоваться приближенной оценкой при практических расчетах;

выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

для практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.

Рабочая программа по математике для СПО (специальность автомеханик)

Функции и графики.

вычислять значение функции по заданному значению аргумента при различных способах задания функции;

определять основные свойства числовых функций, иллюстрировать их на графиках;

строить графики изученных функций, иллюстрировать по графику свойства элементарных функций;

использовать понятие функции для описания и анализа зависимостей величин;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.

Начала математического анализа.

находить производные элементарных функций;

использовать производную для изучения свойств функций и построения графиков;

применять производную для проведения приближенных вычислений, решать задачи прикладного характера на нахождение наибольшего и наименьшего значения;

вычислять в простейших случаях площади и объемы с использованием определенного интеграла;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.

Уравнения и неравенства.

решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы;

использовать графический метод решения уравнений и неравенств;

изображать на координатной плоскости решения уравнений, неравенств и систем с двумя неизвестными;

составлять и решать уравнения и неравенства, связывающие неизвестные величины в текстовых (в том числе прикладных) задачах.

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

для построения и исследования простейших математических моделей.

Весь материал - в документе.

Содержимое разработки

Министерство образования и науки Республики Татарстан

Государственное автономное образовательное учреждение

среднего профессионального образования

«Нурлатский аграрный техникум»

СОГЛАСОВАНО	УТВЕРЖДАЮ
Заместитель директора по НМР	Заместитель директора по УР
_______________ И.Р.Зайцева	_______________ С.В.Исаева
«___»_____________2014г.	«___»______________2014г.

рабочая ПРОГРАММА

учебной дисциплины

«математика».

Рассмотрена на заседании предметно-цикловой комиссии

общеобразовательных дисциплин

Протокол № ___

от «___»___________ 2014г.

Председатель ПЦК_______________

2014 г.

Организация-разработчик: Государственное автономное образовательное учреждение среднего профессионального образования «Нурлатский аграрный техникум».

Разработчик: преподаватель Таймуллина Татьяна Николаевна.

СОДЕРЖАНИЕ

	стр.
1.ПАСПОРТ РАБОЧЕЙ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ	1-7
2. СТРУКТУРА и содержание УЧЕБНОЙ ДИСЦИПЛИНЫ	8-23
3. условия реализации УЧЕБНОЙ ДИСЦИПЛИНЫ	24-26
4 Контроль и оценка результатов освоения УЧЕБНОЙ ДИСЦИПЛИНЫ	27-28

ПАСПОРТ РАБОЧЕЙ ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ

Математика

Область применения программы

Место учебной дисциплины в структуре основной профессиональной образовательной программы:

дисциплина входит в общеобразовательный цикл.

Цель и задачи учебной дисциплины – требования к результатам освоения учебной дисциплины:

Примерная программа ориентирована на достижение следующих целей:

формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения смежных естественно-научных дисциплин на базовом уровне и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;

воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей

В результате освоения учебной дисциплины обучающийся должен уметь:

Алгебра

выполнять арифметические действия над числами, сочетая устные и письменные приемы; находить приближенные значения величин и погрешности вычислений (абсолютная и относительная); сравнивать числовые выражения;
находить значения корня, степени, логарифма, тригонометрических выражений на основе определения, используя при необходимости инструментальные средства; пользоваться приближенной оценкой при практических расчетах;
выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

для практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.

Функции и графики

вычислять значение функции по заданному значению аргумента при различных способах задания функции;
определять основные свойства числовых функций, иллюстрировать их на графиках;
строить графики изученных функций, иллюстрировать по графику свойства элементарных функций;
использовать понятие функции для описания и анализа зависимостей величин;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.

Начала математического анализа

находить производные элементарных функций;
использовать производную для изучения свойств функций и построения графиков;
применять производную для проведения приближенных вычислений, решать задачи прикладного характера на нахождение наибольшего и наименьшего значения;
вычислять в простейших случаях площади и объемы с использованием определенного интеграла;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.

Уравнения и неравенства

решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы;
использовать графический метод решения уравнений и неравенств;
изображать на координатной плоскости решения уравнений, неравенств и систем с двумя неизвестными;
составлять и решать уравнения и неравенства, связывающие неизвестные величины в текстовых (в том числе прикладных) задачах.

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

для построения и исследования простейших математических моделей.

КОМБИНАТОРИКА, СТАТИСТИКА И ТЕОРИЯ ВЕРОЯТНОСТЕЙ

уметь:

решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

для анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера.

ГЕОМЕТРИЯ

распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.

В результате освоения учебной дисциплины обучающийся должен знать:

значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира.

Рекомендуемое количество часов на освоение рабочей программы учебной дисциплины (по ФГОС):

максимальной учебной нагрузки обучающегося 443 часа, в том числе:

обязательной аудиторной учебной нагрузки обучающегося 295 часов;

самостоятельной работы обучающегося 148 часов;

практической работы обучающегося 40 часов.

СТРУКТУРА И СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

2.1. Объем учебной дисциплины и виды учебной работы

Вид учебной работы	Объем часов
Максимальная учебная нагрузка (всего)	443
Обязательная аудиторная учебная нагрузка (всего)	295
в том числе:
практические занятия	40
Самостоятельная работа обучающегося (всего)	148
Итоговая аттестация После 1курса (2 семестра) – дифференцированный зачет После 2 курса (4 семестра) - экзамен

2.2. Рабочий тематический план и содержание учебной дисциплины «Математика»

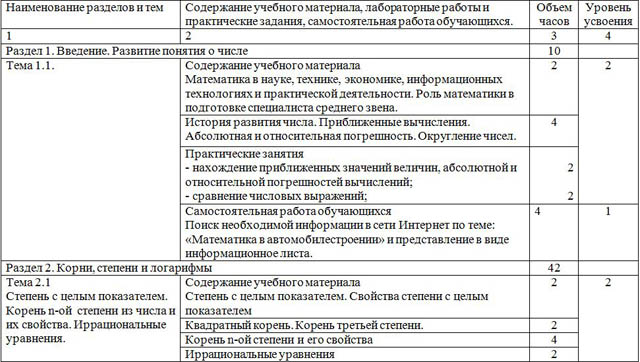
Наименование разделов и тем	Содержание учебного материала, лабораторные работы и практические задания, самостоятельная работа обучающихся.	Объем часов	Уровень усвоения
1	2	3	4
Раздел 1. Введение. Развитие понятия о числе		10
Тема 1.1.	Содержание учебного материала Математика в науке, технике, экономике, информационных технологиях и практической деятельности. Роль математики в подготовке специалиста среднего звена.	2	2
	История развития числа. Приближенные вычисления. Абсолютная и относительная погрешность. Округление чисел.	4
	Практические занятия - нахождение приближенных значений величин, абсолютной и относительной погрешностей вычислений; - сравнение числовых выражений;	2 2
	Самостоятельная работа обучающихся Поиск необходимой информации в сети Интернет по теме: «Математика в автомобилестроении» и представление в виде информационное листа.	4	1
Раздел 2. Корни, степени и логарифмы		42
Тема 2.1 Степень с целым показателем. Корень n-ой степени из числа и их свойства. Иррациональные уравнения.	Содержание учебного материала Степень с целым показателем. Свойства степени с целым показателем	2	2
	Квадратный корень. Корень третьей степени.	2
	Корень n-ой степени и его свойства	4
	Иррациональные уравнения	2
	Практические занятия Тождественные преобразования степенных и иррациональных выражений. Решение иррациональных уравнений и систем.	2
	Самостоятельная работа обучающихся Решение тестовых заданий по теме «Иррациональные уравнения»	2
Тема 2.2. Степень с рациональным показателем, с действительными показателями. Решение показательных уравнений	Содержание учебного материала Степень с рациональным показателем и их свойства	4	2
	Степени с действительными показателями (Показательная функция)	2
	Решение показательных уравнений и неравенств	2
	Самостоятельная работа обучающихся Решение показательных уравнений и неравенств	2
Тема 2.3. Логарифмы и их свойства. Преобразование рациональных и иррациональных выражений	Содержание учебного материала Логарифмы и их свойства	4	2
	Логарифмы и их свойства. Десятичные и натуральные логарифмы	4
	Преобразование рациональных выражений	2
	Преобразование иррациональных выражений	2
	Практические занятия 1. Логарифм, правила вычисления логарифмов. 2. Свойства логарифмов	2
	Самостоятельная работа обучающихся Подготовка сообщения по теме «История возникновения логарифмов»	4
Тема 2.4. Преобразование степенных, показательных и логарифмических выражений.	Содержание учебного материала Преобразование степенных выражений	2	2
	Преобразование показательных выражений	2
	Преобразование логарифмических выражений	2
	Преобразование алгебраических выражений	1
	Контрольная работа № 1	1
	Самостоятельная работа обучающихся Составление кроссворда по теме «Корни, степени и логарифмы»	4
Раздел 3. Прямые и плоскости в пространстве		26
Тема 3. 1. Параллельность прямых и плоскостей	Содержание учебного материала Параллельность прямых, прямой и плоскости (Параллельность прямой и плоскости)	2	2
	Взаимное расположение прямых в пространстве (двух прямых в пространстве)	2
	Параллельность плоскостей	4
	Самостоятельная работа обучающихся Подготовить вопросы по теме «Параллельность плоскостей», для взаимоконтроля.	2
Тема 3.2. Решение задач по теме «Параллельность прямых и плоскостей»	Содержание учебного материала Решение задач по теме «Параллельность прямых и плоскостей»	4	2
	Практические занятия Решение задач по теме «Параллельность прямых и плоскостей»	2
	Самостоятельная работа обучающихся Подготовка реферата «Параллельное проектирование и его свойства».	4
Тема 3.3. Перпендикулярность прямых и плоскостей.	Содержание учебного материала Перпендикулярность прямой и плоскости. Перпендикуляр и наклонная. Угол между прямой и плоскостью	2	2
	Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей	3
	Самостоятельная работа обучающихся Подготовить вопросы по теме «Перпендикулярность двух плоскостей», для взаимоконтроля.	2
Тема 3.4. Решение задач по теме «Перпендикулярность прямых и плоскостей»	Содержание учебного материала Решение задач по теме «Перпендикулярность прямых и плоскостей»	4	2
	Практические занятия Решение задач по теме «Перпендикулярность прямых и плоскостей»	2
	Контрольная работа № 2	1
	Самостоятельная работа обучающихся Подготовить типовые задачи по теме «Параллельность прямых и плоскостей» для взаимоконтроля.	4
Раздел 4. Элементы комбинаторики		16
Тема 4.1. Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов.	Содержание учебного материала Основные понятия комбинаторики	2	1
	Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов	4
	Решение задач на подсчет числа размещений, перестановок, сочетаний и на перебор вариантов	4
	Практические занятия - Задачи на подсчет числа размещений, перестановок, сочетаний; - Решение задач на перебор вариантов; - Решение задач на подсчет числа размещений, перестановок, сочетаний и на перебор вариантов.	2
	Самостоятельная работа обучающихся Составить кроссворд по теме «Элементы комбинаторики»	2
Тема 4.2. Формула бинома Ньютона. . Свойства биноминальных коэффициентов. Треугольник Паскаля	Содержание учебного материала Формула бинома Нъютона	2	1
	Свойства биномиальных коэффициентов.	1	1
	Контрольная работа № 3	1
	Самостоятельная работа обучающихся Внеаудиторное самостоятельное изучений темы: «Треугольник Паскаля»	2
Раздел 5. Многогранники		40
Тема 5.1. Вершины, ребра, грани многогранника. (Теорема Эйлера). Призма. Прямая и наклонная призма.	Содержание учебного материала Вершины, ребра, грани многогранника. (Теорема Эйлера)	2	3
	Призма. Прямая и наклонная призма	2
	Решение задач по теме «Призма. Прямая и наклонная призма»	4
	Самостоятельная работа обучающихся Построение прямой и наклонной призмы. Подготовить информационные листы по теме «Призма. Прямая и наклонная призма»	4
Тема 5.2. Правильная призма. Параллелепипед. Куб.	Содержание учебного материала Правильная призма. Параллелепипед. Куб.	2	3
	Решение задач по теме «Правильная призма. Параллелепипед. Куб.»	6
	Самостоятельная работа обучающихся Решение задач на вычисление площади поверхности призмы.	4
Тема 5.3. Пирамида. Правильная пирамида (Усеченная пирамида). Симметрия в кубе, в параллелепипеде.	Содержание учебного материала Пирамида. Правильная пирамида (Усеченная пирамида. Тетраэдр).	6	2
	Симметрия в кубе, в параллелепипеде.	2
	Практические занятия Решение задач по теме: «Пирамида. Правильная пирамида»	4
	Самостоятельная работа обучающихся Внеаудиторное самостоятельное изучение темы «Усеченная пирамида»; Подготовить презентацию «Многогранники».	6
Тема 5.4. Сечения куба, призмы и пирамиды. Представление о правильных многогранниках	Содержание учебного материала Сечения куба, призмы и пирамиды	4	2
	Представление о правильных многогранниках	3
	Практические занятия Решение задач на построение сечений куба, призмы и пирамиды	4
	Контрольная работа № 4	1
	Самостоятельная работа обучающихся 1. Изготовление моделей многогранников. 2 Составление презентаций по теме: « Сечения призмы и пирамиды»	8
Раздел 6. Основы тригонометрии		26
Тема 6.1. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества, формулы приведения.	Содержание учебного материала Радианная мера угла. Вращательное движение.	2	2
	Синус, косинус, тангенс и котангенс числа	2
	Основные тригонометрические тождества. Формулы приведения	6
	Практические занятия Преобразования тригонометрических выражений	2
	Самостоятельная работа обучающихся Составление тестовых заданий по теме: « Преобразования тригонометрических выражений»	7
Тема 6.2. Синус, косинус, тангенс и котангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла	Содержание учебного материала Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла.	5	2
	Преобразование суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента	6
	Практические занятия Преобразования тригонометрических выражений	2
	Контрольная работа № 5	1
	Самостоятельная работа обучающихся 1. Подготовка сообщения на тему «История тригонометрии и ее роль в изучении естественно-математических наук» 2. Решение задач и упражнений по образцу по теме: «Формулы тригонометрии»	7
Раздел 7. Функции, их свойства и графики. Степенные, показательные, логарифмические и тригонометрические функции		24
Тема 7.1. Функции и их графики. Преобразование графиков.	Содержание учебного материала Функции. Область определения и множество значений.	2	2
	График функции, построение графиков функций, заданных различными способами.	2
	Преобразования графиков. Параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой x=y, растяжение и сжатие вдоль осей координат.	4
	Практические занятия Преобразования графиков. Параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой x=y, растяжение и сжатие вдоль осей координат	2	2
	Самостоятельная работа обучающихся Подготовка сообщения на тему «История тригонометрии и ее роль в изучении естественно-математических наук»	2
Тема 7.2. Свойства функции	Содержание учебного материала Свойства функции: монотонность, четность, нечетность, ограниченность, периодичность	2	2
	Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума. Графическая интерпретация.	4
	Примеры функциональных зависимостей в реальных процессах и явлениях.	2
	Самостоятельная работа обучающихся Подготовить презентацию на любую из тем: «Функции и их графики», «Преобразование графиков», «Свойства функций», «Степенные функции», «Показательные функции», «Логарифмическая функция», «Тригонометрическая функция».	12
Тема 7.3. Обратные функции. Область определения и область значений обратной функции. График обратной функции. Обратные тригонометрические функции.	Содержание учебного материала Обратные функции. Область определения и область значений обратной функции. График обратной функции.	2	1
	Арксинус, арккосинус и арктангенс	3
	Контрольная работа № 6	1
	Самостоятельная работа обучающихся Решение задач и упражнений по образцу по теме: « Формулы тригонометрии»	5
Раздел 8. Координаты и векторы		20
Тема 8.1. Понятие вектора. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число. Компланарные векторы. Разложение вектора по трем некомпланарным векторам. Прямоугольная система координат в пространстве. Координаты вектора	Содержание учебного материала Понятие вектора. Модуль вектора. Равенство векторов	1	2
	Сложение векторов. Умножение вектора на число	2
	Компланарные векторы. Разложение вектора по трем некомпланарным векторам.	3
	Прямоугольная система координат в пространстве. Координаты вектора	2
	Самостоятельная работа обучающихся Решение задач и упражнений по образцу по теме: « Векторы» Выполнение тестов по теме: « Правила сложения векторов. Скалярное произведение векторов»	5
Тема 8.2. Связь между координатами векторов и координатами точек. Формула расстояния между двумя точками. Угол между двумя векторами. Скалярное произведение векторов. Использование координат и векторов при решении математических и прикладных задач	Содержание учебного материала Связь между координатами векторов и координатами точек. Формула расстояния между двумя точками	3	2
	Угол между двумя векторами. Скалярное произведение векторов	2
	Центральная симметрия. Осевая симметрия. Зеркальная симметрия. Параллельный перенос.	2
	Использование координат и векторов при решении математических и прикладных задач	2
	Практические занятия Решение математических и прикладных задач с использованием координат и векторов	2
	Контрольная работа № 7	1
	Самостоятельная работа обучающихся 1. Составление математического диктанта по теме: « Координаты вектора» 2. Решение задач по теме: « Векторы в пространстве» 3. Домашняя контрольная работа по теме: « Координаты вектора»	6
Раздел 9. Тела и поверхности вращения		14
Тема 9.1. Цилиндр. Основание, высота, боковая поверхность, образующая, развертка	Содержание учебного материала Цилиндр. Основание, высота, боковая поверхность, образующая, развертка	4	2
	Самостоятельная работа обучающихся Составление кроссворда по теме: « Тела вращения»	2
Тема 9.2. Конус. Основание, высота, боковая поверхность, образующая, развертка.	Содержание учебного материала Конус. Основание, высота, боковая поверхность, образующая, развертка. Усеченный конус	4
	Практические занятия Решение задач на вычисление площадей поверхностей тел вращения.	2
	Контрольные работы
	Самостоятельная работа обучающихся Решение задач и упражнений по образцу по теме: « Площади поверхностей тел вращения»	2
Тема 9.3. Сфера и шар, их сечения	Содержание учебного материала Сфера и шар, их сечения.	3	2
	Контрольная работа № 8	1
	Самостоятельная работа обучающихся Изготовление моделей тел вращения.	2
Раздел 10. Начала математического анализа		26
Тема 10.1. Последовательности. Способы задания и свойства числовых последовательностей. Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Суммирование последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма. Понятие о непрерывности функции.	Содержание учебного материала Последовательности. Способы задания и свойства числовых последовательностей	2	2
	Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности.	2
	Суммирование последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма. Понятие о непрерывности функции.	2
	Самостоятельная работа обучающихся Внеаудиторное изучение темы «Понятие о непрерывности функции»	3
Тема 10.2. Производная. Понятие о производной функции, её геометрический и физический смысл. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Производные обратной функции и композиции функции.	Содержание учебного материала Производная. Понятие о производной функции, её геометрический и физический смысл. Уравнение касательной к графику функции.	2	2
	Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков	4
	Практические занятия Решение задач по теме: «Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков»	2
	Самостоятельная работа обучающихся Внеаудиторное изучение темы «Производные обратной функции и композиции функции».	3
Тема 10.3. Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Вторая производная, ее геометрический и физический смысл. Применение производной к исследованию функций и построению графиков. Нахождение скорости для процесса, заданного формулой и графиком.	Содержание учебного материала Примеры использования производной для нахождения наилучшего решения в прикладных задачах	2	2
	Вторая производная, ее геометрический и физический смысл. Применение производной к исследованию функций и построению графиков.	2
	Нахождение скорости для процесса, заданного формулой и графиком.	2
	Самостоятельная работа обучающихся Составить информационный лист по теме «Применение производной к исследованию функций».	3
Тема 10.4. Первообразная и интеграл. Применение определенного интеграла для нахождения площади криволинейной трапеции. Формула Ньютона—Лейбница. Примеры применения интеграла в физике и геометрии	Содержание учебного материала Первообразная. Правила нахождения первообразных.	1	1
	Применение определенного интеграла для нахождения площади криволинейной трапеции. Формула Ньютона—Лейбница.	2
	Вычисление площадей фигур с помощью интегралов. Применение интегралов для решения физических задач	2
	Контрольная работа № 9	1
	Самостоятельная работа обучающихся Решение прикладных задач с помощью определённого интеграла	3
Раздел 11. Измерения в геометрии		18
Тема 11.1. Объем и его измерение. Интегральная формула объема. Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра	Содержание учебного материала Объем и его измерение. Интегральная формула объема.	2	2
	Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра	2
	Практические занятия Решение задач на вычисление объема куба, прямоугольного параллелепипеда, призмы, цилиндра	2
	Контрольные работы
	Самостоятельная работа обучающихся Решение задач на вычисление объёмов многогранников.	2
Тема 11.2. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса.	Содержание учебного материала Формулы объема пирамиды и конуса.	2	2
	Формулы площади поверхностей цилиндра и конуса	2
	Самостоятельная работа обучающихся Решение задач и упражнений по образцу по теме: « Объём цилиндра и конуса»	2
Тема 11.3. Формулы объема шара и площади сферы.	Содержание учебного материала Формулы объема шара и площади сферы	4	2
Тема 11.3. Формулы объема шара и площади сферы.	Самостоятельная работа обучающихся Подготовить презентацию «Формулы объема шара и площади сферы»	2	2
Тема 11.4. Подобие тел. Отношение площадей поверхностей и объемов подобных тел.	Содержание учебного материала Подобие тел. Отношение площадей поверхностей и объемов подобных тел.	3	2
	Контрольная работа № 10	1
	Самостоятельная работа обучающихся Подготовить типовые задачи по теме «Измерения в геометрии», для взаимоконтроля	2
Раздел 12. Элементы теории вероятностей. Элементы математической статистики		10	2
Тема 12.1. Событие, вероятность события, сложение и умножение вероятностей. Понятие о независимости событий. Дискретная случайная величина, закон ее распространения	Содержание учебного материала Событие, вероятность события, сложение и умножение вероятностей	2
	Понятие о независимости событий. Дискретная случайная величина, закон ее распространения. Числовые характеристики дискретной случайной величины. Понятие о законе больших чисел	2
	Практические занятия Решение задач по теме: «Элементы теории вероятностей»	2
	Самостоятельная работа обучающихся Подготовка сообщения по теме: « История происхождения теории вероятностей»	3
Тема 12.2. Представление данных (таблицы, диаграммы, графики).	Содержание учебного материала Представление данных (таблицы, диаграммы, графики). Генеральная совокупность, выборка, среднее арифметическое, медиана.	2	1
	Решение практических задач с применением вероятностных методов.	2
	Самостоятельная работа обучающихся Создание презентации по теме: «Элементы математической статистики»	3
Раздел 13. Уравнения и неравенства		23
Тема 13.1. Равносильность уравнений, неравенств, систем. Рациональные, иррациональные, показательные и тригонометрические уравнений и системы. Основные приемы их решения (разложение на множители, введение новых неизвестных, подстановка, графический метод)	Содержание учебного материала Равносильность уравнений, неравенств, систем	1	2
	Рациональные, иррациональные, показательные и тригонометрические уравнений и системы.	2
	Основные приемы их решения (разложение на множители, введение новых неизвестных, подстановка, метод интервалов, графический метод)	4
	Практические занятия Рациональные, иррациональные, показательные уравнения, системы. Основные методы решения.	2
	Самостоятельная работа обучающихся Внеаудиторное узучение темы: Метод интервалов Решение содержательных задач из различных областей науки и практики методом составления уравнений.	4
Тема 13.2. Рациональные, иррациональные, показательные и тригонометрические неравенства. Основные приемы их решения.	Содержание учебного материала Рациональные, иррациональные, показательные и тригонометрические неравенства.	2	2
	Основные приемы их решения рациональных, иррациональных, показательных и тригонометрических неравенств.	2
	Самостоятельная работа обучающихся Составление содержательных задач, решаемые составлением неравенства.	6
Тема 13.3. Использование свойств и графиков функций при решении уравнений и неравенств.	Содержание учебного материала Использование свойств и графиков функций при решении уравнений и неравенств.	2	2
	Самостоятельная работа обучающихся Выполнение тестовых заданий по теме «Неравенства»	4	2
Тема 13.4. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем . Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений	Содержание учебного материала Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем	2	2
	Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений	5	2
	Контрольная работа № 12	1	2
	Самостоятельная работа обучающихся Решение содержательных задач из различных областей науки и практики.	4	2
Всего:		295

Для характеристики уровня освоения учебного материала используются следующие обозначения:

1. – ознакомительный (узнавание ранее изученных объектов, свойств);

2. – репродуктивный (выполнение деятельности по образцу, инструкции или под руководством)

3. – продуктивный (планирование и самостоятельное выполнение деятельности, решение проблемных задач)

3. УСЛОВИЯ РЕАЛИЗАЦИИ ПРОГРАММЫ ДИСЦИПЛИНЫ

УСЛОВИЯ РЕАЛИЗАЦИИ УЧЕБНОЙ ДИСЦИПЛИНЫ

3.1. Требования к минимальному материально-техническому обеспечению

Реализация учебной дисциплины требует наличия учебного кабинета

« Математика»:

3.1.1. Учебно – практическое оборудование кабинета:

аудиторная доска с магнитной поверхностью;
комплект измерительных инструментов: линейка, транспортир, угольник, циркуль;
комплект стереометрических тел (демонстрационный);
комплект стереометрических тел (раздаточный);
набор планиметрических фигур;

3.1.2. Специализированная учебная мебель:

письменные столы по числу рабочих мест обучающихся;
шкаф секционный для хранения литературы и демонстрационного оборудования;
стенды, содержащие справочный материал;
ящики для хранения таблиц;

3.1.3. Печатные пособия:

таблицы по геометрии;
таблицы по алгебре и началам анализа для 10-11 классов;
портреты выдающихся деятелей математики;

3.1.4. Учебно – методический комплекс:

учебно – практическое издание (практикум);
комплект контрольно – измерительных материалов по дисциплине;
сборники экзаменационных работ для проведения государственной (итоговой) аттестации по математике;

3.1.5. Технические средства обучения:

интерактивная доска с лицензионным программным обеспечением и мультимедиапроектор

3.2. Информационное обеспечение

Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы:

Основные источники:

Башмаков М.И. «Математика» учебник для учреждений начального и среднего проф. образования. – Издательский центр «Академия», 2011.
Башмаков М.И. Математика. Задачник: учеб. пособие для образоват. учреждений нач. и сред. проф. образования.- М.: Издательский центр «Академия», 2012.
Башмаков М.И. Математика. Книга для преподавателей: методическое пособие для НПО, СПО. - М.: Издательский цент «Академия», 2013 г.
Башмаков М.И. Математика. Сборник задач профильной направленности: учеб. пособие для учреждений нач. и сред. проф. образования. – М.: Издательский центр «Академия», 2012 .
Гусев В.А. Математика для профессий и специальностей социально – экономического профиля: учебник для образоват. учреждений нач. и сред. Проф. Образования. – 4-е изд., стер. – М.: Издательский центр «Академия», 2012.
Дорофеев Г.В. , Муравин Г.К., Седова Е.А., Сборник заданий для

Подготовки и проведения письменного экзамена по математике

(курс А) и алгебре и началам агнализа (курс В) за курс средней школы. 11 класс: Эксперимент. пособие.-3-е изд., исп.-М.: Дрофа, 2010.

Дополнительные источники:

Рурукин А.Н. , Бровкова Е.В., Поурочные разработки по алгебре и

началам анализа: 10 класс. – М.: ВАКО, 2009.- 352 с.

Рурукин А.Н. , Поурочные разработки по алгебре и началам анализа: 11 класс. – М.: ВАКО, 2009.- 336 с..
Студенецкая В.Н.. Решение задач по статистике, комбинаторике и

теории вероятностей, 7 – 9 классы - Изд. 2-е, испр. – Волгоград:

Учитель, 2008.

Колмогоров А.Н., Абрамов А. М., Дудницын Ю. П.. Алгебра и начала

анализа 10-11 класс.- 13 –е издание.- М. : Просвещение, 2004.- 384 с.

5. Мордкович А.Г. Алгебра и начала анализа. 10-11 кл.: В двух частях. Ч.

1: Учеб. для общеобразоват. Учреждений. – 6-е изд. – М.: Мнемозина,

2005. – 375 с.: ил.

6. Мордкович А.Г. Алгебра и начала анализа. 10-11 кл.: В двух частях. Ч.

2: Задачник для общеобразоват. Учреждений. – 6-е изд. – М.:

Мнемозина, 2005. – 375 с.: ил.

7. Мордкович А.Г., Семёнов П.В. События. Вероятности. Статистическая

обработка данных. Доп. параграфы к курсу алгебры 7 – 9 кл.

общеобраз. Учреждений. – 2-е изд. – М.: Мнемозина, 2004.- 112 с.

Журналы и газеты:

Еженедельная учебно-методическая газета «Математика».
Журнал « Математика в школе»

КОНТРОЛЬ И ОЦЕНКА РЕЗУЛЬТАТОВ ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ

Контроль и оценка результатов освоения учебной дисциплины осуществляется преподавателем в процессе проведения практических занятий, тестирования, а также выполнения обучающимися индивидуальных заданий, проектов, исследований.

Оценка качества освоения учебной программы включает текущий контроль успеваемости, промежуточную аттестацию по итогам освоения дисциплины.

Результаты обучения (освоенные умения, усвоенные знания)	Формы и методы контроля и оценки результатов обучения
Умения:
решать линейные и квадратные уравнения и уравнения, сводящиеся к ним;	Входной контроль: тестирование Текущий контроль: практические работы, тесты, самостоятельные работы, графические работы, кроссворды Тематический контроль: контрольная работа, домашняя контрольная работа Итоговый контроль: экзамен
выполнять действия с действительными числами, пользоваться калькулятором для вычислений, находить приближённые вычисления;
решать линейные и квадратные неравенства, системы неравенств;
производить действия с векторами;
использовать свойства элементарных функций при решении задач и упражнений;
выполнять тождественные преобразования со степенными, логарифмическими и тригонометрическими выражениями;
использовать свойства элементарных функций при решении задач и упражнений;
вычислять производные и первообразные, определённые интегралы, применять определённый интеграл для нахождения площади криволинейной трапеции;
применять свойства прямых и плоскостей в пространстве при решении задач;
изображать геометрические тела на плоскости, строить их сечения плоскостью;
решать задачи на вычисление площадей поверхностей и объёмов геометрических тел;
применять основные положения теории вероятностей и математической статистики в профессиональной деятельности;
Знания:
основные функции, их графики и свойства;	Входной контроль: тестирование Текущий контроль: самостоятельные работы , тесты, практические работы, графические работы, математические диктанты, устные опросы Тематический контроль: контрольная работа, домашняя контрольная работа Итоговый контроль: экзамен
основы дифференциального и интегрального исчислений;
алгоритмы решения тригонометрических, показательных, логарифмических уравнений и неравенств;
основные свойства элементарных функций;
основные понятия векторной алгебры;
основы линейной алгебры;
основные понятия и определения стереометрии;
свойства геометрических тел и поверхностей;
формулы площадей поверхностей и объёмов;
основные понятия комбинаторики; статистики, теории вероятностей;