Муниципальное бюджетное общеобразовательное учреждение
«Гимназия №2 г. Торжка»
| ПРИНЯТО на заседании кафедрыПротокол № ___ от «_»___08_______2014г. Руководитель кафедры __________ В.Н.Чижова | СОГЛАСОВАНО на научно-методическом совете гимназии Протокол № ___от «__»____________2014 г. Зам. директора гимназии __________ | УТВЕРЖДАЮ Директор МБОУ «Гимназия №2»
___________
Приказ от г. № _____ |
РАБОЧАЯ ПРОГРАММА
по учебному предмету
«МАТЕМАТИКА»
11 класс
Разработана учителем математики
С.Д.Ушаковой
2014
Пояснительная записка
Сведения о программе
Учебный предмет математика состоит из двух предметных линий: алгебра и геометрия.
Рабочая программа по математике для 11класса создана на основе:
образовательной программы по математике среднего (полного) общего образования, утвержденной 08 августа 2012 года Приказ №101.
федерального компонента государственного стандарта среднего (полного)общего образования,
учебного плана гимназии.
федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях
учебных методических комплексов Е.П. Нелина, В.А. Лазарева, А.П.Ершова и С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева
2. Цели и задачи обучения математике
Изучение математики в 11 классе на базовом уровне направлено на достижение следующих целей:
формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
На основании требований Государственного образовательного стандарта 2004г. в содержании календарно-тематического планирования предполагается реализовать актуальные в настоящее время компетентностный, личностно-ориентированный, деятельностный подходы, которые определяют задачи обучения.При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа». В рамках указанных содержательных линий решаются следующие задачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;
расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;
систематическое изучение свойств геометрических тел в пространстве;
формирование умения применять полученные знания для решения практических задач;
формирование умения логически обосновывать выводы для изучения школьных естественнонаучных дисциплин на базовом уровне;
развитие способности к преодолению трудностей;
развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование интеллектуальных и речевых умений путем обогащения математического языка.
освоение компетенций: учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, ценностно-ориентационной и профессионально-трудового выбора
В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
Место предмета в федеральном базисном учебном плане.
Согласно учебному плану гимназии на изучение математики в 11 классе отводится 5 часов в неделю за счет федерального компонента - всего 170 часов, в том числе на изучение курса алгебры – 102 часа (3 часа в неделю), геометрии – 68 часов (2 часа в неделю)
На проведение контрольных работ – 10работ: 6 работ по алгебре и 4 работы по геометрии
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА МАТЕМАТИКА, 11 КЛАСС (АЛГЕБРА)
| № п/п | Тема | Содержание | Количество часов | Планируемый предметный результат | Контроль уровня обучения |
-
| Производная и её применение | Предел функции на бесконечности и в точке. Понятие о непрерывности функции. Приращение аргумента, приращение функции. Определение производной: задачи, приводящие к понятию производной, определение производной, ее геометрический и физический смысл, алгоритм отыскания производной. Вычисление производных: формулы дифференцирования для функций у = С, у = kx+m, y = x, y = 1/x, y =√x, y = sin x, y = cos x), правила дифференцирования (суммы, произведения, частного), дифференцирование функций y = x ³, y = tg x, y = ctg x, y = xª , дифференцирование функции y = f (kx + m). Уравнение касательной к графику функции. Применение производной для исследования функций: исследование функций на монотонность, отыскание точек экстремума, построение графиков функций. Отыскание наибольших и наименьших значений непрерывной функции на промежутке, задачи на отыскание наибольших и наименьших значений величин. | 36 | Знать, понимать: понятие производной, формулу производной степенной функции, формулы производных тригонометрических функций, правила дифференцирования, уравнение касательной, понятие точек экстремума функции, понятие наибольшего и наименьшего значений функции, схему исследования функции на монотонность и экстремумы Уметь находить производную степенной функции, пользуясь таблицей производных. находить производные тригонометрических функций. находить производные функций, пользуясь правилами дифференцирования. применять производную для исследования функций находить производную сложной функции применять производную для отыскания наибольшего и наименьшего значений функции находить угловой коэффициент касательной составлять уравнение касательной к графику функции в заданной точке
| Контрольная работа № 1 по теме «Производная» Контрольная работа № 2 по теме «Применение производной»
|
-
| Интеграл и его применение. | Определение первообразной. Основное свойство первообразной. Правила нахождения первообразных. Определенный интеграл, его геометрический и физический смысл. Формула Ньютона-Лейбница. Вычисление площадей плоских фигур с помощью первообразной.
| 14
| Знать: понятие первообразной, формулы для отыскания первообразных, правила отыскания первообразных; определение неопределенного интеграла, таблицу основных неопределенных интегралов, правила интегрирования понятие определенного интеграла, геометрический и физический смысл определенного интеграла, формулу Ньютона-Лейбница. Уметь: находить множество первообразных для заданной функции, находить первообразную, график которой проходит через заданную точку, находить неопределенный интеграл, используя правила интегрирования и таблицу основных неопределенных интегралов вычислять определенный интеграл, вычислять площади плоских фигур с помощью определенного интеграла | Контрольная работа №3 по теме:« Интеграл и его применение»
|
-
| Элементы комбинаторики и теории вероятности и статистики | Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля. Элементарные и сложные события. Понятие о вероятности события. Вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов | 20 | Знать понятия: вероятность событий, геометрическая вероятность, равновозможные исходы, предельный переход обработка информации, таблицы распределения данных, графики распределения данных, паспорт данных, числовые характеристики, таблица распределения, частота варианты, гистограмма распределения, мода, медиана, среднее ряда данных. определение относительной частоты случайного события. Уметь: формулировать классическое определение вероятности случайного события вычислять вероятность события вычислять относительную частоту события | Контрольная работа №4 по теме: «Элементы комбинаторики и теории вероятности и статистики»
|
-
| Комплексные числа | Множество комплексных чисел. Геометрическая интерпретация комплексного числа. Алгебраическая и тригонометрическая запись комплексного числа. | 10 | Знать: понятие комплексного числа, его модуля и аргумента правила действий над комплексными числами в алгебраической и тригонометрической формах Уметь: сумму, разность, произведение и частное комплексных чисел, степень комплексного числа и корень из комплексного числа | Контрольная работа №5 по теме: «Комплексные числа» |
-
| Ситематизация и обобщение сведений об уравнениях, неравенствах и их системах | Методы решения уравнений с одной переменной (равносильные преобразования, использование уравнений – следствий, применение свойств функций) Методы решения неравенств с одной переменной. Системы неравенств. Системы уравнений и методы их решения | 10 | Знать: Уметь: | Контрольная работа №6 по теме: «Методы решения уравнений, неравенств и их систем» |
-
| Итоговое повторение курса алгебры и начал математического анализа. Решение задач. | Решение рациональных и иррациональных уравнений. Решение показательных и логарифмических уравнений и их систем. Решение тригонометрических уравнений. Решение задач с использованием производной. Функция, определение, способы задания, свойства функций, сведенные в общую схему исследования функции, линейная функция, функция 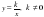 , квадратичная, показательная, логарифмическая функции, их свойства и график. Тригонометрические функции, их свойства и графики. Решение задач с использованием свойств функции. Тождественные преобразования степеней с рациональным показателем, иррациональных и логарифмических, тригонометрических выражений. , квадратичная, показательная, логарифмическая функции, их свойства и график. Тригонометрические функции, их свойства и графики. Решение задач с использованием свойств функции. Тождественные преобразования степеней с рациональным показателем, иррациональных и логарифмических, тригонометрических выражений.
| 10
| Уметь : выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; проводить по известным формулам и правилам преобразования буквенных выражений, включающих тригонометрические функции; вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; определять значение функции по значению аргумента при различных способах задания функции; строить графики изученных функций; описывать по графику и в простейших случаяхпо формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения; решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа |
|
-
| Резерв |
| 2 |
|
|
СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА МАТЕМАТИКА, 11 КЛАСС (геометрия)
| № п/п | Тема | Содержание | Количество часов | Планируемый предметный результат | Контроль уровня обучения |
-
| Метод координат в пространстве | Прямоугольная система координат в пространстве. Координаты вектора. Связь между координатами вектора и координатами точек. Угол между векторами. Скалярное произведение векторов. Углы между прямыми и плоскостями. Центральная, осевая и зеркальная симметрии, параллельный перенос. | 15
| Знать: понятие прямоугольной системы координат в пространстве, формулу разложения произвольного вектора по трем координатным векторам; понятие координат вектора в данной системе координат; понятие радиус-вектора произвольной точки пространства, доказательство утверждения, что координаты точки равны соответствующим координатам её радиус вектора, а координаты любого вектора равны разностям соответствующих координат его конца и начала; формулы координат середины отрезка, длины вектора через его координаты и расстояния между двумя точками понятие угла между векторами и скалярного произведения векторов, формулу скалярного произведения в координатах и свойства скалярного произведения; понятие движения пространства, основные виды движений Уметь: строить точку по заданным её координатам и находить координаты точки, изображенной в заданной системе координат; выполнять действия над векторами с заданными координатами; доказывать утверждение, что координаты точки равны соответствующим координатам её радиус вектора, а координаты любого вектора равны разностям соответствующих координат его конца и начала; применять изученный теоретический материал при решении задач вычислять скалярное произведение векторов и находить угол между векторами по их координатам; решать задачи на вычисление углов между двумя прямыми, между прямой и плоскостью доказать, что центральная, осевая, зеркальная симметрии и параллельный перенос являются движениями | Контрольная работа №1 по теме «Метод координат в пространстве»
|
-
| Цилиндр, конус, шар | Цилиндр, площадь поверхности цилиндра. Конус, площадь поверхности конуса. Сфера и шар. Уравнение сферы, взаимное расположение сферы и плоскости. Касательная плоскость к сфере. Площадь сферы | 20 | Знать: понятия цилиндрической поверхности, определение цилиндра, его элементы (боковая поверхность, основания, образующие, ось, высота, радиус); формулы для вычисления площадей боковой и полной поверхностей цилиндра понятия конической поверхности, определение конуса, его элементы (боковая поверхность, основание, вершина, образующие, ось, высота), усеченного конуса; формулы для вычисления площадей боковой и полной поверхностей конуса и усеченного конуса определения сферы, шара, понятие уравнения поверхности в пространстве, уравнение сферы Уметь: применять изученные формулы для решения задач по данной теме
| Контрольная работа №2 по теме «Тела вращения и их поверхности»
|
-
| Объемы тел | Понятие объема. Объем прямоугольного параллелепипеда. Объем прямой призмы. Объем цилиндра. Вычисление объемов с помощью интеграла. Объем наклонной призмы. Объем пирамиды. Объем конуса. Объем шара, шарового сегмента, слоя и сектора. Площадь сферы | 23
| Знать: единицы измерения объемов, свойства объемов; формулу объема куба и прямоугольного параллелепипеда формулы объемов прямой призмы и цилиндра формулы объемов наклонной призмы, пирамиды и конуса. формулы объема шара и площади сферы, шарового сегмента, шарового слоя и шарового сектора. формулы объема шара и площади сферы, шарового сегмента, шарового слоя и шарового сектора. Уметь: применять изученные формулы для решения задач по данной теме | . Контрольная работа №3 по теме «Объемы тел вращения» Контрольная работа № 4 по теме «Объемы тел и многогранников»
|
-
| Повторение | Взаимное расположение прямых и плоскостей. Многогранникии площади их поверхностей. Объемы тел. Сечения и их площади | 8 | Уметь распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями; анализировать в простейших случаях взаимное расположение объектов в пространстве; изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач; строить простейшие сечения куба, призмы, пирамиды; решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов) |
|
-
| Резерв |
| 2 |
|
|
КРИТЕРИИ И НОРМЫ ОЦЕНКИ ЗНАНИЙ, УМЕНИЙ И НАВЫКОВ УЧАЩИХСЯ ПО МАТЕМАТИКЕ
Оценивание знаний и умений проводится с учетом индивидуальных особенностей учащихся.
Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала выявляется полнота, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях. При оценке письменных и устных ответов учитель в первую очередь учитывает показанные учащимися знания и умения. Оценка зависит также от наличия и характера погрешностей, допущенных учащимися. Среди погрешностей выделяются ошибки и недочеты. Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе. К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в программе основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения; неаккуратная запись; небрежное выполнение чертежа.
Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач. Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью. Решение задачи считаемся безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
Оценка ответа учащихся при устном и письменном опросе проводится по пятибалльной системе. Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося, за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им заданий.
Оценка устных ответов учащихся.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно без наводящих вопросов учителя.
Возможны одна- две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Отметка «4» ставится в следующих случаях::
в изложении допущены небольшие проблемы, не исказившие математическое содержание ответа;
допущены один- два недочета при освещении основного содержания ответа;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала;
имелись затруднения или допущены ошибки в определении понятии, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Оценка письменных работ.
Письменная работа по математике может состоять только из примеров, только из задач, быть комбинированной или представлять собой математический диктант, когда учащиеся записывают только ответы или тест, когда учащиеся отмечают правильный вариант ответа.
Письменная работа, содержащая только примеры. При оценивании письменной работы, включающей только примеры (при числе вычислительных действий не более 15) и имеющей целью проверку вычислительных навыков учащихся, Ставятся следующие отметки:
Оценка «5» ставится, если вся работа выполнена безошибочно.
Оценка «4» ставится, если в работе допущены 1-2 вычислительные ошибки.
Оценка «3» ставится, если в работе допущены 3-5 вычислительных ошибок.
Оценка «2» ставится, если в работе допущено более 5 вычислительных ошибок.
Письменная работа, содержащая только задачи. При оценке письменной работы, содержащей только задачи (2 или 3 задачи) и имеющей целью проверку умений решать задачи, ставятся следующие отметки:
Отметка «5» ставится, если все задачи решены без ошибок.
Отметка «4» ставится, если, нет ошибок в ходе решения задач, но допущены 1-2 вычислительные ошибки.
Отметка «3» ставится, если допущена хотя бы одна ошибка в ходе решения задачи независимо от того, две или три задачи содержит работа, и одна вычислительна ошибка или если вычислительных ошибок нет, но не решена одна задача.
Отметка «2» ставится, если допущены ошибки в ходе решения двух задач или допущена ошибка в ходе решения одной задачи и две вычислительные ошибки в других задачах.
Письменная комбинированная работа. Письменная комбинированная работа ставит своей целью проверку знаний, умений, навыков учащихся по всему материалу темы, четверти, полугодии, всего учебного года и содержит одновременно задачи, примеры и задания других видов. Ошибки, допущенные при выполнении этих видов заданий, относятся к вычислительным ошибкам.
При оценке комбинированной работы, состоящей из одной задачи, примеров и заданий других видов (не более 5), ставятся следующие отметки:
Отметка «5» ставится, если вся работа выполнена безошибочно.
Отметка «4» ставится, если в работе допущены 1-2 вычислительные ошибки.
Отметка «3» ставится, если в работе допущена ошибка в ходе решения задачи при правильном выполнении всех остальных заданий или допущены 3-4 вычислительные ошибки при отсутствии ошибок в ходе решения задачи.
Оценка «2» ставится, если допущена ошибка в ходе решения задачи и хотя бы одна вычислительная ошибка или при решении задачи и примеров допущено более 4 вычислительных ошибок.
При оценке письменной комбинированной работы, состоящей из двух задач и примеров, ставятся следующие отметки:
Отметка «5» ставится, если вся работа выполнена безошибочно.
Отметка «4» ставится, если в работе допущены 1-2 вычислительные ошибки.
Отметка «3» ставится, если в работе допущена ошибка в ходе решения одной из задач, при правильном, выполнении всех остальных заданий, или допущены 3-4 вычислительные ошибки при отсутствии ошибок в ходе решений задач.
Отметка «2» ставится, если допущены ошибки в ходе решения двух задач, или допущена ошибка в ходе решения одной из задач и 4 вычислительные ошибки, или допущено более 6 вычислительных ошибок.
Примечание. Наличие в работе недочетов (неправильное списывание данных, но верное выполнение задания, грамматические ошибки в написании математических терминов и общепринятых сокращений, неряшливое оформление работы, большое количество исправлений) ведет к снижению оценки на один балл, но не ниже «3».
Математический диктант. При оценке математического диктанта, включающего 12 или более арифметических действий, ставятся следующие отметки:
Отметка «5» ставится, если вся работа выполнена безошибочно.
Отметка «4» ставится, если выполнена неверно 1/5 часть примеров от их общего числа.
Отметка «3» ставится, если выполнена неверно 1/4 часть примеров от их общего числа.
Отметка «2» ставится, если выполнена неверно 1/2 часть примеров от их общего числа.
или все задания выполнены с ошибками.
Тестирование. Отметка за тест:
Отметка «5» ставится, если набранное количество баллов составляет 90-100% от общего максимального количества баллов.
Отметка «4» ставится, если набранное количество баллов составляет 77-89% от общего максимального количества баллов.
Отметка «3» ставится, если набранное количество баллов составляет 60-76% от общего максимального количества баллов.
Отметка «2» ставится, если набранное количество баллов составляет менее 60% от общего максимального количества баллов.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ОБУЧАЮЩИХСЯ
ПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ ОБУЧЕНИЯ
Алгебра
В результате изучения курса алгебры и начал анализа 11-го класса учащиесядолжны
Знать:
понятия предела функции в точке, предела последовательности и понятие производной; научить находить производные с помощью формул дифференцирования; научить записывать уравнение касательной, применять производную к исследованию свойств функций и построению графиков функций.
понятие интеграла и интегрирования, как операции, обратной дифференцированию; научить находить площадь криволинейной трапеции.
понятие вероятности случайного события; научить вычислять вероятность события, пользуясь ее определением и комбинаторными схемами.
понятие комплексного числа в алгебраической и тригонометрической формах; изображать число на комплексной плоскости; научить находить сумму, разность, произведение и частное комплексных чисел, степень комплексного числа и корень из комплексного числа
методы решения уравнений, неравенств и их систем (включая уравнения, неравенства и их системы с параметрами).
Уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
находить корни многочленов с одной переменной, раскладывать многочлены на множители;
проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций, выполнять преобразования графиков;
описывать по графику и по формуле поведение и свойства функций;
решать уравнения, системы уравнений, неравенства, используя свойства функций и их
вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных, используя справочные материалы;
исследовать функции и строить их графики с помощью производной,;
решать задачи с применением уравнения касательной к графику функции;
решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;
вычислять площадь криволинейной трапеции;
· решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля;
· вычислять, в простейших случаях, вероятности событий на основе подсчета числа исходов;
решать рациональные, показательные и логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;
изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
находить приближенные решения уравнений и их систем, используя графический метод;
решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;
Геометрия
В результате изучения геометрии на базовом уровне в 11классе ученик должен
Знать
Многогранники. Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная.призма. Правильная призма. Параллелепипед. Куб.
Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Треугольная пирамида. Правильная пирамида. Усеченная пирамида.
Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрий в окружающем мире. Сечения куба, призмы, пирамиды. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Тела и поверхности вращения. Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию. Шар и сфера, их сечения, касательная плоскость к сфере.
Объемы тел и площади их поверхностей. Понятие об объеме тела. Отношение объемов подобных тел.
Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы.
Координаты и векторы. Декартовы координаты в пространстве. Формула расстояния между двумя точками. Уравнения сферы и плоскости. Формула расстояния от точки до плоскости.
Векторы. Модуль вектора. Равенство векторов. Сложение векторов и умножение вектора на число. Угол между векторами. Координаты вектора. Скалярное произведение векторов.
Уметь
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
владеть компетенциями: учебно – познавательной, ценностно – ориентационной, рефлексивной, коммуникативной, информационной, социально – трудовой.
МЕТАпредметные РЕЗУЛЬТАТЫ ОБУЧЕНИЯ:
выполнение практических расчетов по формулам, включая формулы, содержащие тригонометрические функции, используя при необходимости справочные материалы и простейшие
описание с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
уметь работать с вычислительными устройствами;
решать прикладные задачи, в том числе социально-экономические и физические, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
ЛИЧНОСТНЫЕ РЕЗУЛЬТАТЫ ОБУЧЕНИЯ:
На основании требований Государственного образовательного стандарта в содержании календарно-тематического планирования предлагается реализовать актуальные в настоящее время компетентностныйподход.В результате изучения математики в 10классе учащимся предоставляются возможности для формирования следующих компетентностей:
Познавательная компетентность:
Уметь выполнять практические расчеты по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Личностная компетентность:
Самостоятельно анализировать свою работу, аргументировать свою точку зрения;
Самообразовательная компетентность:
Самостоятельно приобретать и применять знания в различных ситуациях;
Социальная компетентность
Уметь слушать и анализировать мнение других; работать в группах
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
(алгебра)
| № урока | Тема урока | Планируемый предметный результат | Виды текущего и итогового контроля | Дата |
| план | факт |
| ПРОИЗВОДНАЯ И ЕЁ ПРИМЕНЕНИЕ 36 часов |
-
| Действительные числа и их свойства | Знать: понятие целого, рационального и действительного числа, модуля действительного числа, свойства модуля; Уметь: решать простейшие уравнения и неравенства с модулем |
|
|
|
-
| Понятие предела функции в точке | Знать: понятие предела функции в точке, свойства предела функции, Уметь: находить предел функции в точке |
|
|
|
-
| Непрерывность функции. Метод интервалов решения неравенств. | Знать, понятие непрерывной функции в точке, на промежутке Уметь: решать неравенства методом интервалов |
|
|
|
-
| Непрерывность функции. Метод интервалов решения неравенств. | Знать: понятие непрерывной функции в точке, на промежутке Уметь: решать неравенства методом интервалов | Самостоятельная работа С1 |
|
|
-
| Асимптоты графика функции | Знать: понятие асимптоты, виды асимптот Уметь: находить асимптоты графиков простейших функций |
|
|
|
-
| Асимптоты графика функции | Знать: понятие асимптоты, виды асимптот Уметь: находить асимптоты графиков простейших функций | Самостоятельная работа С3 |
|
|
-
| Понятие приращения аргумента и приращения функции. Задачи, приводящие к понятию производной. Определение производной. | Знать определение приращения функции, производной функции в точке Уметь: определять приращение функции при приращении аргумента, мгновенную скорость |
|
|
|
-
| Производные некоторых элементарных функций | Знать: алгоритм нахождения производной Уметь: находить производные простейших функций по алгоритму |
|
|
|
-
| Геометрический и механический смысл производной. Уравнение касательной к графику функции у=f (х) | Знать: уравнение касательной к графику функции, геометрический и физический смысл производной Уметь: находить угловой коэффициент касательной к графику функции в заданной точке, уравнение касательной в заданной точке по заданной производной |
|
|
|
-
| Правила вычисления производных | Знать: формулы дифференцирования, правила дифференцирования. Уметь: находить производные суммы, разности, произведения, частного; производные основных элементарных функций. | Самостоятельная работа С4 |
|
|
-
| Производная сложной функции | Знать: правила дифференцирования сложной функции. Уметь: находить производные сложных функций. |
|
|
|
-
| Производные элементарных функций | Знать: формулы нахождения производных Уметь: находить производные функций, уравнение касательной в заданной точке |
|
|
|
-
| Производные элементарных функций | Знать: формулы нахождения производных Уметь: находить производные функций, уравнение касательной в заданной точке, решать простейшие уравнения и неравенства с производной. | Самостоятельная работа С5 |
|
|
-
| Решение упражнений на нахождение производной | Знать: Формулы дифференцирования, правила дифференцирования Уметь: находить производные функций, применять производную при решении физических и геометрических задач |
|
|
|
-
| Решение упражнений на нахождение производной | Знать: Формулы дифференцирования, правила дифференцирования Уметь: находить производные функций, применять производную при решении физических и геометрических задач | Самостоятельная работа С6 |
|
|
-
| Контрольная работа № 1 по теме «Производная» | Уметь: решать задачи на нахождение производной | К1 |
|
|
-
| Анализ контрольной работы. Монотонность и постоянство функции. Критические точки функции. | Знать: понятия возрастающей и убывающей функции на промежутке, условие постоянства функции, Уметь: исследовать простейшие функции на монотонность |
|
|
|
-
| Монотонность и постоянство функции. Критические точки функции. | Знать: понятия возрастающей и убывающей функции на промежутке, условие постоянства функции, Уметь: исследовать простейшие функции на монотонность |
|
|
|
-
| Экстремумы функции. Необходимое и достаточное условие экстремума | Знать: понятие точки экстремума, точки максимума и минимума, необходимое условие экстремума Уметь: исследовать простейшие функции на монотонность и на экстремумы |
|
|
|
-
| Экстремумы функции. Необходимое и достаточное условие экстремума | Знать: понятие точки экстремума, точки максимума и минимума, необходимое условие экстремума Уметь: исследовать показательные, логарифмические и степенные функции на монотонность и на экстремумы | Самостоятельная работа С8 |
|
|
-
| Решение упражнений на нахождение промежутков монотонности и экстремумов функции | Уметь: исследовать функции на монотонность и на экстремумы |
|
|
|
-
| Решение упражнений на нахождение промежутков монотонности и экстремумов функции | Уметь: исследовать функции на монотонность и на экстремумы | Самостоятельная работа С9 |
|
|
-
| Общая схема исследования функции для построения ее графика | Знать: общую схему исследования функции Уметь: пользуясь планом, исследовать функцию |
|
|
|
-
| Решение упражнений на исследование функций с помощью производной и построение графиков функций | Уметь: пользуясь планом, исследовать функцию и построить её график. |
|
|
|
-
| Решение упражнений на исследование функций с помощью производной и построение графиков функций | Уметь: пользуясь планом, исследовать функцию и построить её график. |
|
|
|
-
| Решение упражнений на исследование функций с помощью производной и построение графиков функций | Уметь: пользуясь планом, исследовать функцию и построить её график. | Домашняя практическая работа С10 |
|
|
-
| Нахождение наибольшего и наименьшего значения функций | Знать: алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на промежутке, алгоритм нахождения наименьшего и наибольшего значений непрерывной функции на отрезке Уметь: находить наибольшие и наименьшие значения функций |
|
|
|
-
| Нахождение наибольшего и наименьшего значения функций | Знать: алгоритм нахождения наибольшего и наименьшего значений непрерывной функции на промежутке, алгоритм нахождения наименьшего и наибольшего значений непрерывной функции на отрезке Уметь: находить наибольшие и наименьшие значения функций | Самостоятельная работа С11 |
|
|
-
| Решение задач на применение производной к исследованию функций | Уметь: применять производную к исследованию свойств функций и построению графиков функций. |
|
|
|
-
| Решение задач на применение производной к исследованию функций | Уметь: применять производную к исследованию свойств функций и построению графиков функций. | Домашняя самостоятельная работа С12 |
|
|
-
| Решение задач на применение производной к исследованию функций | Уметь: применять производную к исследованию свойств функций и построению графиков функций. |
|
|
|
-
| Контрольная работа № 2 по теме «Применение производной» | Уметь: применять производную к исследованию свойств функций и построению графиков функций, решать прикладные задачи на применение производной | К2 |
|
|
-
| Анализ контрольной работы. Применение производной к решению уравнений и неравенств | Уметь: решать уравнения с помощью оценки левой и правой частей и возрастания или убывания функции |
|
|
|
-
| Применение производной к доказательству неравенств | Уметь: применять производную к доказательству неравенств |
|
|
|
-
| Применение производной к решению задач с параметрами | Уметь: решать простейшие задачи с параметрами для исследования функции на монотонность, экстремумы, записи уравнений касательных. |
|
|
|
-
| Применение производной к решению задач с параметрами | Уметь: решать простейшие задачи с параметрами для исследования функции на монотонность, экстремумы, записи уравнений касательных. | Самостоятельная работа С15 |
|
|
| ИНТЕГРАЛ И ЕГО ПРИМЕНЕНИЕ 14 часов |
-
| Понятие первообразной. Основное свойство первообразных. Неопределенный интеграл. | Знать: понятии первообразной, неопределенного интеграла, свойства первообразной. Уметь находить первообразные. |
|
|
|
-
| Правила нахождения первообразных. Таблица первообразных. | Знать понятие первообразной суммы, разности. Уметь: вычислить первообразную от суммы, разности функций; вычислять первообразную от функции с множителем |
|
|
|
-
| Правила нахождения первообразных. Таблица первообразных. | Знать понятие первообразной суммы, разности. Уметь: вычислить первообразную от суммы, разности функций; вычислять первообразную от функции с множителем | Самостоятельная работа С16 |
|
|
-
| Геометрический смысл и определения определенного интеграла. Формула Ньютона – Лейбница. | Знать формулу Ньютона - Лейбница. Уметь вычислять определенный интеграл по формуле Ньютона - Лейбница |
|
|
|
-
| Геометрический смысл и определения определенного интеграла. Формула Ньютона – Лейбница. | Знать формулу Ньютона - Лейбница. Уметь вычислять определенный интеграл по формуле Ньютона - Лейбница |
|
|
|
-
| Свойства определенных интегралов. Определение определенного интеграла через интегральные суммы. | Знать: свойства определенных интегралов, определение определенного интеграла через интегральные суммы. Уметь: вычислять определенный интеграл |
|
|
|
-
| Свойства определенных интегралов. Определение определенного интеграла через интегральные суммы. | Знать: свойства определенных интегралов, определение определенного интеграла через интегральные суммы. Уметь: вычислять определенный интеграл |
|
|
|
-
| Решение упражнений на нахождение определенных интегралов | Уметь: вычислять площадь фигуры, ограниченной линиями |
|
|
|
-
| Решение упражнений на нахождение определенных интегралов | Уметь: вычислять площадь фигуры, ограниченной линиями |
|
|
|
-
| Вычисление площадей плоских фигур | Уметь: вычислять площадь криволинейной трапеции |
|
|
|
-
| Вычисление площадей плоских фигур | Уметь: вычислять площадь криволинейной трапеции | Самостоятельная работа С17 |
|
|
-
| Вычисление объемов тел | Уметь: вычислять объем тела, полученного вращением криволинейной трапеции вокруг оси абсцисс |
|
|
|
-
| Решение упражнений на нахождение и применение определенных интегралов | Уметь решать задачи на применение интегралов | Домашняя самостоятельная работа С19 |
|
|
-
| Контрольная работа №3 по теме: «Интеграл и его применение» | Уметь решать задачи на нахождение и применение интегралов | К3 |
|
|
| ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, ТЕОРИИ ВЕРОЯТНОСТЕЙ И СТАТИСТИТКИ 20 часов |
-
| Анализ контрольной работы Понятие соединения. Правило суммы и произведения. Упорядоченные множества. Размещение. | Знать определения соединения, размещения. Правило суммы и произведения. Уметь: размещение из п элементов по к |
|
|
|
-
| Перестановки | Иметь представление о перестановках Уметь: решать задачи на перестановки. |
|
|
|
-
| Сочетания | Иметь представление о сочетании. Уметь решать простейшие задачи на сочетание. | Самостоятельная работа С20 |
|
|
-
| Вычисление числа сочетаний без повторений с помощью треугольника Паскаля. | Уметь вычислять число сочетаний из п элементов по кс помощью треугольника Паскаля. |
|
|
|
-
| Решение комбинаторных задач | Уметь решать простейшие комбинаторные задачи | Самостоятельная работа С21 |
|
|
-
| Бином Ньютона | Знать формулу бинома Ньютона Уметь применять формулу для разложения многочлена на множители |
|
|
|
-
| Бином Ньютона | Знать формулу бинома Ньютона Уметь применять формулу для разложения многочлена на множители | Самостоятельная работа С22 |
|
|
-
| Понятие случайного события и случайного эксперимента. Классическое определение вероятности | Иметь представление о достоверных событиях, о невозможном и случайном событии, о стопроцентной и нулевой вероятности, о равновероятностных событиях, классическое определение вероятности Уметь осуществлять проверку выводов, положений, закономерностей |
|
|
|
-
| Понятие случайного события и случайного эксперимента. Классическое определение вероятности | Иметь представление о достоверных событиях, о невозможном и случайном событии, о стопроцентной и нулевой вероятности, о равновероятностных событиях, классическое определение вероятности Уметь осуществлять проверку выводов, положений, закономерностей | Самостоятельная работа С24 |
|
|
-
| Операции над событиями | Знать определение противоположного события, суммы событий, произведения событий, несовместных событий Уметь находить их вероятность | Самостоятельная работа С25 |
|
|
-
| Относительная частота случайного события. Статистическое определение вероятности. | Знать понятие частоты и относительной частоты случайного события, смысл статистического определения вероятности Уметь находить вероятность используя аксиомы. |
|
|
|
-
| Геометрическое определение вероятности | Знать определение геометрической вероятности | Самостоятельная работа С26 |
|
|
-
| Условные вероятности | Знать понятие условной вероятности, теорему умножения вероятностей Уметь: находить условную вероятность, вероятность произведения |
|
|
|
-
| Независимые события | Знать определение независимости двух событий Уметь находить вероятность произведения независимых событий |
|
|
|
-
| Понятие случайной величины и ее распределения. Математическое ожидание случайной величины. | Знать понятие случайной величины, закона распределения случайной величины Уметь находить математическое ожидание случайной величины. |
|
|
|
-
| Понятие о статистике. Генеральная совокупность и выборка. | Знать понятие генеральной совокупности, выборки, репрезентативной выборки |
|
|
|
-
| Табличное и графическое представление данных. Числовые характеристики рядов данных | Знать понятие полигона частот, размаха, моды и среднего значения Уметь решать задачи на нахождение размаха, моды и среднего значения |
|
|
|
-
| Табличное и графическое представление данных. Числовые характеристики рядов данных | Знать понятие полигона частот, размаха, моды и среднего значения Уметь решать задачи на нахождение размаха, моды и среднего значения | Самостоятельная работа С28 |
|
|
-
| Решение комбинаторных задач | Уметь решать комбинаторные задачи. |
|
|
|
-
| Контрольная работа №4 по теме: «Элементы комбинаторики и теории вероятности и статистики» | Уметь решать комбинаторные задачи. | К4 |
|
|
| КОМПЛЕКСНЫЕ ЧИСЛА 10 часов |
-
| Анализ контрольной работы. Множество комплексных чисел. Алгебраическая форма комплексного числа. | Знать понятие комплексного числа, равных комплексных чисел |
|
|
|
-
| Действия над комплексными числами в алгебраической форме. | Знать понятие суммы, разности, произведения и частного равных комплексных чисел Уметь находить сумму, разность, произведение и частное равных комплексных чисел |
|
|
|
-
| Действия над комплексными числами в алгебраической форме. | Знать понятие суммы, разности, произведения и частного равных комплексных чисел Уметь находить сумму, разность, произведение и частное равных комплексных чисел | Самостоятельная работа С29 |
|
|
-
| Геометрическое изображение комплексных чисел | Уметь изображать комплексные числа на координатной плоскости | Самостоятельная работа С30 |
|
|
-
| Тригонометрическая форма комплексного числа | Знать понятие модуля и аргумента комплексного числа, общий вид комплексного числа в тригонометрической форме Уметь представлять комплексное число в тригонометрической форме |
|
|
|
-
| Тригонометрическая форма комплексного числа | Знать понятие модуля и аргумента комплексного числа, общий вид комплексного числа в тригонометрической форме Уметь представлять комплексное число в тригонометрической форме |
|
|
|
-
| Действия над числами, записанными в тригонометрической форме | Уметь выполнять действия над числами, записанными в тригонометрической форме | Самостоятельная работа С31 |
|
|
-
| Действия над числами, записанными в тригонометрической форме | Уметь выполнять действия над числами, записанными в тригонометрической форме |
|
|
|
-
| Решение уравнений с комплексными корнями | Уметь решать уравнения с комплексными корнями | Домашняя самостоятельная работа С32 |
|
|
-
| Контрольная работа №5 по теме: «Комплексные числа» | Уметь выполнять действия с комплексными числами в различных формах | К5 |
|
|
| СИСТЕМАТИЗАЦИЯ И ОБОБЩЕНИЕ СВЕДЕНИЙ ОБ УРАВНЕНИЯХ, НЕРАВЕНСТВАХ И ИХ СИСТЕМАХ 10 часов |
-
| Анализ контрольной работы. Методы решения уравнений с одной переменной
| Знать понятие ОДЗ, решения, равносильности уравнений, основные методы решения уравнений Уметь решать различные виды уравнений изученными методами. |
|
|
|
-
| Методы решения уравнений с одной переменной Повторение. Тригонометрические, степенные уравнения | Знать понятие ОДЗ, решения, равносильности уравнений, основные методы решения уравнений Уметь решать различные виды уравнений изученными методами. |
|
|
|
-
| Методы решения неравенств с одной переменной Повторение. Тригонометрические, степенные неравенства | Знать понятие ОДЗ, решения, равносильности неравенств, основные методы решения уравнений Уметь решать различные виды неравенств изученными методами. |
|
|
|
-
| Методы решения неравенств с одной переменной Повторение. Тригонометрические, степенные неравенства | Знать понятие ОДЗ, решения, равносильности неравенств, основные методы решения уравнений Уметь решать различные виды неравенств изученными методами. |
|
|
|
-
| Методы решения систем уравнений и неравенств с одной переменной. Повторение Иррациональные уравнения и неравенства | Знать понятие ОДЗ, решения, равносильности систем уравнений, основные методы решения уравнений Уметь решать различные виды систем уравнений изученными методами. |
|
|
|
-
| Методы решения систем уравнений и неравенств с одной переменной Повторение логарифмические уравнения и неравенства | Знать понятие ОДЗ, решения, равносильности систем уравнений, основные методы решения уравнений Уметь решать различные виды систем уравнений изученными методами. | Самостоятельная работа С33 |
|
|
-
| Задачи с параметрами. | Уметь решать простейшие исследовательские задачи с параметрами |
|
|
|
-
| Задачи с параметрами | Уметь решать простейшие исследовательские задачи с параметрами | Самостоятельная работа С34 |
|
|
-
| Задачи с параметрами | Уметь решать простейшие исследовательские задачи с параметрами |
|
|
|
-
| Контрольная работа №6 по теме: «Методы решения уравнений, неравенств и их систем» | Уметь решать уравнения, неравенства и системы уравнений и неравенств | К6 |
|
|
| ИТОГОВОЕ ПОВТОРЕНИЕ 12 часов |
-
| Анализ контрольной работы. Основные тригонометрические формулы |
|
|
|
|
-
| Тригонометрические функции |
|
|
|
|
-
| Степенная функция |
|
|
|
|
-
| Показательная и логарифмическая функции |
|
|
|
|
-
| Разбор задач открытого банка данных ЕГЭ часть В: текстовые задачи |
|
|
|
|
-
| Разбор задач открытого банка данных ЕГЭ часть В текстовые задачи |
|
|
|
|
-
| Разбор задач открытого банка данных ЕГЭ часть В:производная и ее применение |
|
|
|
|
-
| Разбор задач открытого банка данных ЕГЭ часть В |
|
|
|
|
-
| Тестирование в формате ЕГЭ |
|
|
|
|
-
| Тестирование в формате ЕГЭ |
|
|
|
|
-
| Резерв |
|
|
|
|
-
| Резерв |
|
|
|
|
| Геометрия |
| Метод координат в пространстве 15 часов |
|
|
-
| Прямоугольная система координат в пространстве | Иметь представление о прямоугольной системе координат в пространстве. Уметь строить точку по заданным координатам и находить координаты точки, изображенной в заданной системе координат. |
|
|
|
-
| Координаты вектора | знать разложение вектора по координатным векторам; Уметьвыполнять действия над векторами с заданными координатами | самостоятельная работа |
|
|
-
| Связь между координатами векторов и координатами точек | Знать определение радиус- вектора произвольной точки пространства; Уметь находить координаты вектора по координатам его начала и конца |
|
|
|
-
| Простейшие задачи в координатах | Знать формулы координат середины отрезка,длины вектора через его координаты и расстояния между двумя точками. Уметь применять эти формулы при решении стереометрических задач. | математический диктант |
|
|
-
| Угол между векторами. Скалярное произведение векторов | Знать понятие угла между векторами и скалярного произведения векторов; знать формулу скалярного произведения в координатах, свойства скалярного произведения. Уметь применять скалярное произведение при решении задач. |
|
|
|
-
| Свойства скалярного произведения. Скалярное произведение в координатах. | Уметь применять скалярное произведение при решении задач. |
|
|
|
-
| Вычисление углов между прямыми и плоскостями | Знать понятие угла между векторами и скалярного произведения векторов. Знать формулу скалярного произведения в координатах, косинуса угла между данными векторами через их координаты, косинуса угла между прямыми, между прямой и плоскостью.Уметь использовать скалярное произведение векторов при решении задач на вычисление углов между рямыми, между прямой и плоскостью. |
|
|
|
-
| Решение задач на применение скалярного произведения векторов. | Уметь использовать скалярное произведение векторов при решении задач на вычисление углов между рямыми, между прямой и плоскостью. | самостоятельная работа |
|
|
-
| Движение. Центральная симметрия. Осевая симметрия . | Иметь понятие о движении в пространстве, знать основные виды движений, их свойства |
|
|
|
-
| Зеркальная симметрия в пространстве. Параллельный перенос в пространстве. | Уметь осуществлять виды движений; находить координаты точек при различных движениях. |
|
|
|
-
| Векторный метод решения задач. | Уметь:выполнять действия над векторами, решать стереометрические задачи координатно-векторным методом, строить образы геометрических фигур при симметриях, параллельном переносе, повороте. |
|
|
|
-
| Применение векторного метода для многогранников | Уметь применять скалярное произведение при решении задач. |
|
|
|
-
| Применение векторного метода для нахождения углов между прямыми и плоскостями. | Уметь использовать скалярное произведение векторов при решении задач на вычисление углов между рямыми, между прямой и плоскостью. |
|
|
|
-
| Виды движений в решении задач. | Иметь понятие о движении в пространстве, знать основные виды движений, их свойства Уметь осуществлять виды движений; находить координаты точек при различных движениях. |
|
|
|
-
| Контрольная работа №1 по теме «Метод координат в пространстве» | уметь применять знания по теме «Метод координат в пространстве». | Контрольная работа |
|
|
| Цилиндр, конус, шар (20 ч) |
|
|
-
| Анализ к.р. Цилиндр, цилиндрическое сечение и свойства | Знать:понятия цилиндрической поверхности, определение цилиндра, его элементы (боковая поверхность, основания, образующие, ось, высота, радиус); формулы для вычисления площадей боковой и полной поверхностей цилиндраУметь:применять изученные формулы для решения задач по данной теме |
|
|
|
-
| Решение задач на определение длин частей цилиндра. | Уметь:применять изученные формулы для решения задач по данной теме |
|
|
|
-
| Площадь поверхности цилиндра | Уметь:применять изученные формулы для решения задач по данной теме |
|
|
|
-
| Вписанный и описанный цилиндр | Уметь:применять изученные формулы для решения задач по данной теме | самостоятельная работа |
|
|
-
| Решение задач на применение формул площадей поверхности цилиндра | Уметь:применять изученные формулы для решения задач по данной теме |
|
|
|
-
| Конус, коническое сечение и его свойства | Знать:понятия конической поверхности, определение конуса, его элементы (боковая поверхность, основание, вершина, образующие, ось, высота), усеченного конуса |
|
|
|
-
| Решение задач на определение длин частей конуса | уметь решать задачи по теме | математический диктант |
|
|
-
| Площадь поверхности конуса | Знать:формулы для вычисления площадей боковой и полной поверхностей конуса и |
|
|
|
-
| Решение задач на применение формул площадей поверхности конуса | уметь применять формулы для вычисления площадей боковой и полной поверхностей конуса |
|
|
|
-
| Усеченый конус. Определения и свойства | Знать:понятия усеченного конуса; |
|
|
|
-
| Решение задач на усеченный конус | уметь решать задачи по теме |
|
|
|
-
| Сфера и шар . Сечения шара | Знатьопределения сферы, шара, Уметьрешать задачи |
|
|
|
-
| Части шара:сегмент, сектор, пояс | Знать основные понятия по теме |
|
|
|
-
| Теорема о касательной плоскости к сфере | Знать:свойство касательной к сфере, что собой представляет расстояние от центра сферы до плоскости сечения.Уметь:решать задачи по теме |
|
|
|
-
| Уравнение сферы. Вписанная и описанная сферы. | Знать определение сферы, шара, уравнение сферы в заданной прямоугольной системе координат;Уметь находить отдельные элементы сферы и шара, записывать уравнение сферы. |
|
|
|
-
| Площадь сферы | Знать:формулу площади сферы.Уметь: применять формулу при решении задач на нахождение площади сферы. |
|
|
|
-
| Площадь сферы | Знать:формулу площади сферы.Уметь: применять формулу при решении задач на нахождение площади сферы. |
|
|
|
-
| Комбинация тел вращения | Иметь представление о шаре (сфере) вписанном в многогранник, описанном около многогранника. Знать условия их существования. Уметь решать задачи на комбинацию тел вращения и многогранников |
|
|
|
-
| Комбинация тел вращения | Иметь представление о шаре (сфере) вписанном в многогранник, описанном около многогранника. Знать условия их существования. Уметь решать задачи на комбинацию тел вращения и многогранников |
|
|
|
-
| Контрольная работа №2 по теме «Тела вращения и их поверхности» | Знать:элементы цилиндра, конуса, уравнение сферы, формулы боковой и полной поверхностей; уметь решать задачи по теме | Контрольная работа |
|
|
| Объемы тел (23 ч) |
|
|
-
| Анализ к.р. Объем. Основные свойства объема | Знать: единицы измерения объемов, свойства объемов; |
|
|
|
-
| Объем прямоугольного параллелепипеда. | Знать:формулы объема прямоугольного параллелепипеда.Уметь:находить объем куба и объем прямоугольного параллелепипеда. |
|
|
|
-
| Решение задач на нахождение объемов параллелепипедов. | Уметь:находить объем куба и объем прямоугольного параллелепипеда |
|
|
|
-
| Решение задач на нахождение объемов параллелепипедов. | Уметь:находить объем куба и объем прямоугольного параллелепипеда | самостоятельная работа |
|
|
-
| Объем прямой призмы. Решение задач. | Знать:теорему об объеме прямой призмы.Уметь:решать задачи с использованием формулы объема прямой призмы |
|
|
|
-
| Объем цилиндра. Решение задач. | Знать:формулу объема цилиндраУметь: выводить формулу и использовать ее при решении задач | математический диктант |
|
|
-
| Вычисление объемов тел с помощью определенных интегралов. | Знать возможность и целесообразность применения определенного интеграла для вычисления объемов тел |
|
|
|
-
| Вычисление объемов тел с помощью определенных интегралов. | Знать возможность и целесообразность применения определенного интеграла для вычисления объемов тел |
|
|
|
-
| Объем наклонной призмы. | Знать:формулу объема наклонной примы.Уметь:находить объем наклонной призмы |
|
|
|
-
| Объем пирамиды. | Знать:метод вычисления объема через опре-деленный интеграл.Уметь:применять метод для вывода формулы объема пирамиды, находить объем пирамиды, находить объем пирамиды | самостоятельная работа |
|
|
-
| Объем конуса. | Знать:формулы объема конуса. Уметь: выводить формулы объемов конуса и усеченного конуса, решать задачи на вычисление объемов конуса и усеченного конуса |
|
|
|
-
| Решение различных задач на нахождение объемов тел. | Знать:формулы объемов.Уметь: решать простейшие стереометрические задачи на нахождение объемов |
|
|
|
-
| Решение различных задач на нахождение объемов тел. | Знать:формулы объемов.Уметь:решать простейшие стереометрические задачи на нахождение объемов |
|
|
|
-
| Контрольная работа №3 по теме «Объемы тел вращения» | Знать:формулы и уметь использовать их при решении задач | Контрольная работа |
|
|
-
| Анализ к.р. Объем шара. Вывод формулы. Решение задач. | Знать:формулу объема шара.Уметь: выводить формулу с помощью определенного интеграла и использовать ее при решении задач на нахождение объема шара. |
|
|
|
-
| Объем шара. | Знать:формулу объема шара.Уметь использовать формулу при решении задач на нахождение объема шара. | математический диктант |
|
|
-
| Объем шарового слоя и шарового сектора. | Иметь представление о шаровом сегменте, шаровом секторе, слое.Знать:формулу объемов этих тел.Уметь:решать задачи на нахождение объемов шарового слоя, сектора, сегмента |
|
|
|
-
| Площадь сферы и ее частей. Решение задач. | Знать:формулу площади сферы.Уметь: выводить формулу площади сферы, решать задачи на вычисление площади сферы |
|
|
|
-
| Площадь сферы и ее частей. Решение задач. | Знать:формулу площади сферы.Уметь: выводить формулу площади сферы, решать задачи на вычисление площади сферы |
|
|
|
-
| Решение комбинированных задач на объемы. | Использовать приобретенные знания и умения в практической деятельности для вычисления объема шара и площади сферы |
|
|
|
-
| Решение задач по теме « Объемы» | Использовать приобретенные знания и умения в практической деятельности для вычисления объема шара и площади сферы |
|
|
|
-
| Решение задач по теме « Объемы» | Использовать приобретенные знания и умения в практической деятельности для вычисления объема шара и площади сферы |
|
|
|
-
| Контрольная работа № 4 по теме «Объемы тел и многогранников» | Знать:формулы и уметь использовать их при решении задач | Контрольная работа |
|
|
| Повторение курса (10ч) |
|
|
-
| Анализ к.р. Многогранники | Знать формулы для вычисления площадей поверхностей многогранников. Уметь изображать многогранники;уметь использовать формулы при решении задач. |
|
|
|
-
| Многогранники | Знать формулы для вычисления площадей поверхностей многогранников. Уметь изображать многогранники;уметь использовать формулы при решении задач. |
|
|
|
-
| Взаимное расположение прямых и плоскостей | Знать взаимное расположение прямых и плоскостей |
|
|
|
-
| Площади поверхностей | Знать формулы площадей поверхностей; уметь решать задачи по теме |
|
|
|
-
| Объемы | Знать формулы для вычисления объемов тел. Уметь использовать полученные знания при решении задач. |
|
|
|
-
| Сечения | Уметь строить сечения и решать задачи |
|
|
|
-
| Решение комбинированных задач | Знать формулы для вычисления площадей поверхностей тел; формулы для вычисления объемов тел;уметь использовать формулы при решении задач. |
|
|
|
-
| Решение комбинированных задач | Знать формулы для вычисления площадей поверхностей тел; формулы для вычисления объемов тел; уметь использовать формулы при решении задач. |
|
|
|
-
| Решение комбинированных задач | Знать формулы для вычисления площадей поверхностей тел; формулы для вычисления объемов тел;уметь использовать формулы при решении задач. |
|
|
|
-
| Решение комбинированных задач | Знать формулы для вычисления площадей поверхностей тел; формулы для вычисления объемов тел;уметь использовать формулы при решении задач. |
|
|
|
УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПРОГРАММЫ
| Материально – техническое обеспечение | Основная литература | Учебные и справочные пособия | Учебно-методическая литература | Медиаресурсы |
| Компьютер Интерактивная доска, принтер | Е.П. Нелин, В.А. Лазарев Алгебра и начала математического анализа.11 класс. Учебник. – М.: Илекса Геометрия, 10–11: Учеб.дляобщеобразоват. учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение,
| Е.П. Нелин, А.П.Ершова. Алгебра 7-11 классы. Определения, свойства и методы решения задач - в таблицах. – М.: Илекса Г.В. Дорофеев, Г.К. Муравин, Е.А. Седова Сборник заданий для подготовки и проведения письменного экзамена по математике (курс А) и алгебре и началам анализа (курс В) за курс средней школы. 11 кл. М.,Дрофа,; Ф.Ф. Лысенко Математика ЕГЭ –. Учебно-тренировочные тесты. – Ростов-на-Дону: Легион; Ф.Ф. Лысенко Тематические тесты. Математика ЕГЭ – Ростов-на-Дону: Легион;
| Е.П. Нелин, В.А. Лазарев Программы образовательных учреждений. Алгебра и начала математического анализа.10-11классы.. – М.: Илекса Е.П. Нелин, В.А. Лазарев, А.П.Ершова. Книга для учителя. – М.: Илекса Е.П. Нелин, А.П.Ершова. Самостоятельные и контрольные работы по алгебре и началамматематическогоанализа.11 класс. – М.: Илекса Е.П. Нелин, А.П.Ершова. Тематические и итоговые тесты. М.: Илекса Математика. Тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного и вступительного экзаменов / сост. Г.И. Ковалева, Т.И. Бузулина, О.Л. Безрукова, Ю.А. Розка – Волгоград: Учитель,; Ивлев Б.И., Саакян С.И., Шварцбург С.И., Дидактические материалы по алгебре и началам анализа для 11 класса, М.,; Шамшин В.М. Тематические тесты для подготовки к ЕГЭ по математике, Феникс, Ростов-на-Дону, Студенецкая В.Н. Математика: система подготовки учащихся к ЕГЭ, Волгоград,; Математика. Еженедельное приложение к газете «Первое сентября»; Математика в школе. Ежемесячный научно-методический журнал.
| Министерство образования РФ: http://www.informika.ru/; http://www.ed.gov.ru/ ; http://www.edu.ru/ Тестирование online: 5 - 11 классы : http://www.kokch.kts.ru/cdo/ Педагогическая мастерская, уроки в Интернет и многое другое: http://teacher.fio.ru Новые технологии в образовании: http://edu.secna.ru/main/ Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru сайты «Энциклопедий»: http://www.rubricon.ru/ ; http://www.encyclopedia.ru/ |
ГРАФИК КОНТРОЛЬНЫХ РАБОТ
| №п/п | Тема | Дата проведения |
| Контрольная работа № 1 по теме «Производная» |
|
| Контрольная работа № 2 по теме «Применение производной» |
|
| Контрольная работа №3 по теме:« Интеграл и его применение» |
|
| Контрольная работа №4 по теме: «Элементы комбинаторики и теории вероятности и статистики» |
|
| Контрольная работа №5 по теме: «Комплексные числа» |
|
| Контрольная работа №6 по теме: «Методы решения уравнений, неравенств и их систем» |
|
| Контрольная работа №1 по теме «Метод координат в пространстве» |
|
| Контрольная работа №2 по теме «Тела вращения и их поверхности» |
|
| . Контрольная работа №3 по теме «Объемы тел вращения» |
|
| Контрольная работа № 4 по теме «Объемы тел и многогранников» |
|

 Получите свидетельство
Получите свидетельство Вход
Вход


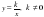 , квадратичная, показательная, логарифмическая функции, их свойства и график. Тригонометрические функции, их свойства и графики. Решение задач с использованием свойств функции. Тождественные преобразования степеней с рациональным показателем, иррациональных и логарифмических, тригонометрических выражений.
, квадратичная, показательная, логарифмическая функции, их свойства и график. Тригонометрические функции, их свойства и графики. Решение задач с использованием свойств функции. Тождественные преобразования степеней с рациональным показателем, иррациональных и логарифмических, тригонометрических выражений. 








 Рабочая программа по математике для 11 класса (0.1 MB)
Рабочая программа по математике для 11 класса (0.1 MB)
 1
1 585
585 33
33 Нравится
0
Нравится
0


