Рабочая программа по математике для 1-х классов

Рабочая программа «Математика» Чекина А. Л. и (образовательная программа «Перспективная начальная школа») разработана на основе Федерального государственного образовательного стандарта начального общего образования, основных положений развивающей личностно-ориентированной системы «Перспективная начальная школа», реализующей межпредметные и внутрипредметные связи, логику учебного процесса, задачи формирования у младшего школьника умения учиться. 

УМК «Перспективная начальная школа», 2011 г., учебник Чекина А. Л. (Москва, Академкнига/Учебник, 2011г. ) Курс рассчитан на 132 часа (4 часа в неделю).

Программу обеспечивают:

Чекин А. Л. Математика. 1 класс: Учебник. В 2 ч. — М. : Академкнига/ Учебник.

Юдина Е. П. Математика: Тетради для самостоятельной работы №1, №2. — М. ; Академкнига/Учебник.

Чекин А. Л. Математика: Методическое пособие для учителя. В 2 ч. — М. : Академкнига/Учебник.

Цель:

ввести ребенка в абстрактный мир математических понятий и их свойств, охватывающих весь материал обязательного минимума начального математического образования и дать первоначальные навыки ориентации в той части реальной действительности, которая описывается (моделируется) с помощью этих понятий, а именно: окружающий мир как множество форм, как множество предметов, отличающихся величиной, которую можно выразить числом как разнообразие классов конечных равночисленных множеств и т. п., а также предложить ребенку соответствующие способы познания окружающей действительности.

Задачи:

- овладение знаниями и умениями, необходимыми для успешного решения учебных и практических задач и продолжения образования;

- развитие личности ребенка, и прежде всего его мышления как основы развития других психических процессов: памяти, внимания, воображения, математической речи и способностей;

- формирование основ общих учебных умений и способов деятельности, связанных с методами познания окружающего мира (наблюдения, измерения, моделирования), приемов мыслительной деятельности (анализ, синтез, сравнение, классификация, обобщение), способов организации учебной деятельности (планирование, самоконтроль, самооценка и др. ).

Основная дидактическая идея курса может быть выражена следующей формулой: через рассмотрение частного к пониманию общего для решения частного. При этом ребенку предлагается постичь суть предмета через естественную связь математики с окружающим миром.

Отличительной чертой настоящего курса является значительное увеличение изучения геометрического материала и изучения величин. Изучение же арифметического материала, оставаясь стержнем всего курса, осуществляется с возможным паритетом теоретической и прикладной составляющих, а в вычис­лительном плане особое внимание уделяется способам и технике устных вычислений.

Общая характеристика учебного предмета.

Основная дидактическая идея курса может быть выражена следующей формулой: «через рассмотрение частного к пониманию общего для решения частного». При этом ребенку предлагается постичь суть предмета через естественную связь математики с окружающим миром.

Все это означает, что знакомство с тем или иным математическим понятием осуществляется при рассмотрении конкретной реальной или учебной ситуации, соответствующий анализ которой позволят обратить внимание ученика на суть данного математического понятия. В свою очередь, такая акцентуация дает возможность добиться необходимого уровня обобщений без многочисленного рассмотрения частностей.

Логико – дидактической основной реализации первой части формулы является неполная индукция, которая приведет ученика к самостоятельному «открытию» изучаемого математического факта. Вторая же часть формулы носит дедуктивный характер и направлена на формирование у учащихся умения конкретизировать полученные знания и применять их к решению поставленных задач.

Содержание всего курса можно представить как взаимосвязанное развитие пяти основных содержательных линий: арифметической, геометрической, величинной, алгоритмической и информационной.

Место учебного предмета в учебном плане.

В соответствии с Примерным учебным планом для образовательных учреждений, использующих УМК «Перспективная начальная школа». В 1 классе курс рассчитан на 132 часа.

Ценностные ориентиры содержания учебного предмета.

Ценностные ориентиры содержания курса связаны с целевыми и ценностными установками начального общего образования по математике. В основе учебно-воспитательного процесса лежат такие ценности как:

- восприятие окружающего мира как единого и целостного при познании фактов, процессов, явлений, происходящих в природе и обществе, средствами математических отношений;

- математические представления о числах, величинах, геометрических фигурах являются условием целостного восприятия природы и творений человека;

- владение математическим языком, алгоритмами, элементами математической логики позволяют ученику в его коммуникативной деятельности.

Весь материал - в документе.

Пояснительная записка по МАТЕМАТИКЕ

1 класс (132 ч)

Программа «Математика» Чекина А.Л. и (образовательная программа «Перспективная начальная школа») разработана на основе Федерального государственного образовательного стандарта начального общего образования, основных положений развивающей личностно-ориентированной системы «Перспективная начальная школа», реализующей  межпредметные и внутрипредметные связи, логику учебного процесса, задачи формирования у младшего школьника умения учиться. УМК «Перспективная начальная школа», 2011 г., учебник Чекина А.Л. (Москва, Академкнига/Учебник,2011г.) Курс рассчитан на 132 часа (4 часа в неделю).
Программу обеспечивают:

• Чекин А.Л. Математика. 1 класс: Учебник. В 2 ч. — М.: Академкнига/ Учебник.

• Юдина Е.П. Математика: Тетради для самостоятельной работы №1, №2. — М.; Академкнига/Учебник.

• Чекин А.Л. Математика: Методическое пособие для учителя. В 2 ч. — М.: Академкнига/Учебник.

Цель: ввести ребенка в абстрактный мир математических понятий и их свойств, охватывающих весь материал обязательного минимума начального математического образования и дать первоначальные навыки ориентации в той части реальной действительности, которая описывается (моделируется) с помощью этих понятий, а именно: окружающий мир как множество форм, как множество предметов, отличающихся величиной, которую можно выразить числом как разнообразие классов конечных равночисленных множеств и т.п., а также предложить ребенку соответствующие способы познания окружающей действительности.

Задачи:

- овладение знаниями и умениями, необходимыми для успешного решения учебных и практических задач и продолжения образования;

-развитие личности ребенка, и прежде всего его мышления как основы развития других психических процессов: памяти, внимания, воображения, математической речи и способностей;

-формирование основ общих учебных умений и способов деятельности, связанных с методами познания окружающего мира (наблюдения, измерения, моделирования), приемов мыслительной деятельности (анализ, синтез, сравнение, классификация, обобщение), способов организации учебной деятельности  (планирование, самоконтроль, самооценка и др.).

Основная дидактическая идея курса может быть выражена следующей формулой: через рассмотрение частного к пониманию общего для решения частного. При этом ребенку предлагается постичь суть предмета через естественную связь математики с окружающим миром. Отличительной чертой настоящего курса является значительное увеличение изучения геометрического материала и изучения величин. Изучение же арифметического материала, оставаясь стержнем всего курса, осуществляется с возможным паритетом теоретической и прикладной составляющих, а в вычис­лительном плане особое внимание уделяется способам и технике устных вычислений.

Общая характеристика учебного предмета

Основная дидактическая идея курса может быть выражена следующей формулой: «через рассмотрение частного к пониманию общего для решения частного». При этом ребенку предлагается постичь суть предмета через естественную связь математики с окружающим миром. Все это означает, что знакомство с тем или иным математическим понятием осуществляется при рассмотрении конкретной реальной или учебной ситуации, соответствующий анализ которой позволят обратить внимание ученика на суть данного математического понятия. В свою очередь, такая акцентуация дает возможность добиться необходимого уровня обобщений без многочисленного рассмотрения частностей.

Логико – дидактической основной реализации первой части формулы является неполная индукция, которая приведет ученика к самостоятельному «открытию» изучаемого математического факта. Вторая же часть формулы носит дедуктивный характер и направлена на формирование у учащихся умения конкретизировать полученные знания и применять их к решению поставленных задач.

Содержание всего курса можно представить как взаимосвязанное развитие пяти основных содержательных линий: арифметической, геометрической, величинной, алгоритмической и информационной.

Место учебного предмета в учебном плане

В соответствии с Примерным учебным планом для образовательных учреждений, использующих УМК «Перспективная начальная школа». В 1 классе курс рассчитан на 132 часа.

Ценностные ориентиры содержания учебного предмета

Ценностные ориентиры содержания курса связаны с целевыми и ценностными установками начального общего образования по математике.В основе учебно-воспитательного процесса лежат такие ценности как:

-восприятие окружающего мира как единого и целостного при познании фактов, процессов, явлений, происходящих в природе и обществе, средствами математических отношений;

-математические представления о числах, величинах, геометрических фигурах являются условием целостного восприятия природы и творений человека;

-владение математическим языком, алгоритмами, элементами математической логики позволяют ученику в его коммуникативной деятельности.

Региональный компонент

Формы организации учебного процесса: фронтальные, групповые, индивидуальные, урок-игра, урок-экскурсия и т.д.

Требования к уровню подготовки учащихся по курсу «Математика» к концу первого года обучения

ЛИЧНОСТНЫЕ

У учащихся будут сформированы:

положительное отношение к урокам математики;

могут быть сформированы:

умение признавать собственные ошибки.

МЕТАПРЕДМЕТНЫЕ

Регулятивные

Учащиеся научатся:

отслеживать цель учебной деятельности (с опорой на маршрутные листы) и внеучебной (с опорой на развороты проектной деятельности);

учитывать ориентиры, данные учителем, при освоении нового учебного материала;

проверять результаты вычислений;

адекватно воспринимать указания на ошибки и исправлять найденные ошибки.

Учащиеся получат возможность научиться:

оценивать собственные успехи в вычислительной деятельности;

планировать шаги по устранению пробелов (знание состава чисел).

Познавательные

Учащиеся научатся:

анализировать условие задачи (выделять числовые данные и цель — что известно, что требуется найти);

сопоставлять схемы и условия текстовых задач;

устанавливать закономерности и использовать их при выполнении заданий (продолжать ряд, заполнять пустые клетки в таблице);

осуществлять синтез числового выражения (восстановление деформированных равенств), условия текстовой задачи (восстановление условия по рисунку, схеме, краткой записи);

сравнивать и классифицировать изображенные предметы и геометрические фигуры по заданным критериям;

понимать информацию, представленную в виде текста, схемы, таблицы; дополнять таблицы недостающими данными.

Учащиеся получат возможность научиться:

видеть аналогии и использовать их при освоении приемов вычислений;

конструировать геометрические фигуры из заданных частей; достраивать часть до заданной геометрической фигуры; мысленно делить геометрическую фигуру на части;

сопоставлять информацию, представленную в разных видах;

выбирать задание из предложенных, основываясь на своих интересах.

Коммуникативные

Учащиеся научатся:

сотрудничать с товарищами при выполнении заданий в паре: устанавливать и соблюдать очерёдность действий, сравнивать полученные результаты, выслушивать партнера, корректно сообщать товарищу об ошибках;

задавать вопросы с целью получения нужной информации.

Учащиеся получат возможность научиться:

организовывать взаимопроверку выполненной работы;

высказывать свое мнение при обсуждении задания.

Предметные:

Учащиеся должны знать/понимать:

-количественный и порядковый смысл целого неотрицательного числа;

-смысл действий (операций) сложения и вычитания над целыми неотрицательными числами;

-взаимосвязь между действиями сложения и вычитания;

-свойства сложения: прибавление числа к сумме и суммы к числу;

-свойства вычитания: вычитание числа из суммы и суммы из числа;

-линии: прямая, кривая, ломаная, отрезок, дуга;

-замкнутые и незамкнутые линии;

-внутренняя область, ограниченная замкнутой линией;

-прямой угол;

-многоугольники и их виды;

-измерение длины отрезка;

-все цифры;

-знаки больше (), меньше (

-названия всех однозначных чисел и чисел второго десятка, включая число 20;

-знаки и термины, связанные со сложением и вычитанием (+, —, сумма, значение суммы, слагаемые, разность, значение разности, уменьшаемое, вычитаемое);

-переместительный закон сложения;

-таблицу сложения однозначных чисел и соответствующие случаи вычитания;

-изученные геометрические термины (точка, линия, прямая, кривая, ломаная, отрезок, дуга, замкнутая, незамкнутая, многоугольник, треугольник, четырехугольник, прямой угол, прямоугольник);

-изученные единицы длины (сантиметр, дециметр);

-изученное соотношение между единицами длины (1 дм = 10 см);

-термины, связанные с понятием «задача» (условие, требование, решение, ответ).

Уметь:

-читать и записывать все однозначные числа и числа второго десятка;

-сравнивать изученные числа и записывать результат сравнения с помощью знаков (,

-воспроизводить правила прибавления числа к сумме и суммы к числу;

-воспроизводить и применять переместительное свойство сложения;

-воспроизводить и применять правила сложения и вычитания с нулем;

-распознавать в окружающих предметах или их частях плоские геометрические фигуры (треугольник, четырехугольник, прямоугольник, круг);

-выполнять сложение и вычитание однозначных чисел без перехода через разряд на уровне навыка;

-выполнять сложение однозначных чисел с переходом через разряд и вычитание в пределах таблицы сложения, используя данную таблицу в качестве справочника;

-чертить с помощью линейки прямые, отрезки, ломаные, многоугольники;

-определять прямые углы с помощью угольника;

-определять длину данного отрезка (в сантиметрах) при помощи измерительной линейки;

-строить отрезки заданной длины при помощи измерительной линейки;

-находить значения сумм и разностей отрезков данной длины при помощи измерительной линейки и с помощью вычислений;

-выражать длину отрезка, используя разные единицы длины (например, 1 дм 6 см или 16 см);

-распознавать и формулировать простые задачи;

-составлять задачи по рисунку и делать иллюстрации (схематические) к тексту задачи.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для того, чтобы:

-ориентироваться в окружающем пространстве (вверх, вниз, влево, вправо и др.);

-выделять из множества один или несколько предметов, обладающих или не обладающих указанным свойством;

-пересчитывать предметы и выражать результат числом;

-определять, в каком из множеств больше предметов; сколько предметов в одном множестве, сколько в другом.

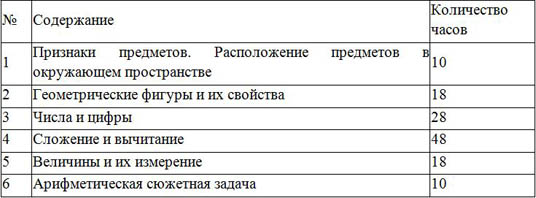
Учебно-тематический план.

Содержание тем учебного курса.

Содержание всего курса можно представить как взаимосвязанное развитие пяти основных содержательных линий: арифметической геометрической, величинной, алгоритмической (обучение решению задач) и алгебраической.

Арифметическая линия прежде всего представлена материалом по изучению чисел.    

Числа  изучаются в такой последовательности:

• натуральные числа от 1 до 10 и число 0 (1-е полугодие 1-го класса),

• целые числа от 0 до 20  (2-е полугодие 1-го класса),

Числа от 1 до 5 и число 0 изучаются на количественной основе.
Числа от 6 до 10 изучаются на аддитивной основе с опорой на число 5. Числа второго десятка и все остальные натуральные числа изучаются на основе принципов нумерации (письменной и устной) десятичной системы счисления.
Особенностью изучения арифметических действий в насто­ящем курсе является строгое следование математической сути этого понятия. Именно поэтому при введении любого арифмети­ческого действия (бинарной алгебраической операции) с самого начала рассматриваются не только компоненты этого действия, но и, в обязательном порядке, его результат.  

Арифметические действия над числами изучаются на следую­щей теоретической основе и такой последовательности:

• Сложение (систематическое изучение начинается с 1 полугодия  1-го класса) определяется на основе объединения непересекающихся множеств и сначала выполняется на множестве чисел от 0 до 5. В дальнейшем изучаются свойства сложе­ния, которые используются при проведении устных и письменных вычислений. Сложение многозначных чисел базируется на знании таблицы сложения однозначных чисел и на поразрядном способе сложения.

• Вычитание (систематическое изучение начинается со 2 полугодия 1-го класса) изначально вводится на основе вычитания подмножества из множества, причем происходит это, когда учащи­еся изучили числа в пределах первого десятка. Далее устанавли­вается связь между сложением и вычитанием, которая опирается на идею обратной операции. На основе этой связи выполняется вычитание с применением таблицы сложения, а потом осущест­вляется переход к рассмотрению случаев вычитания многозначных чисел, где главную роль играет поразрядный принцип вычитания, возможность которого базируется на соответствующих свойствах вычитания.

Геометрическая линия выстраивается следующим образом. 
В 1-м классе изучаются следую­щие геометрические понятия:

• плоская геометрическая фигура (круг, треугольник, прямоугольник),

• прямая и кривая линии, точка, отре­зок, дуга, направленный отрезок (дуга), пересекающиеся и непере­секающиеся линии, ломаная линия, замкнутая и незамкнутая линии,

• внутренняя и внешняя области относительно границы,

• многоуголь­ник, прямой угол, прямоугольник,

• симметричные фигуры.

Линия по изучению величин начинается уже

• в 1 полугодии 1-го класса с изучения величины «длина». Сначала длина рассматривается в доизмерительном аспекте. Сравнение предме­тов по этой величине осуществляется на глаз по рисунку или по представлению, а также способом приложения. Никаких измерений пока не проводится.

• во 2 полугодии 1-го класса учащиеся знакомятся с процессом измерения длины, стандартными единицами длины (сантиметром и дециметром), процедурой сравнения длин на основе их измерения, а также с операциями сложения и вычитания длин.

Линия по обучению решению арифметических сюжетных (текстовых) задач (условно названа «алгоритмической») является центральной для данного курса. Ее особое положение опре­деляется тем, что настоящий курс имеет прикладную направлен­ность, которая выражается в умении применять полученные знания на практике. При этом важно не только научить учащихся решать задачи, но и правильно формулировать их, используя имеющуюся информацию. Под реше­нием задачи понимается запись (описание) алгоритма, дающего возможность выполнить требование задачи. 

Описание алгоритма решения задачи допускается в трех видах:

1. по действиям (по шагам) с пояснениями;

2. в виде числового выражения, но без пояснений;

3. в виде буквенного выраже­ния (в некоторых случаях в виде формулы или в виде уравнения), с использованием стандартной символики.

Алгебраическая линия традиционно представлена такими поня­тиями, как выражение с переменной, уравнение. Изучение этого материала приходится главным образом на 4-й класс, но пропедевтическая работа начинается с 1-го класса - задания,  в которых учащимся предлагается заполнить пропуски соответствующими числами, появление равенств с «окошками», в которые следует записать нужные числа, является пропедевтикой изучения урав­нений.

1. Признаки предметов. Расположение предметов в окружающем пространстве (10 ч)

Отличие предметов по цвету, форме, величине (размеру). Сравнение предметов по величине (размеру): больше, меньше, такой же. Установление идентичности предметов по одному или нескольким признакам. Объединение предметов в группу по общему признаку. Расположение предметов слева, справа, вверху, внизу по отношению к наблюдателю, их комбинация. Расположение предметов над (под) чем-то, левее (правее) чего-то, между одним и другим. Спереди (сзади) по направлению движения. Направление движения налево (направо), вверх (вниз). Расположение предметов по порядку: установление первого и последнего, следующего и предшествующего (если они существуют).

2. Геометрические фигуры и их свойства (18 ч)

Первичные представления об отличии плоских и искривленных поверхностей. Знакомство с плоскими геометрическими фигурами: кругом, треугольником, прямоугольником. Распознавание формы данных геометрических фигур в реальных предметах. Прямые и кривые линии. Точка. Отрезок. Дуга. Изображение направленных отрезков (дуг) с помощью стрелок. Пересекающиеся и непересекающиеся

линии. Точка пересечения. Ломаная линия. Замкнутые и незамкнутые линии. Замкнутая линия как граница области. Внутренняя и внешняя области по отношению к границе. Замкнутая ломаная линия. Многоугольник. Четырехугольник. Пересечение прямых линий под прямым углом. Прямоугольник. Симметричные фигуры.

3. Числа и цифры (28 ч)

Первичные количественные представления: один и несколько, один и ни одного. Число 1 как количественный признак единственности (единичности), т. е. наличие в единственном числе. Цифра 1.

Первый. Число 0 как количественный признак пустого множества. Цифра 0. Пара предметов. Составление пар. Число 2 как количественная характеристика пары. Цифра 2. Второй. Сравнение групп

предметов по количеству с помощью составления пар: больше, меньше, столько же. Сравнение чисел: знаки ,

4. Сложение и вычитание (48 ч)

Сложение чисел. Знак «плюс» (+). Слагаемые, сумма и ее значение. Прибавление числа 1 как переход к непосредственно следующему числу. Прибавление числа 2 как двукратное последовательное прибавление числа 1. Аддитивный состав чисел 3, 4 и 5. Прибавление чисел 3, 4 и 5 как последовательное прибавление чисел их аддитивного состава. Вычитание чисел. Знак «минус» (–). Уменьшаемое, вычитаемое, разность и ее значение. Вычитание числа 1 как переход к непосредственно предшествующему числу. Вычитание по 1 как многократное повторение вычитания числа 1. Переместительное свойство сложения. Взаимосвязь сложения и вычитания. Таблица сложения однозначных чисел (кроме 0). Табличные случаи вычитания. Случаи сложения и вычитания с 0. Группировка слагаемых. Скобки. Прибавление числа к сумме как один из случаев группировки слагаемых. Поразрядное сложение единиц. Прибавление суммы к числу. Способ сложения по частям на основе удобных слагаемых. Вычитание разрядного слагаемого. Вычитание числа из суммы. Поразрядное вычитание единиц без заимствования десятка. Увеличение (уменьшение) числа на некоторое число. Разностное сравнение чисел. Вычитание суммы из числа. Способ вычитания по частям на основе удобных слагаемых.

5. Величины и их измерение (18 ч)

Сравнение предметов по некоторой величине без ее измерения: выше-ниже, шире-уже, длиннее-короче, старше-моложе, тяжелее-легче. Отношение «дороже-дешевле» как обобщение сравнений предметов по разным величинам. Первичные представления о длине пути и расстоянии. Их сравнение на основе понятий «дальше-ближе» и «длиннее-короче».

Длина отрезка. Измерение длины. Сантиметр как единица длины. Дециметр как более крупная единица длины. Сравнение длин на основе их измерения. Сложение и вычитание длин.

Первичные временные представления: части суток, времена года, раньше-позже, продолжительность (длиннее-короче по времени). Понятие о суточной и годовой цикличности: аналогия с движением по кругу.

6. Арифметическая сюжетная задача (10 ч)

Знакомство с формулировкой арифметической сюжетной задачи: условие и требование. Распознавание и составление сюжетных арифметических задач. Нахождение и запись решения задачи в виде числового выражения. Вычисление и запись ответа задачи в виде значения выражения с соответствующим наименованием.

Средством контроля на уроках является самостоятельная работа учеников на основе, которой учитель делает выводы об их достижениях. Отметки в первом классе не ставятся. В конце года проводится комплексная контрольная работа.

Учебно-методические средства обучения:

Чекин А.Л. Математика. 1 класс: Учебник-тетрадь. В 2 ч. — М.: Академкнига/Учебник, 2009.

Юдина Е.П. Математика: Тетрадь для самостоятельной работы №1, №2,— М.: Академкнига/Учебник, 2009.

Чекин А.Л. Математика: Методическое пособие для учителя.. — М.: Академкнига/Учебник,— 2009.

Муниципальное казённое общеобразовательное учреждение

«Средняя общеобразовательная школа №11 пос. Нового»

РАБОЧАЯ ПРОГРАММА

по учебному курсу «Математика»

Пашкиной Юлии Валерьевны

учителя начальных классов

1 класс

Базовый уровень

2014-2015 учебный год