ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Настоящая программа по математике для 9 класса составлена на основе:
Федеральный Закон Российской Федерации от 29 декабря 2012 года № 273 «Об образовании в Российской Федерации» (принят Государственной Думой 21 декабря 2012 года Одобрен Советом Федерации 26 декабря 2012 года, в ред. Федеральных законов от 07.05.2013 N 99-ФЗ, от 23.07.2013 N 203-ФЗ);
Приказ Министерства образования Российской Федерации от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования»;
Приказ Министерства образования Российской Федерации от 09.03.2004 №1312 «Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования»;
Приказ Министерства образования Российской Федерации от 20.08.2008 № 241 «О внесении изменений в федеральный базисный учебный план и примерные учебные планы для образовательных учреждений РФ, реализующих программы общего образования»;
Приказы Министерства образования Российской Федерации от 30.08.2010 № 889, от 03.06.2011 № 1994,от 01.02.2012 № 74 «О внесении изменений в федеральный базисный учебный план и примерные учебные планы для образовательных учреждений РФ, реализующих программы общего образования, утвержденные приказом Минобразования РФ от 9 марта 2004 г. № 1312»;
Приказом МО РФ от 19.10.2009 № 427 «О внесении изменений в федеральный компонент государственных стандартов начального общего образования, основного общего образования, среднего (полного) общего образования» от 05.03. 2004 № 1089;
Гигиенические требования к условиям обучения в общеобразовательных учреждениях. Санитарно-эпидемиологические правила СанПиН 2.4.2.2821-10 от 29.12.2010г.
приказ Министерства образования Сахалинской области от 19.07.2011 № 862-ОД «Об утверждении Регионального базисного учебного плана для общеобразовательных учреждений Сахалинской области»;
Приказ «Об утверждении Перечня учебников для обеспечения образовательного процесса в МБОУ СОШ № 26 на 2014-2015 учебный год» от 05.05.2014 № 213/1;
Приказ об утверждении Годового календарного учебного графика МБОУ СОШ № 26 от 18.06.2014г № 348;
Приказ об утверждении Учебного плана МБОУ СОШ № 26 от 22.04.2014 №187.
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования отводится не менее 875 ч из расчета 5 ч в неделю с V по IX класс. Математика изучается в IX классе 5 ч в неделю, всего 175 ч. Согласно Учебному плану МБОУ СОШ № 26 города Южно-Сахалинска, утвержденного приказом директора от 22.04.14№ 187, из школьного компонента на изучение математики в IX классе добавлен 1 час в неделю (35 часов в год), который распределен по темам и направлен на увеличение количества часов при изучении курса математики IX класса. Исходя из этого, количество учебных часов в году, отведенных на изучение курса математики IX класса составляет 206 часов (6 часов в неделю):
I четверть (9 недель) - 54 часа; II четверть (7 недель) – 42 часа;
III четверть (9 недель и 4 дня) – 58 часов; IV четверть (8 недель и 4 дня) – 52 часа.
Основные функции:
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Общая характеристика учебного предмета
Математическое образование в основной школе складывается из следующих содержательных компонентов: арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия – один из важнейших компонентов математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Общеучебные умения, навыки и способы деятельности.
В ходе преподавания математики в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Основная форма организации образовательного процесса – классно-урочная система.
Предусматривается применение следующих технологий обучения:
традиционная классно-урочная
игровые технологии
технология развивающего обучения
лекционно-семинарская система обучения
технологии уровневой дифференциации
здоровьесберегающие технологии
ИКТ
Виды и формы контроля: самостоятельная работа, контрольная работа, тестирование, работа по карточке, устный ответ.
Дифференцированные самостоятельные работы, содержащие задания обязательного и повышенного уровня, рассчитанные на 5-20 минут, оцениваемые отметкой «2» - не сделан обязательный уровень, «3» - правильно выполнен обязательный уровень, «4» - если допущена одна ошибка или несколько неточностей , «5» - правильно выполнены все задания или допущена неточность, не приведшая к неправильному решению.
Дифференцированные контрольные работы, содержащие задания обязательного и повышенного уровня, время выполнения – 45 минут, оцениваемые отметкой «2» - не сделан обязательный уровень, «3» - правильно выполнен обязательный уровень, «4» - если допущена одна ошибка или несколько неточностей, «5» - правильно выполнены все задания или допущена неточность, не приведшая к неправильному решению.
Тестирование
«5» - 90-100%; «4» - 71-90%; «3» - 51-70%; «2» - 50% и менее.
Работа по карточкам (в том числе устно)
«5» - правильные ответы на все вопросы.
«4» - на основной вопрос ответ верный, но на дополнительные не ответил или допустил ошибку.
«3» - затруднился, дал не полный ответ, отвечал на дополнительные вопросы.
«2» - не знает ответ и на дополнительные вопросы отвечает с трудом.
1. Устный ответ.
Оценка “5” ставится, если ученик:
Показывает глубокое и полное знание и понимание всего объёма программного материала; полное понимание сущности рассматриваемых понятий, явлений и закономерностей, теорий, взаимосвязей;
Умеет составить полный и правильный ответ на основе изученного материала; выделять главные положения, самостоятельно подтверждать ответ конкретными примерами, фактами; самостоятельно и аргументировано делать анализ, обобщения, выводы. Устанавливать межпредметные (на основе ранее приобретенных знаний) и внутрипредметные связи, творчески применять полученные знания в незнакомой ситуации. Последовательно, чётко, связно, обоснованно и безошибочно излагать учебный материал; давать ответ в логической последовательности с использованием принятой терминологии; делать собственные выводы; формулировать точное определение и истолкование основных понятий, законов, теорий; при ответе не повторять дословно текст учебника; излагать материал литературным языком; правильно и обстоятельно отвечать на дополнительные вопросы учителя. Самостоятельно и рационально использовать наглядные пособия, справочные материалы, учебник, дополнительную литературу, первоисточники; применять систему условных обозначений при ведении записей, сопровождающих ответ; использование для доказательства выводов из наблюдений и опытов;
Самостоятельно, уверенно и безошибочно применяет полученные знания в решении проблем на творческом уровне; допускает не более одного недочёта, который легко исправляет по требованию учителя; имеет необходимые навыки работы с приборами, чертежами, схемами и графиками, сопутствующими ответу; записи, сопровождающие ответ, соответствуют требованиям.
Оценка “4” ставится, если ученик:
Показывает знания всего изученного программного материала. Даёт полный и правильный ответ на основе изученных теорий; незначительные ошибки и недочёты при воспроизведении изученного материала, определения понятий дал неполные, небольшие неточности при использовании научных терминов или в выводах и обобщениях из наблюдений и опытов; материал излагает в определенной логической последовательности, при этом допускает одну негрубую ошибку или не более двух недочетов и может их исправить самостоятельно при требовании или при небольшой помощи преподавателя; в основном усвоил учебный материал; подтверждает ответ конкретными примерами; правильно отвечает на дополнительные вопросы учителя.
Умеет самостоятельно выделять главные положения в изученном материале; на основании фактов и примеров обобщать, делать выводы, устанавливать внутрипредметные связи. Применять полученные знания на практике в видоизменённой ситуации, соблюдать основные правила культуры устной речи и сопровождающей письменной, использовать научные термины;
Не обладает достаточным навыком работы со справочной литературой, учебником, первоисточниками (правильно ориентируется, но работает медленно). Допускает негрубые нарушения правил оформления письменных работ.
Оценка “3” ставится, если ученик:
усвоил основное содержание учебного материала, имеет пробелы в усвоении материала, не препятствующие дальнейшему усвоению программного материала;
материал излагает несистематизированно, фрагментарно, не всегда последовательно;
показывает недостаточную сформированность отдельных знаний и умений; выводы и обобщения аргументирует слабо, допускает в них ошибки.
допустил ошибки и неточности в использовании научной терминологии, определения понятий дал недостаточно четкие;
не использовал в качестве доказательства выводы и обобщения из наблюдений, фактов, опытов или допустил ошибки при их изложении;
испытывает затруднения в применении знаний, необходимых для решения задач различных типов, при объяснении конкретных явлений на основе теорий и законов, или в подтверждении конкретных примеров практического применения теорий;
отвечает неполно на вопросы учителя (упуская и основное), или воспроизводит содержание текста учебника, но недостаточно понимает отдельные положения, имеющие важное значение в этом тексте;
обнаруживает недостаточное понимание отдельных положений при воспроизведении текста учебника (записей, первоисточников) или отвечает неполно на вопросы учителя, допуская одну-две грубые ошибки.
Оценка “2” ставится, если ученик:
не усвоил и не раскрыл основное содержание материала;
не делает выводов и обобщений.
не знает и не понимает значительную или основную часть программного материала в пределах поставленных вопросов;
или имеет слабо сформированные и неполные знания и не умеет применять их к решению конкретных вопросов и задач по образцу;
или при ответе (на один вопрос) допускает более двух грубых ошибок, которые не может исправить даже при помощи учителя.
Примечание.
По окончанию устного ответа учащегося педагогом даётся краткий анализ ответа, объявляется мотивированная оценка. Возможно привлечение других учащихся для анализа ответа, самоанализ, предложение оценки.
В основу содержания и структурирования данной программы, выбора приемов, методов и форм обучения положено формирование универсальных учебных действий, которые создают возможность самостоятельного успешного усвоения обучающимися новых знаний, умений и компетентностей, включая организацию усвоения, т.е. умения учиться. В процессе обучения математики осуществляется развитие личностных, регулятивных, познавательных и коммуникативных действий. Учащиеся продолжают овладение разнообразными способами познавательной, информационно-коммуникативной, рефлексивной деятельности, приобретают и совершенствуют опыт.
Обучение построено на последовательном изучении разделов курса математики. Единый курс построен в форме последовательности тематических блоков с чередованием материала по алгебре, геометрии, комбинаторики, статистике и вероятностей.
Указание ведущих форм, методов и технологий обучения.
Организация учебно-воспитательного процесса требует для успешной реализации учебной программы использовать разнообразные формы организации познавательной деятельности и методы обучения: групповая работа, индивидуальная работа, работа в парах сменного состава. Необходимо использовать в работе индивидуальные задания, различные формы самостоятельной работы, работу с учебником, различного вида творческие работы, консультирование для создания благоприятных условий для развития каждого школьника. Необходимо широко применять ИКТ, различные электронные ресурсы, различные видеопросмотры и видеотренинги. Они включают в себя получение отзыва о просмотре, обсуждение и анализ видеоматериалов. Шире использовать методы обучения с помощью компьютерных программ, которые должны стать хорошим дополнением и наглядным средством для школьников, но они не могут заменить уроков. Их целесообразно использовать при подготовке к занятиям, а также для закрепления и повторения материала. Проводить семинары обучающего характера с целью формирования учебных компетенций, использовать зачетную систему работы для формирования самостоятельности и ответственности учащихся за результаты своего труда. Выбор методов обучения зависит от целей. При передаче учащимся знания больше всего для этого подойдут лекция, групповая дискуссия, уроки, построенные в форме вопросов и ответов. При обучении каким-либо навыкам, это можно сделать с помощью тренингов, практикумов, деловых и ролевых игр, разбора практических ситуаций. Это позволит создать условия для дальнейшей социальной адаптации детей и для максимально возможного развития всех учащихся для выполнения ими различного рода деятельности. Среди форм и методов внеурочной работы широкими возможностями выявления и развития одаренных учащихся обладают различные элективные курсы, конкурсы, привлечение учащихся к участию в различных олимпиадах и конкурсов вне школы и система внеурочной исследовательской работы учащихся.
Указание используемых форм, способов и средств проверки и оценки результатов обучения.
При реализации программы для проверки и оценки результативности обучения мы используем в работе: различные виды самостоятельных работ, индивидуальные, дифференцированные; репродуктивные, творческие; задания в тестовой форме, контрольные работы, творческие работы, зачеты, практические работы, для более объективного и быстрого контроля знаний используем тестовые задания.
Система уроков при обучении условна, но выделяются следующие виды:
Урок-лекция – предполагается совместная деятельность учителя и учеников для решения общей проблемной познавательной задачи.
Урок практикум – учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть разными: письменные исследования, решение практических задач, изучение свойств функций, свойств геометрических фигур, практическое применение различных методов решения задач.
Урок-исследование – на уроке учащиеся решают проблемные задачи исследовательского характера.
Комбинированный урок – предполагает выполнение заданий и работ различного вида.
Урок решения задач – вырабатываются у учащихся умения и навыки решения задач обязательной и возможной подготовки.
Урок-тест – проводится с целью выявления пробелов знаний учащихся, контроля знаний и тренировки навыков тестовой работы.
Урок-самостоятельная работа – проводятся различные самостоятельные работы дифференцированного характера, уровень обязательной подготовки (3) и уровень возможной подготовки (4 и 5).
Урок-контрольная работа – дифференцированного характера.
Обучение математике в 9 классе направлено на достижение следующих целей:
Овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования.
Интеллектуальное развитие, продолжение формирований качеств личности, свойственных математической деятельности: ясности и точности мышления, критичности мышления, интуиции как свернутого сознания, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей.
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание культуры личности, внимания как свернутого контроля, отношения к математике как к части общечеловеческой культуры.
Основные развивающие и воспитательные цели
Развитие:
- Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
- Математической речи;
- Сенсорной сферы; двигательной моторики; внимания; памяти;
- Навыков само и взаимопроверки.
- Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
- Культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
- Волевых качеств; коммуникабельности; ответственности.
Цели и задачи, решаемые при реализации рабочей программы:
- расширить сведения о свойствах функций, ознакомить учащихся со свойствами и графиком квадратичной функции, выработать умение строить график квадратичной функции и применять графические представления для решения неравенств второй степени с одной переменной;
- выработать умение решать простейшие системы, содержащие уравнения второй степени с двумя переменными, и решать текстовые задачи с помощью составления таких систем;
дать понятие об арифметической и геометрической прогрессиях как числовых последовательностях особого вида;
- научить учащихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов и метода координат при решении геометрических задач;
- развить умение применять тригонометрический аппарат при решении геометрических задач;
- расширить знание учащихся о многоугольниках; рассмотреть понятия длины окружности и площади круга и формулы их вычисления;
- познакомить учащихся с понятием движения и его свойствами, с основными видами движений;
- дать представление о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
- формировать ИКТ компетентность через уроки с элементами ИКТ;
формировать навык работы с тестовыми заданиями;
- подготовить учащихся к итоговой аттестации в новой форме.
Место предмета в федеральном базисном учебном плане
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и показывает распределение учебных часов по разделам курса. Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики в 9 классе отводится 5 часов в неделю, из них на изучение алгебры – 3 часа в неделю, и на изучение геометрии 2 часа в неделю. За счет регионального компонента на изучение математики в школе выделяется 1 дополнительный час, который отводится на изучение алгебры (35 часов) Дополнительные часы используются для расширения знаний и умений по отдельным темам всех разделов курса.
Учебно-методический комплекты:
I. Мордкович А.Г. Алгебра. 9 класс. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений/А.Г.Мордкович, П.В. Семенов - 11-е изд., стер. – М.: Мнемозина, 2009.
Алгебра. 9 класс. В 2 ч. Ч.2. Задачник для учащихся общеобразовательных учреждений/А.Г.Мордкович, Л.А.Александрова, Т.Н. Мишустина и др./; под ред. А.Г.Мордковича. – 10-е изд., перераб. и доп. – М.: Мнемозина, 2008.
II. 7-9 класс: Геометрия, Атанасян Л.С. и др. Данный УМК хорошо зарекомендовал себя, используется в работе уже несколько лет. Эти учебники обеспечивают преемственность курсов математики 5-6 классов. Позволяют проводить разноуровневое обучение и качественную подготовку школьников, содержит весь необходимый для изучения материал, изложенный в Федеральном компоненте государственных образовательных стандартов основного общего и среднего общего образования, как на базовом, так и на профильном уровне.
Отличительные особенности рабочей программы по сравнению с примерной:
|
Раздел | Количество часов в примерной программе | Количество часов в рабочей программе |
| 1. Повторение курса 7 класса. | 0 | 5 |
| 2. Алгебраические дроби. | 21 | 26 |
| 3. Функция y= √x. Свойства квадратного корня. | 18 | 25 |
| 4. Квадратичная функция. Функция y= k/x. | 18 | 24 |
| 5. Квадратные уравнения. | 21 | 24 |
| 6. Неравенства. | 15 | 18 |
| 7. Обобщающее повторение. | 9 | 13 |
Внесение данных изменений позволит охватить весь изучаемый материал по программе, повысить уровень обученности учащихся по предмету, а также более эффективно осуществить индивидуальный подход к обучающимся.
Срок реализации рабочей учебной программы – один учебный год.
Уровень обучения: базовый.
Содержание учебного материала
УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН
Модуль АЛГЕБРА
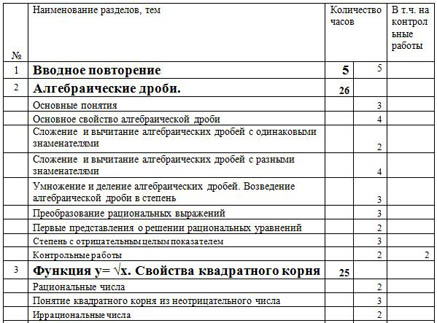
| № | Наименование разделов, тем | Количество часов | В т.ч. на контрольные работы |
| 1 | Вводное повторение | 5 | 5 | |
| 2 | Алгебраические дроби. | 26 | | |
| | Основные понятия | | 3 | |
| | Основное свойство алгебраической дроби | | 4 | |
| | Сложение и вычитание алгебраических дробей с одинаковыми знаменателями | | 2 | |
| | Сложение и вычитание алгебраических дробей с разными знаменателями | | 4 | |
| | Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень | | 3 | |
| | Преобразование рациональных выражений | | 3 | |
| | Первые представления о решении рациональных уравнений | | 2 | |
| | Степень с отрицательным целым показателем | | 3 | |
| | Контрольные работы | | 2 | 2 |
| 3 | Функция y= √x. Свойства квадратного корня | 25 | | |
| | Рациональные числа | | 2 | |
| | Понятие квадратного корня из неотрицательного числа | | 3 | |
| | Иррациональные числа | | 2 | |
| | Множество действительных чисел | | 2 | |
| | Функция y= √x , ее свойства и график | | 3 | |
| | Свойства квадратных корней | | 3 | |
| | Преобразование выражений, содержащих операцию извлечения квадратного корня | | 5 | |
| | Модуль действительного числа | | 4 | |
| | Контрольные работы | | 1 | 1 |
| 4 | Квадратичная функция. Функция y= k/x | 24 | | |
| | Функция у=kx2,ее свойства и график | | 4 | |
| | Функция у=k/x,ее свойства и график | | 4 | |
| | Параллельный перенос графика функции (вправо, влево) | | 3 | |
| | Параллельный перенос графика функции (вверх, вниз) | | 2 | |
| | Параллельный перенос графика функции | | 3 | |
| | Функция у = ах2 + bx + c, ее свойства и график | | 4 | |
| | Графическое решение квадратных уравнений | | 2 | |
| | Контрольные работы | | 2 | 2 |
| 5 | Квадратные уравнения | 24 | | |
| | Основные понятия | | 2 | |
| | Формулы корней квадратного уравнения | | 3 | |
| | Рациональные уравнения | | 4 | |
| | Рациональные уравнения, как математические модели реальных ситуаций | | 4 | |
| | Еще одна формула корней квадратного уравнения | | 2 | |
| | Теорема Виета | | 3 | |
| | Иррациональные уравнения | | 4 | |
| | Контрольные работы | | 2 | 2 |
| 6 | Неравенства | 18 | | |
| | Свойства числовых неравенств | | 4 | |
| | Исследование функции на монотонность | | 3 | |
| | Решение линейных неравенств | | 3 | |
| | Решение квадратных неравенств | | 4 | |
| | Приближенные значения действительных чисел | | 2 | |
| | Стандартный вид числа | | 1 | |
| | Контрольные работы | | 1 | 1 |
| 8 | Обобщающее повторение | 13 | 13 | |
| | ИТОГО | 135 | 135 | 9 |
Модуль ГЕОМЕТРИЯ
| 1 | Вводное повторение | 2 | 2 | |
| 2 | Четырехугольники. | 14 | | |
| | Многоугольники | | 2 | |
| | Параллелограмм и его свойства. | | 2 | |
| | Признаки параллелограмма. | | 2 | |
| | Трапеция. | | 2 | |
| | Прямоугольник. | | 1 | |
| | Ромб и квадрат. | | 2 | |
| | Осевая и центральная симметрия. | | 1 | |
| | Решение задач. | | 1 | |
| | Контрольная работа. | | 1 | 1 |
| 3 | Площадь. | 14 | | |
| | Площадь многоугольника. | | 2 | |
| | Площадь параллелограмма. | | 1 | |
| | Площадь треугольника. | | 2 | |
| | Площадь трапеции. | | 1 | |
| | Решение задач. | | 2 | |
| | Теорема Пифагора. | | 3 | |
| | Решение задач | | 2 | |
| | Контрольная работа. | | 1 | 1 |
| 4 | Подобные треугольники. | 19 | | |
| | Определение подобных треугольников. | | 2 | |
| | Первый признак подобия треугольников. | | 2 | |
| | Второй признак подобия треугольников. | | 1 | |
| | Третий признак подобия треугольников. | | 1 | |
| | Решение задач. | | 1 | |
| | Контрольная работа. | | 1 | 1 |
| | Средняя линия треугольника. | | 2 | |
| | Пропорциональные отрезки в прямоугольном треугольнике. | | 2 | |
| | Решение задач | | 2 | |
| | Соотношение между сторонами и углами прямоугольного треугольника. | | 4 | |
| | Контрольная работа. | | 1 | 1 |
| 5 | Окружность. | 17 | | |
| | Касательная и окружность. | | 3 | |
| | Градусная мера дуги. | | 1 | |
| | Теорема о вписанном угле. | | 2 | |
| | Решение задач | | 1 | |
| | Четыре замечательные точки. | | 3 | |
| | Вписанная окружность. | | 2 | |
| | Описанная окружность. | | 2 | |
| | Решение задач. | | 2 | |
| | Контрольная работа. | | 1 | 1 |
| 6 | Обобщающее повторение | 4 | 4 | |
| | ИТОГО | 70 | 70 | 5 |
Контрольных работ – 14: по геометрии – 5, по алгебре – 9.
Требования к уровню подготовки учащихся:
Требования к результатам обучения направлены на реализацию деятельностного и личностно ориентированного подходов; освоение учащимися интеллектуальной и практической деятельности; овладение знаниями и умениями, востребованными в повседневной жизни, позволяющими ориентироваться в окружающем мире, значимыми для сохранения окружающей среды и собственного здоровья.
Рубрика «Знать/понимать» включает требования к учебному материалу, которые усваиваются и воспроизводятся учащимися.
Рубрика «Уметь» включает требования, основанные на более сложных видах деятельности, в том числе творческой: объяснять, изучать, распознавать и описывать, выявлять, сравнивать, определять, анализировать и оценивать, проводить самостоятельный поиск необходимой информации и т.д.
В результате изучения курса алгебры 9 класса обучающиеся должны:
Знать/понимать
Существо понятия математического доказательства, приводить примеры доказательств.
Существо понятия алгоритма, приводить примеры алгоритмов.
Как используются математические формулы, уравнения и неравенства, примеры их применения для решения математических и практических задач.
Как математически определенные функции могут описывать реальные зависимости, приводить примеры таких описаний
Как потребности практики привели математическую науку к необходимости расширения понятия числа.
Вероятностный характер многих закономерностей окружающего мира, примеры статистических закономерностей и выводов.
Каким образом геометрия возникла из практических задач землемерия, примеры геометрических объектов и утверждений о них, важных для практики.
Смысл формализации, позволяющий решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при формализации.
Арифметика
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе с использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычислений с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
Уметь
составлять формулу по условию задачи; осуществлять числовые подстановки и выполнять соответствующие вычисления в формулах, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через другую;
применять свойства арифметических корней для вычисления значений и преобразования числовых выражений, содержащих корни;
решать линейные, квадратные и рациональные уравнения, сводящиеся к ним, системы двух уравнений, линейные и несложные нелинейные;
решать линейные и квадратные неравенства и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа на координатной прямой и точки с заданной координатой на координатной плоскости; изображать множество решений неравенства на координатной прямой;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значение функции по ее аргументу, значение аргумента по значению функции;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; находить нужные формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами
Геометрия
уметь
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задачи; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин, в том числе тригонометрических функций; находить стороны, углы и площади треугольников, правильных многоугольников, некоторых четырехугольников, длины ломаных и дуг окружности; находить площади основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами.
Элементы логики, комбинаторики, статистики и теории вероятностей
Уметь
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждения;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятность случайного события в простейших случаях.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве в диалоге;
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности;
решения учебных и практических задач, требующих системного перебора вариантов;
сравнения шансов наступления случайных событий, для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
Методы и приемы, используемые при обучении математике:
-Принципы технологии уровневой дифференциации;
-Блоки домашних заданий по алгебре и геометрии;
-Применение интерактивной доски на различных этапах учебной деятельности для активизации учебного процесса.
Литература и методическое обеспечение
а) для учителя:
1.Стандарт основного общего образования по математике. Официальный документ.
2.Примерные программы для общеобразовательных учреждений по алгебре 7-9 классы к учебному комплексу для 7-9 классов (составители И.И.Зубарева, А.Г.Мордкович. – М.: Мнемозина, 2009).
3. Авторская программа Атанасян Л.С., Бутузов В.Ф., Кодомцев С.Б. составитель БурмистроваТ.А., М. «Просвещение», 2009
4.А.Г.Мордкович. Алгебра – 8. В 2 ч. Ч.1. Учебник. Мнемозина, 2010 г.
5. А.Г.Мордкович. Алгебра – 8. В 2 ч. Ч.2. Задачник. Мнемозина, 2010 г.
6.Л.А.Александрова. Алгебра – 8. Контрольные работы./Под ред. А.Г.Мордковича. Мнемозина, 2009 г.
7. Л.А.Александрова. Алгебра – 8. Самостоятельные работы./Под ред. А.Г.Мордковича. Мнемозина, 2009
8.Л.С.Атанасян. Геометрия 7-9. Учебник для общеобразовательных учреждений. Просвещение, 2009 г.
9. А.Г.Мордкович. Алгебра, 7-9. Тесты. Мнемозина.2009г.
10. А.Г.Мордкович. Алгебра, 7-9. Методическое пособие для учителя. Мнемозина.2009г.
11. Б.Г.Зив. Дидактические материалы по геометрии, 8класс. Просвещение, 2009г.
12. Л.С.Атанасян. Изучение геометрии в 7-9 классах. Методические рекомендации к учебнику. Просвещение, 2009г.
б) для учащихся:
1.А.Г.Мордкович. Алгебра – 8. В 2 ч. Ч.1. Учебник. Мнемозина, 2010 г.
2. А.Г.Мордкович. Алгебра – 8. В 2 ч. Ч.2. Задачник. Мнемозина, 2010 г.
3. Л.С.Атанасян. Геометрия 7-9. Учебник для общеобразовательных учреждений. Просвещение, 2009 г.
4.Б.Г.Зив. Геометрия: дидактические материалы для 8 класса. Просвещение, 2009г
в) Технические средства обучения
Компьютер, медиапроектор, интерактивная доска
г) Интернет-ресурс
1. www. edu - "Российское образование" Федеральный портал.
2. www. school.edu - "Российский общеобразовательный портал".
3. www.school-collection.edu.ru/ Единая коллекция цифровых образовательных ресурсов
4. www.mathvaz.ru - docье школьного учителя математики
Документация, рабочие материалы для учителя математики
5. www.it-n.ru"Сеть творческих учителей"
6. www .festival.1september.ru Фестиваль педагогических идей "Открытый урок"
7. Учительский портал: http://www.uchportal.ru
8. Современный учительский портал: http://easyen.ru
9. Портал Прошколу: http://www.proshkolu.ru
10. Образовательный портал «Мой университет»: http://www.moi-universitet.ru
11. Портал ИнфоУрок: http://infourok.ru
12. Сервис проверки знаний учащихся http://www.diagtest.ru/
13. ЕГЭ по математике http://uztest.ru/ Общие сведения об экзамене, структура заданий. Онлайн-тестирование с проверкой правильности решения задач, тренажер, дистанционный курс. Варианты заданий прошлых лет. Конспекты. Материалы для учителя.
38

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (9-й класс) (74.64 КB)
Рабочая программа по математике (9-й класс) (74.64 КB)
 0
0 947
947 4
4 Нравится
0
Нравится
0








