Муниципальное автономное общеобразовательное учреждение
«Средняя общеобразовательная школа № 38»
«Утверждено»
Педагогическим советом
протокол от ________2013г. №____
Введено приказом от_____2013г. №___
Директор школы
_____________ ___________________
Подпись Ф.И.О.
Рабочая программа
по предмету математика
для 5 Г класса (6 часов в неделю, 210 часов в год)
Составитель: Шаруда Жанна Николаевна
(учитель математики, второй квалификационной категории)
«Согласовано»
Заместитель директора___________ ________________________ от_________2012г.
Подпись Ф.И.О.
«Рассмотрено»
На заседании МО, протокол от______2013г. №____
Руководитель МО ___________ _________________________ от_________2012г.
Подпись Ф.И.О.
г. Набережные Челны
2013г
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа учебного курса математики для 5 Г класса составлена на основании следующих нормативно-правовых документов:
Федерального компонента государственного стандарта основного общего образования по математике, утвержденного приказом Минобразования РФ от 5.03.2004 г. № 1089.
Примерных программ основного общего образования по математике. / сборника “Программы общеобразовательных учреждений. Математика 5- 6 класс”, “ Т. А. Бурмистрова, Москва, Просвещение, 2010г/
Федерального перечня учебников, рекомендованных (допущенных) МО и НРФ к использованию в образовательном процессе в общеобразовательных учреждениях, реализующих программы общего образования
Учебного плана МАОУ «СОШ № 38» города Набережные Челны Республики Татарстан на 2013-2014 учебный год, утверждённого приказом от 28.08.13 № 312
Программа рассчитана на 210 часов в год (6 часов в неделю), из них:
на итоговое повторение в 5 классе в конце года 20 часов, остальные часы распределены по всем темам;
на плановые контрольные работы отведено 8 часов.
Согласно базисному учебному плану на изучение математики в 5 классе отводится 5 часов в неделю и 1 час в неделю за счёт школьного компонента.
Дополнительные 35 часов направлены на изучение новых тем и расширенное и углубленное изучение тем программы (приложение 1).
«Элементы комбинаторики, статистики и теории вероятностей» изучаются в количестве 14 часов.
Преобладающей формой текущего контроля выступает письменный (самостоятельные, контрольные и тестовые работы), устный опрос.
Обучение ведется по учебнику С. М. Никольского «Математика 5 класс», Москва, Просвещение, 2010г.
Изучение математики в 5 классе направлено на реализацию целей и задач, сформулированных в Государственном стандарте общего образования по математике.
Целями изучения курса математики в 5 классе являются систематическое развитие понятия числа, выработка умений выполнять устно и письменно арифметические действия над натуральными и дробными числами, умение переводить практические задачи на язык математики, подготовка учащихся к изучению курса алгебры и геометрии.
Курс строится на индуктивной основе с привлечением элементов дедуктивных рассуждений. Теоретический материал излагается на интуитивном уровне, математические методы и законы формулируются в виде правил.
В ходе изучения курса учащиеся развивают навыки вычислений с обыкновенными дробями, получают начальные представления об использовании букв для записи выражений и свойств арифметических действий, составления уравнений, продолжают знакомиться с геометрическими понятиями, приобретают навыки построения геометрических фигур и измерения геометрических величин.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Общеучебные умения, навыки и способы деятельности.
В ходе преподавания математики в основной школе, работы над формированием у учащихся, перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Приложение 1 . Календарно – тематический план по математике в 5 классе, автор учебника С. М. Никольский
| № |
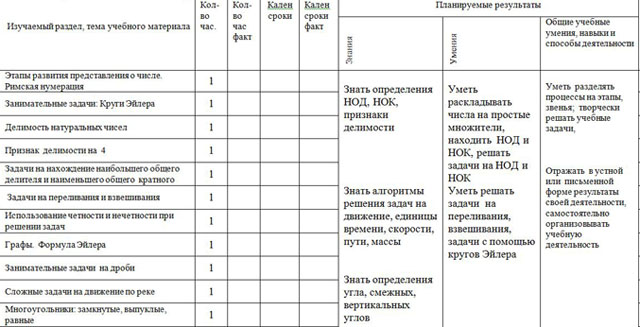
Изучаемый раздел, тема учебного материала | Кол-во час. | Кол-во час факт | Кален сроки | Кален сроки факт | Планируемые результаты | Контрольно – измерительные материалы |
| Знания | Умения | Общие учебные умения, навыки и способы деятельности |
| 1 | Этапы развития представления о числе. Римская нумерация | 1 |
|
|
|
Знать определения НОД, НОК, признаки делимости
Знать алгоритмы решения задач на движение, единицы времени, скорости, пути, массы
Знать определения угла, смежных, вертикальных углов
Знать определение треугольника, виды треугольников: равнобедренные, равносторонние |
Уметь раскладывать числа на простые множители, находить НОД и НОК, решать задачи на НОД и НОК Уметь решать задачи на переливания, взвешивания, задачи с помощью кругов Эйлера
Уметь решать простейшие комбинаторные задачи, вычислять вероятность события
Уметь решать задачи на нахождение чисел по их сумме и разности
|
Уметь разделять процессы на этапы, звенья; творчески решать учебные задачи,
Отражать в устной или письменной форме результаты своей деятельности, самостоятельно организовывать учебную деятельность
Владеть навыками самооценки своей учебной деятельности |
|
| 2 | Занимательные задачи: Круги Эйлера | 1 |
|
|
|
|
| 3 | Делимость натуральных чисел | 1 |
|
|
|
|
| 4 | Признак делимости на 4 | 1 |
|
|
|
|
| 5 | Задачи на нахождение наибольшего общего делителя и наименьшего общего кратного | 1 |
|
|
|
|
| 6 | Задачи на переливания и взвешивания | 1 |
|
|
|
|
| 7 | Использование четности и нечетности при решении задач | 1 |
|
|
|
|
| 8 | Графы. Формула Эйлера | 1 |
|
|
|
|
| 9 | Занимательные задачи на дроби | 1 |
|
|
|
|
| 10 | Сложные задачи на движение по реке | 1 |
|
|
|
|
| 11 | Многоугольники: замкнутые, выпуклые, равные | 1 |
|
|
|
|
| 12 | Ромб | 1 |
|
|
|
|
| 13 | Длина ломаной. Периметр прямоугольника | 1 |
|
|
|
|
| 14 | Занимательные задачи на разрезание отрезков, прямоугольников. | 1 |
|
|
|
|
| 15 | Измерение углов. Смежные и вертикальные углы | 1 |
|
|
|
|
| 16 | Виды треугольников: равнобедренные, равносторонние. | 1 |
|
|
|
| 17 | Координаты середины отрезка | 1 |
|
|
|
| 17 | Наглядные представления о пространственных телах: кубе, параллелепипеде. | 1 |
|
|
|
| 18 | Куб. Развертка куба | 1 |
|
|
|
| 19 | Представление данных в виде таблицы | 1 |
|
|
|
| 20 | Представление данных в виде диаграмм | 1 |
|
|
|
|
| 21 | Вычисления с помощью калькулятора | 1 |
|
|
|
|
| 22 | Решение комбинаторных задач: перебор вариантов | 1 |
|
|
|
|
| 23 | Понятия и примеры случайных событий | 1 |
|
|
|
|
| 24 | Понятия достоверных, невозможных событий | 1 |
|
|
|
| 25 | Понятие вероятности случайного события | 1 |
|
|
|
| 26 | Решение задач на деление с остатком | 1 |
|
|
|
| 27 | Задачи «на части» | 1 |
|
|
|
| 28 | Задачи на сплавы | 1 |
|
|
|
| 29 30 | Задачи на нахождение двух чисел по их сумме и разности | 2 |
|
|
|
|
| 31 | Задачи на движение | 1 |
|
|
|
|
| 32 | Старинные задачи на нахождение части от целого, целого по его части | 1 |
|
|
|
|
| 33 | Задачи на прохождения некоторого пути. | 1 |
|
|
|
| 34 35 | Решение задач | 2 |
|
|
|
|
СОДЕРЖАНИЕ программного учебного курса математики в 5 классе
Глава 1. Натуральные числа и нуль ( 52)
Ряд натуральных чисел. Десятичная система исчисления. Запись числа в виде суммы разрядных слагаемых. Сравнение натуральных чисел. Сравнение единиц измерения. Арифметические действия над натуральными числами. Сложение натуральных чисел. Законы арифметических действий: переместительный, сочетательный. Законы сложения. Вычитание натуральных чисел. Компоненты вычитания в уравнениях.
Решение текстовых задач арифметическим способом, с помощью сложения. Решение текстовых задач, с помощью вычитания.
Умножение натуральных чисел. Переместительный закон умножения. Сочетательный закон умножения Решение задач с помощью числовых выражений. Задачи на нахождение двух чисел по их сумме и разности. Переместительный закон умножения. Распределительный закон. Вынесение общего множителя за скобки. Сложение чисел столбиком Вычитание чисел столбиком. Числовые выражения..
Умножение чисел столбиком. Умножение круглых чисел. Решение задач на умножение чисел. Степень с натуральным показателем.
Запись числа в виде степени. Деление нацело. Свойство частного. Свойства деления. Деление суммы на число. Решение текстовых задач с помощью умножения. Решение текстовых задач с помощью деления. Задачи «на части». Задачи «на части», если известна сумма. Задачи «на части», если известна разность. Деление нацело. Деление с остатком. Решение задач на деление с остатком. Числовые выражения, порядок действий в них, использование скобок. Вычисления с помощью калькулятора. Этапы развития представления о числе. Римская нумерация. Занимательные задачи: Круги Эйлера Задачи на переливания, взвешивания
Глава 2. Измерение величин (38)
Точка. Прямая. Луч. Отрезок. Параллельные и пересекающиеся прямые. Измерение отрезков. Расстояние между точками.
Метрические единицы измерения длины. Запись измерения с недостатком, с избытком. Изображение натуральных чисел точками на координатном луче. Определение координат точек на координатном луче. Геометрические фигуры и некоторые тела. Окружность и круг: центр, радиус, диаметр, дуга, хорда. Сфера и шар Углы. Прямой угол. Острые и тупые углы. Измерение углов. Смежные и вертикальные углы Виды треугольников: равнобедренные, равносторонние. Периметр треугольника. Вычисление сторон треугольника Четырехугольники. Периметр четырехугольника. Ромб. Площадь прямоугольника. Площадь квадрата. Единицы измерения площади Прямоугольный параллелепипед. Куб.
Объём прямоугольного параллелепипеда. Объем куба. Единицы измерения объёма. Занимательные задачи на разрезание отрезков, прямоугольников
Глава 3. Делимость натуральных чисел (25)
Делимость натуральных чисел. Свойства делимости . Единицы измерения массы. Единицы измерения времени, длительность процессов в окружающем мире. Представление данных в виде таблицы. Задачи на движение. Движение по реке. Единицы измерения скорости. Скорость удаления, скорость сближения. Многоугольники: замкнутые, выпуклые, равные. Длинна ломаной. Периметр прямоугольника.
Признаки делимости на 2. Признаки делимости на 5 Признаки делимости на 3 и на 9. Простые числа. Составные числа. Делители натурального числа. Запись числа в виде произведения. Разложение натурального числа на простые множители. Наибольший общий делитель. Нахождение наибольшего общего делителя с помощью разложения па простые множители.
Взаимно-простые числа. Наибольший общий делитель взаимно – простых чисел. Кратные числа. Наименьшее общее кратное.
Наименьшее общее кратное взаимно - простых чисел. Задачи на нахождение наибольшего общего делителя и наименьшего общего кратного.
Использование четности и нечетности при решении задач. Графы. Простые числа. Формула Эйлера
Глава 4. Обыкновенные дроби (75)
Сравнение дробей с разными знаменателями. Сравнение дробей с единицей. Арифметические действия с обыкновенными дробями.
Сложение дробей с одинаковыми знаменателями. Сложение дробей с разными знаменателями. Решение задач на сложение дробей с разными знаменателями. Переместительный закон сложения. Сочетательный закон сложения. Решение задач на сложение дробей. Вычитание дробей с одинаковыми знаменателями. Вычитание дробей с разными знаменателями. Решение задач на сложение и вычитание дробей.
Умножение дроби на натуральное число. Сокращение дробей. Умножение дробей Произведение взаимно – обратных чисел.
Упрощение числовых выражений Законы умножения. Распределительный закон. Деление дроби на натуральное число Деление дробей. Решение задач на деление дробей. Нахождение части целого. Нахождение целого по его части. Задачи на совместную работу.
Задачи на движение. Старинные задачи на совместную работу. Понятие смешанной дроби. Запись смешанного числа в виде неправильной дроби. Выделение целой части неправильной дроби.
Сложение смешанных дробей с одинаковыми знаменателями. Сложение смешанных дробей с разными знаменателями. Вычитание смешанных дробей. Вычитание дроби из натурального числа. Решение упражнений на сложение и вычитание. Умножение смешенного числа на натуральное число. Умножение смешенных чисел. Деление смешанных дробей Деление смешенного числа на натуральное число. Нахождение значений числовых выражений. Представление дроби на координатном луче. Координаты середины отрезка. Среднее результатов измерений.
Среднее арифметическое чисел. Представление зависимости между величинами в виде формул. Прямоугольник. Площадь прямоугольника.
Наглядные представления о пространственных телах: кубе, параллелепипеде. Объем прямоугольного параллелепипеда.
Сложные задачи на движение по реке. Занимательные задачи на дроби Старинные задачи на дроби.
Повторение (20)
Арифметические действия с натуральными числами. Решение задач на арифметические действия с натуральными числами. Признаки делимости Задачи на «части». Действия с обыкновенными дробями. Действия со смешанными числами. Решение задач на дроби.
Задачи на «движение». Задачи на «движение» по реке. Задачи на совместную работу. Прямоугольник, параллелепипед.
На изучение раздела «Элементы комбинаторики, статистики и теории вероятностей» отводится 14 часов, которые распределены следующим образом.
| № п/п | № урока в КТП | Тема учебного материала | Кол-во часов | Календарные сроки |
| 1 | 50 | Занимательные задачи: Круги Эйлера | 1 | 29.10 |
| 2 | 52 | Решение комбинаторных задач: перебор вариантов | 1 | 31.10 |
| 3 | 83 | Представление данных в виде таблицы | 1 | 13.12 |
| 4 | 90 | Представление данных в виде таблицы | 1 | 21.12 |
| 5 | 113 | Графы. Формула Эйлера | 1 | 31.01 |
| 6 | 115 | Решение комбинаторных задач: правило умножения | 1 | 2.02 |
| 7 | 179 | Среднее результатов измерений | 1 | 26.04 |
| 8 | 180 | Среднее арифметическое чисел | 1 | 26.04 |
| 9 | 185 | Представление данных в виде диаграмм | 1 | 3.05 |
| 10 | 187 | Понятие и примеры случайных событий | 1 | 4.05 |
| 11 | 188 | Понятие достоверных, невозможных событий | 1 | 6.05 |
| 12 | 189 | Понятие вероятности случайного события | 1 | 7.05 |
| 13 | 207 | Решение комбинаторных задач | 1 | 28.05 |
| 14 | 208 | Представление данных в виде таблиц и диаграмм | 1 | 29.05 |
Требования к уровню подготовки учащихся 5 класса
В результате изучения курса математики в 5 классе учащиеся должны
знать/понимать:
существо понятия алгоритма, примеры алгоритмов;
как используются математические формулы и уравнения при решении математических и практических задач;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
уметь:
выполнять устно действия сложения и вычитания двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, сложение и вычитание обыкновенных дробей с однозначным числителем и знаменателем;
переходить от одной формы записи чисел к другой, представлять натуральное число в виде обыкновенной дроби, выполнять арифметические действия с натуральными числами, сравнивать натуральные числа; находить в несложных случаях, значения степеней с натуральными показателями и находить значения числовых выражений;
округлять натуральные числа, находить приближенные значения с недостатком и с избытком;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы, через более мелкие и наоборот;
решать текстовые задачи арифметическим способом, включая задачи, связанные с дробями;
определять координату точки координатного луча, строить точки с заданной координатой;
пользоваться языком геометрии для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры, выполнять чертежи по условию задач;
вычислять значения геометрических величин (длин, углов, периметров), площадей основных геометрических фигур и фигур, составленных из них;
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах и на диаграммах; составлять таблицы, строить диаграммы;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
для решения несложных практических задач, в том числе с использованием справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результатов вычислений; проверки результатов вычислений с использованием различных приемов;
описания реальных ситуаций на языке геометрии;
решения практических задач, связанных с нахождением геометрических величин;
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир);
анализа реальных числовых данных, представленных в виде диаграмм и таблиц;
решения практических задач в повседневной деятельности с использованием действий с числами, длин, площадей, времени, скорости
| № |
Изучаемый раздел, тема учебного материала | Кол-во час. | Кол-во час факт | Календарн сроки | Календарн сроки факт | Планируемые результаты | Контрольно – измерительные материалы |
| Знания | Умения | Общие учебные умения, навыки и способы деятельности |
| Глава 1. Натуральные числа и нуль 52 |
| 1 | Ряд натуральных чисел | 1 |
| 1.09 |
|
Знать понятия: ряд натуральных чисел, законы арифметических действий, алгоритмы выполнения арифметических действий, название компонентов арифметических действий, порядок арифметических действий, разряды и классы натуральных чисел
|
Уметь выполнять устно арифметические действия с натуральными числами, сравнивать натуральные числа, решать текстовые задачи с помощью выполнения арифметических действий, определять порядок действий, понимания смысла «больше на… (в…), «меньше на… (в…),
Уметь складывать и вычитать числа столбиком, находить значения числовых выражений |
Самостоятельно организовывать учебную деятельность
Планировать и осуществлять алгоритмическую деятельность
Вести поиск затруднений и находить выход из них |
|
| 2 3 | Десятичная система исчисления. Запись числа в виде суммы разрядных слагаемых | 1
1 |
| 3.09
4.09 |
|
|
| 4 5 | Сравнение натуральных чисел Сравнение единиц измерения | 1 1 |
| 5.09 6.09 |
|
|
| 6 | Арифметические действия над натуральными числами. Сложение натуральных чисел. | 1 |
| 7.09 |
|
|
| 7 8 | Законы арифметических действий: переместительный, сочетательный. Законы сложения | 1
1 |
| 8.09
10.09 |
|
| 9 10 | Вычитание натуральных чисел Компоненты вычитания в уравнениях
| 1 1 |
| 11.09 12.09 |
|
|
| 11 12 13 | Решение текстовых задач арифметическим способом, с помощью сложения. Решение текстовых задач, с помощью вычитания. Решение текстовых задач арифметическим способом, с помощью сложения и вычитания. | 1
1
1 |
| 13.09
14.09
15.09 |
|
|
| 14 | Умножение натуральных чисел | 1 |
| 17.09 |
|
|
| 15 16 | Переместительный закон умножения. Сочетательный закон умножения | 1
1 |
| 18.09
19.09 |
|
| 17 18 | Распределительный закон Вынесение общего множителя за скобки | 1
1 |
| 20.09
21.09 |
|
|
| 19 | Сложение чисел столбиком | 1 |
| 22.09 |
|
|
| 20 21 | Вычитание чисел столбиком Числовые выражения | 1 1 |
| 24.09 25.09 |
|
| 22 | Контрольная работа № 1по теме «Натуральные числа и нуль» | 1 |
| 26.09 |
| К/р |
| 23 24 | Работа над ошибками контрольной работы №1 Умножение чисел столбиком Умножение круглых чисел |
1 1 |
|
27.09 28.09 |
|
|
| 25 | Решение задач на умножение чисел |
1 |
|
29.09 |
|
| 26 27 | Степень с натуральным показателем Запись числа в виде степени | 1 1 |
| 1.10 2.10 |
|
Знать определение степени с натуральным показателем, алгоритмы решения задач на «части»
Знать алгоритм решения задач на нахождение чисел по сумме и разности
Знать римскую нумерацию чисел
|
Уметь делить натуральные числа с остатком, решать задачи на «части», решать текстовые задачи с помощью деления и умножения
Уметь решать задачи на нахождение чисел по их сумме и разности
Уметь решать задачи на переливания, взвешивания, задачи с помощью кругов Эйлера |
Владеть навыками самооценки своей учебной деятельности
Отражать в устной или письменной форме результаты своей деятельности.
Проявлять творчество, передавать содержимое точно, кратко, грамотно
Творчески решать учебные нетиповые задачи
|
|
| 28 29 | Деление нацело Свойство частного | 1 1 |
| 3.10 4.10 |
|
|
| 30 | Свойства деления. Деление суммы на число | 1 |
| 5.10 |
|
| 31 32 | Решение текстовых задач с помощью умножения Решение текстовых задач с помощью деления | 1
1 |
| 6.10
8.10 |
|
|
| 33 | Задачи «на части» | 1 |
| 9.10 |
|
|
| 34 35 | Задачи «на части», если известна сумма | 2
|
| 10.10 11.10 |
|
| 36 37 | Задачи «на части», если известна разность Задачи на сплавы | 1
1 |
| 12.10
13.10 |
|
| 38 | Деление нацело | 1
|
| 15.10 |
|
|
| 39 40 | Деление с остатком Решение задач на деление с остатком | 1 1 |
| 16.10 17.10 |
|
| 41 42 | Числовые выражения, порядок действий в них, использование скобок. Решение задач с помощью числовых выражений | 1
1 |
| 18.10
19.10 |
|
|
| 43 | Контрольная работа № 2 по теме «Натуральные числа и нуль» | 1 |
| 20.10 |
| К/р |
| 44 45 46 47 | Работа над ошибками контрольной работы №2 Задачи на нахождение двух чисел по их сумме и разности Старинные задачи на нахождение двух чисел по их сумме и разности. Задачи на нахождение двух чисел по их сумме и разности при условии равенства результатов. |
2
1
1 |
|
22.10 23.10 24.10
25.10 |
|
|
|
| Дополнения к главе 1 |
|
|
|
|
|
| 48 49 50 51 52
| Вычисления с помощью калькулятора Этапы развития представления о числе. Римская нумерация Занимательные задачи: Круги Эйлера Задачи на переливания, взвешивания Решение комбинаторных задач: перебор вариантов |
1
1 1 1
1
|
|
26.10
27.10 29.10 30.10
31.10 |
|
| Глава 2. Измерение величин 38 |
| 53 54 | Точка. Прямая. Луч. Отрезок. Параллельные и пересекающиеся прямые | 1 1 |
| 8.11
9.11 |
| Знать понятие прямой, отрезка, луча, единицы измерения отрезков
Знать определения окружности и круга, радиуса, диаметра, дуги, хорды. Понятие сферы, шара Знать определения угла, смежных, вертикальных углов, определение треугольника, виды треугольников: равнобедренные, равносторонние Знать формулы площади прямоугольника, объема параллелепипеда, единицы измерения площадей и объемов
| Уметь измерять и строить отрезки.
Уметь пользоваться формулами при решении задач, согласно условиям задач переходить от одних единиц измерения к другим.
Уметь вычислять смежные и вертикальные углы
Уметь вычислять периметр треугольника, площадь прямоугольника, объём прямоугольного параллелепипеда | Умение разделять процессы на этапы
Самостоятельно составлять формулы
Уметь выбирать и использовать необходимые формулы
|
|
| 55 56 | Измерение отрезков. Расстояние между точками | 1 1 |
| 10.11 12.11 |
|
|
| 57 58 | Метрические единицы измерения длины Запись измерения с недостатком, с избытком | 1
1 |
| 13.11
14.11 |
|
|
| 59 60 | Изображение натуральных чисел точками на координатном луче Определение координат точек на координатном луче | 1
1 |
| 15.11
16.11 |
|
|
| 61 | Контрольная работа № 3 по теме «Измерение величин» | 1 |
| 17.11 |
| К/р |
| 62
63 | Работа над ошибками контрольной работы №3 Геометрические фигуры и некоторые тела. Окружность и круг: центр, радиус, диаметр, дуга, хорда. Сфера и шар. | 1
1 |
|
19.11
20.11 |
|
|
| 64 | Углы. Прямой угол. Острые и тупые углы. | 1
|
| 21.11 |
|
|
| 65 | Измерение углов. Смежные и вертикальные углы | 1 |
|
22.11 |
|
| 66 | Виды треугольников: равнобедренные, равносторонние. | 1 |
|
23.11 |
|
|
| 67 68 | Периметр треугольника Вычисление сторон треугольника | 1 1 |
| 24.11 26.11 |
|
| 69 | Четырехугольники | 1 |
| 27.11 |
|
|
| 70 71 | Периметр четырехугольника Ромб | 1 1 |
| 28.11 29.11 |
|
| 72 73 | Площадь прямоугольника. Площадь квадрата | 1 1 |
| 30.11 1.12 |
|
|
| 74 | Единицы измерения площади | 1 |
| 3.12 |
|
| 75 76 | Прямоугольный параллелепипед Куб. Развертка куба | 1 1 |
| 4.12 5.12 |
|
|
| 77 78 | Объём прямоугольного параллелепипеда Объем куба | 1 1 |
| 6.12 7.12 |
|
|
| 79 | Единицы измерения объёма. | 1 |
| 8.12 |
|
| 80 | Контрольная работа № 4 по теме « Измерение величин»
| 1 |
|
10.12 |
|
|
|
|
| 81 | Работа над ошибками контрольной работы №4 Единицы измерения массы | 1 |
|
11.12 |
|
Знать алгоритмы решения задач на движение, единицы времени, скорости, пути, массы
|
|
Уметь вступать в речевое общение
Творчески решать учебные задачи
|
|
|
Уметь решать задачи на движение, переводить одни единицы измерения в другие, находить периметр многоугольника |
|
| 82 | Единицы измерения времени, длительность процессов в окружающем мире. | 1 |
|
12.12 |
|
|
| 83 | Представление данных в виде таблицы . Задачи на движение | 1 |
|
13.12 |
|
|
| 84 | Движение по реке. | 1 |
| 14.12 |
|
| 85 86 | Единицы измерения скорости. Скорость удаления, скорость сближения. | 1 1 |
| 15.12
17.12 |
|
|
| Дополнение к главе 2 |
|
|
|
|
|
| 87 88 | Многоугольники: замкнутые, выпуклые, равные. Длина ломаной. Периметр прямоугольника | 1
1 |
| 18.12
19.12 |
|
|
| 89 90 | Занимательные задачи на разрезание отрезков, прямоугольников. Представление данных в виде таблицы | 1 1 |
|
20.12 21.12 |
|
| Глава3. Делимость натуральных чисел 25 |
| 91 92 93 | Делимость натуральных чисел Свойства делимости суммы Свойства делимости произведения | 1 1 1 |
| 22.12 24.12 25.12 |
| Знать понятия простые и составные числа, взаимно-простые числа, признаки делимости | Уметь применять признаки делимости
Уметь применять признаки делимости при разложении на простые множители |
Уметь сравнивать, обобщать, делать логический вывод.
|
|
| 94 95 | Признаки делимости на 2 Признаки делимости на 5 | 1 1
|
| 26.12 27.12 |
|
|
| 96 97 | Признаки делимости на 3 и 9 Признак делимости на 4 | 1 1 |
| 28.12 29.12 |
|
| 98 99 | Простые числа Составные числа | 1 1 |
| 14.01 15.01
|
|
|
| 100 | Делители натурального числа | 1 |
| 16.01 |
|
|
| 101 102 | Запись числа в виде произведения Разложение натурального числа на простые множители | 1 1 |
| 17.01 18.01 |
|
| 103 104 | Наибольший общий делитель Нахождение наибольшего общего делителя с помощью разложения на простые множители | 1
1 |
| 19.01
21.01 |
|
Знать определения взаимно-простых чисел, делителя , кратного, алгоритм нахождения НОД и НОК |
Уметь раскладывать числа на простые множители, находить НОД и НОК, решать задачи на НОД и НОК |
Выполнять и конструировать новые алгоритмы |
|
| 105 106 | Взаимно-простые числа Наибольший общий делитель взаимно – простых чисел | 1 1 |
| 22.01 23.01 |
|
| 107 108 | Кратные числа Наименьшее общее кратное | 1 1 |
| 24.01 25.01 |
|
|
| 109 110 | Наименьшее общее кратное взаимно - простых чисел Задачи на нахождение наибольшего общего делителя и наименьшего общего кратного | 1
1 |
| 26.01
28.01 |
|
| 111 | Контрольная работа № 5 по теме «Делимость натуральных чисел» | 1 |
| 29.01 |
| К\р |
|
| Дополнения к главе 3 |
|
|
|
|
|
| 112 113 | Работа над ошибками контрольной работы №5 Использование четности и нечетности при решении задач. Графы. Формула Эйлера |
1
1 |
|
30.01
31.01 |
|
|
| 114
115 | Занимательные задачи Решение комбинаторных задач: правило умножения | 1
1 |
| 1.02
2.02 |
|
|
| Глава 4. Обыкновенные дроби 75 |
| 116 117 118 | Обыкновенная дробь. Основное свойство дроби Равенство дробей | 1 1 1 |
| 4.02 5.02 6.02 |
|
Знать основное свойство дроби
Знать основные задачи на дроби, алгоритмы сравнения, сложения и вычитания обыкновенных дробей
Знать порядок арифметических действий чисел, законы сложения и вычитания Знать алгоритмы сложения и вычитания дробей с разными знаменателями
Знать алгоритм сокращения, умножения, деления дробей, решения задач на совместную работу
Знать алгоритмы выделения целой части , запись смешанной дроби в виде неправильной дроби, сложения и вычитания смешанных дробей
Знать алгоритмы умножения и деления смешанных дробей
Знать формулы нахождения среднего арифметического чисел Знать формулы площади прямоугольника, объема параллелепипеда |
Уметь сравнивать дроби, сокращать дроби, приводить дроби к новому знаменателю, решать основные задачи на дроби
Выполнять арифметические действия с обыкновенными дробями
Уметь умножать, делить обыкновенные дроби. Уметь решать задачи на действия с обыкновенными дробями, на совместную работу
Уметь складывать и вычитать смешанные дроби, выделять целую часть, смешанную дробь записывать в виде неправильной дроби
Уметь умножать и делить смешанные дроби
|
Планировать и осуществлять алгоритмическую деятельность
Выдвигать гипотезу предположение, формулировать выводы
Использовать различные языки математики, свободно переходить с одного языка на другой
Решать задач требующие поиска пути и способов решения
Классифициро - вать и выбирать способ действий
Планировать и осуществлять алгоритмическую деятельность
Использовать и самостоятельно составлять формулы
|
|
| 119 | Сокращение дробей | 1 |
| 7.02 |
|
| 120 121 | Нахождение части от целого (дроби от числа) Задачи на нахождение части от целого (дроби от числа) |
1
1
|
|
8.02
9.02 |
|
|
| 122 123 124 | Нахождение целого по его части (числа по дроби) Задачи на нахождение целого по его части (числа по дроби) Старинные задачи на нахождение части от целого, целого по его части
| 1
1
1 |
| 11.02
12.02
13.02 |
|
| 125 126 | Алгоритм приведение дроби к новому знаменателю Приведение дроби к новому знаменателю | 1
1 |
| 14.02
15.02 |
|
|
| 127 128 | Общий знаменатель дробей Приведение дробей к общему знаменателю | 1 1 |
| 16.02 18.02 |
|
| 129 | Сравнение дробей с одинаковыми знаменателями | 1
|
| 19.02 |
|
|
| 130 131 | Сравнение дробей с разными знаменателями Сравнение дробей с единицей | 1
1 |
| 20.02
21.02 |
|
| 132 | Арифметические действия с обыкновенными дробями Сложение дробей с одинаковыми знаменателями |
1
|
|
22.02 |
|
|
| 133 134 | Сложение дробей с разными знаменателями Решение задач на сложение дробей с разными знаменателями | 1
1 |
| 25.02
26.02 |
|
| 135 136 | Переместительный закон сложения Сочетательный закон сложения | 1 1 |
| 27.02 28.02 |
|
|
| 137 138 | Решение задач на сложение дробей с одинаковыми знаменателями Решение задач на сложение дробей с разными знаменателями | 1
1 |
| 1.03
2.03 |
|
| 139 140 | Вычитание дробей с одинаковыми знаменателями. Вычитание дробей с разными знаменателями | 1
1 |
| 4.03
5.03 |
|
|
| 141 142 | Решение задач на сложение и вычитание дробей | 1 1 |
| 6.03 7.03 |
|
| 143 | Контрольная работа № 6 по теме «Обыкновенные дроби» | 1 |
| 9.03 |
| К\р |
| 144 145 | Работа над ошибками контрольной работы №6 Умножение дроби на натуральное число Сокращение дробей | 1
1 |
| 11.03
12.03 |
|
|
| 146 147 | Умножение дробей Произведение взаимно – обратных чисел Упрощение числовых выражений | 1
1 |
| 13.03
14.03 |
|
| 148 149 | Законы умножения. Распределительный закон | 1 1 |
| 15.03 16.03 |
|
|
| 150 151 | Деление дроби на натуральное число Деление натурального числа на дробь | 1 1 |
| 18.03 19.03 |
|
|
| 152 153 | Деление дробей Решение задач на деление дробей | 1 1 |
| 20.03 21.03 |
|
| 154 155 | Нахождение части целого Нахождение целого по его части | 1 1 |
| 22.03 1.04 |
|
|
| 156 | Задачи на совместную работу | 1 |
| 2.04 |
|
|
| 157 158 159 | Задачи на совместную работу при одновременной работе труб Задачи на движение Задачи на прохождения некоторого пути. | 1 1 1 |
|
3.04 4.04 5.04 |
|
|
| 161
162 163 | Понятие смешанной дроби Запись смешанного числа в виде неправильной дроби Выделение целой части | 1 1
1 |
| 6.04 8.04
9.04 |
|
|
| 164
165
166 | Сложение смешанных дробей с натуральными числами Сложение смешанных дробей с одинаковыми знаменателями Сложение смешанных дробей с разными знаменателями | 1
1
1 |
| 10.04
11.04
12.04 |
|
|
| 167
168
169 | Вычитание смешанных дробей с одинаковыми знаменателями Вычитание дроби из натурального числа Вычитание смешанных дробей с разными знаменателями
| 1
1
1 |
| 13.04
15.04
16.04 |
|
|
| 170 | Решение упражнений на сложение и вычитание смешанных дробей | 1 |
| 17.04 |
|
| 171 172 | Умножение смешанного числа на натуральное число Умножение смешанных чисел
| 1
1 |
| 18.04
19.04 |
|
|
| 173 174 175 | Деление смешанных дробей Деление смешанного числа на натуральное число Нахождение значений числовых выражений | 1 1
1 |
| 20.04 22.04
23.04 |
|
|
|
| 176 | Контрольная работа № 7 по теме «Обыкновенные дроби» | 1 |
| 24.04 |
| К\р |
| 177
178 | Работа над ошибками контрольной работы №7 Представление дроби на координатном луче Координаты середины отрезка | 1
1
|
|
25.04
25.04 |
|
|
| 179 180 | Среднее результатов измерений Среднее арифметическое чисел | 1 1 |
| 26.04 26.04 |
|
| 181 | Представление зависимости между величинами в виде формул Прямоугольник. Площадь прямоугольника. |
1
|
|
27.04 |
|
|
| 182
183 | Наглядные представления о пространственных телах: кубе, параллелепипеде. Объем прямоугольного параллелепипеда |
1
1 |
|
29.04
30.04 |
|
|
| Дополнения к главе 4 |
|
|
|
|
|
|
| 184 | Сложные задачи на движение по реке | 1
|
| 2.05 |
|
|
|
|
|
| 185 186 187 188 189
|
Представление данных в виде диаграмм Занимательные задачи на дроби Понятия и примеры случайных событий Понятия достоверных, невозможных событий Понятие вероятности случайного события
|
1
1 1
1
1 |
|
3.05
3.05 4.05
6.05
7.05 |
|
Знать формулу нахождения вероятности случайного события |
|
Логически обосновывать выводы на математическом языке
|
|
| Повторение 20 |
| 190 191
192 | Арифметические действия с натуральными числами Решение задач на арифметические действия с натуральными числами Решение задач на арифметические действия с натуральными числами | 1
1
1 |
| 8.05
10.05
11.05 |
|
Знать изученные определения, формулы, алгоритмы | Уметь применять изученные определения, формулы, алгоритмы | Понимать ценность образования как средства развития личности
Анализировать, обобщать и систематизир. информацию |
|
| 193 | Признаки делимости | 1 |
| 13.05 |
|
| 194 195 | Задачи на «части» , если известна сумма Задачи на «части», если известна разность | 1
1 |
| 14.05
15.05 |
|
| 196 197 198 | Действия с обыкновенными дробями Действия со смешанными числами Решение задач на дроби | 1 1 1 |
| 16.05 17.05 17.05 |
|
| 199 200 201 | Задачи на «движение» в одном направлении Задачи на «движение» навстречу друг к другу Задачи на «движение» по реке | 1 1
1 |
| 18.05 20.05
21.05
22.05 23.05
24.05 25.05
27.05 28.05 29.05 30.05 31.05 |
|
| 202 203 | Задачи на совместную работу при одновременной работе труб Задачи на движение, прохождения некоторого пути. |
1 1 |
|
|
| 204 205 | Итоговая контрольная работа №8 Прямоугольник Параллелепипед |
1 1
|
|
|
| 206 207 208
209 210 | Параллелепипед Решение комбинаторных задач Представление данных в виде таблиц и диаграмм Решение задач | 1 1
1
2 |
|
| Итог. к/р |
Критерии и нормы оценки знаний, умений и навыков обучающихся по математике.
Рекомендации по оценке знаний, умений и навыков учащихся по математике.
Опираясь на эти рекомендации, учитель оценивает знания, умения и навыки учащихся с учетом их индивидуальных особенностей.
Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
Основными формами проверки знаний и умений, учащихся по математике являются письменная контрольная работа и устный опрос.
Среди погрешностей выделяются ошибки и недочеты.
Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями, указанными в программе.
К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, которые в программе не считаются основными. Недочетами также считаются: погрешности, которые не привели к искажению смысла полученного учеником задания или способа его выполнения: неаккуратная запись, небрежное выполнение чертежа.
Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.
Ответ на теоретический вопрос считается безупречным, если по своему содержанию полностью соответствует вопросу, содержит все необходимые теоретические факты и обоснованные выводы, а его изложение и письменная запись математически грамотны и отличаются последовательностью и аккуратностью.
Решение задачи считается безупречным, если правильно выбран способ решения, само решение сопровождается необходимыми объяснениями, верно, выполнены нужные вычисления и преобразования, получен верный ответ, последовательно и аккуратно записано решение.
Оценка ответа учащихся при устном и письменном опросе производится по 4-х балльной («5», «4», «3», «2») системе.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии учащегося, за решение более сложной задачи или ответ на более сложный вопрос, предложенные учащемуся дополнительно после выполнения им задания.
Итоговые отметки (за тему, четверть, курс) выставляются по состоянию знаний на конец этапа обучения с учетом текущих отметок.
Оценка устных ответов учащихся.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком в определенной логической последовательности, точно используя математическую терминологию и символику;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой ситуации при выполнении практического задания;
продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость использованных при ответе умений и навыков;
отвечал самостоятельно без наводящих вопросов учителя.
Возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Ответ оценивается отметкой «4», если он удовлетворен в основном требованиям на отметку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившие математического содержания ответа, исправленные по замечанию учителя.
допущены ошибки или более двух недочетов при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.
Отметка «3» ставится в следующих случаях:
неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке учащихся»).
имелись затруднения или допущены ошибки в определении понятий и, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при знании теоретического материала выявлена недостаточная сформированность умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Оценка письменных контрольных работ учащихся.
Отметка «5» ставится в следующих случаях:
работа выполнена полностью.
в логических рассуждениях и обоснованиях нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала);
Отметка «4» ставится, если:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умения обосновывать рассуждения не являлись специальным объектом проверки);
допущена одна ошибка или два-три недочета в выкладках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки);
Отметка «3» ставится, если:
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что учащийся не владеет обязательными знаниями по данной теме в полной мере;
работа показала полное отсутствие у учащегося обязательных знаний, умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
График поведения плановых контрольных работ
по математике в 5 Г классе
в 2012 – 2013 учебном году.
| Дата проведения | Предмет | Класс | Вид контроля |
| 26.09 | математика | 5 Г | Контрольная работа № 1 по теме: «Натуральные числа и нуль»
|
| 20.10 | математика |
| Контрольная работа № 2 по теме: «Натуральные числа и нуль»
|
| 17.11 | математика |
| Контрольная работа № 3 по теме: «Измерение величин»
|
| 10.12 | математика |
| Контрольная работа № 4 по теме: «Измерение величин»
|
| 29.01 | математика |
| Контрольная работа № 5 по теме: «Делимость натуральных чисел»
|
| 9.03 | математика |
| Контрольная работа № 6 по теме: «Обыкновенные дроби»
|
| 24.04 | математика |
| Контрольная работа № 7 по теме: «Обыкновенные дроби»
|
| 24.05
| математика |
| Итоговая контрольная работа № 8
|
|
Литература и средства обучения. |
|
|
|
|
Математика. Дидактические материалы. 5 класс /М.К. Потапов, А.В. Шевкин – М.: Просвещение , 2012 / Математика. 5 класс. Рабочая тетрадь. Пособие для учащихся общеобразовательных учреждений в двух частях / М.К. Потапов, А.В. Шевкин – М.: Просвещение , 2012 / Тематические тесты. Математика 5 класс /П.В. Чулков – М.: Просвещение, 2012/ Математика. Тесты для промежуточной аттестации учащихся 5-6 классов. /Ф.Ф. Лысенко – Ростов-на-Дону: Легион, 2007/ http://www.uchportal.ru/load/25
|
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход











 Рабочая программа по математике (5 класс) (0.52 MB)
Рабочая программа по математике (5 класс) (0.52 MB)
 0
0 875
875 198
198 Нравится
0
Нравится
0




