МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 126
Кировского района городского округа город Уфа РБ
| РАССМОТРЕНО Руководитель МО ___________ /Хисматова Л.Р/ Протокол _____ от «____»_____________20 ___г. | СОГЛАСОВАНО Зам. директора по УВР ___________ /Гоголева И.А./ «___»______________20___г. | УТВЕРЖДАЮ Директор МБОУ СОШ № 126 ____________/Фархтдинова Г.Ю./ Приказ № ____от «___»______________20___г. |
РАБОЧАЯ ПРОГРАММА
по учебному предмету
«Математика»
для учащихся 3 класса
Разработчик:
учитель Нагуманова
Нурия Альбертовна
(высшая квалификационная
категория)
Уфа – 2013
СОДЕРЖАНИЕ
Пояснительная записка………………………………………..…...3 Общая характеристика учебного предмета………….……….......6 Описание места учебного предмета в учебном плане……………………………………………………..............16 Описание ценностных ориентиров содержания учебного предмета……………………………………………..…….................16 Личностные, метапредметные и предметные результаты освоения учебного предмета…………………………..…….…….....18 Содержание тем учебного предмета………………………….....26 Тематическое планирование и основные виды деятельности учащихся………………………………….…..…38 Материально-техническое обеспечение образовательного процесса…………………………………………….……….….56
|
РАБОЧА ПРОГРАММА ПО МАТЕМАТИКЕ
для 3-го класса начальной школы
I. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа курса «Математика» разработана на основе Федерального государственного образовательного стандарта начального общего образования, Концепции духовно-нравственного развития и воспитания личности гражданина России, планируемых результатов начального общего образования с учетом межпредметных и внутрипредметных связей, логики учебного процесса, задачи формирования у младших школьников умения учиться, а также на основе авторской программы «Математика» , разработанной Л.Г. Петерсон и др., которая является составной частью Образовательной системы «Перспектива» и разработана с учетом межпредметных и внутрипредметных связей, логики учебного процесса по литературному чтению, возрастных особенностей младших школьников.
Назначение предмета «Математика» в начальной школе состоит в том, чтобы заложить основу формирования функционально грамотной личности, владеющей системой математических знаний для решения практических жизненных задач, а так же обеспечить языковое и речевое развитие ребёнка через первоначальное овладение математическим языком.
Выбор данной авторской программы и учебно-методического комплекса обусловлен тем, что содержание авторской программы и логика изложения программного материала в учебнике «Математика. 3 класс» полностью соответствуют требованиям федерального компонента государственного стандарта начального образования.
Основными целями курса математики для 1–4 классов, в соответствии с требованиями ФГОС НОО, являются:
формирование у учащихся основ умения учиться;
развитие их мышления, качеств личности, интереса к математике;
создание для каждого ребенка возможности высокого уровня математической подготовки.
Соответственно задачами данного курса являются:
формирование у учащихся способностей к организации своей учебной деятельности посредством освоения личностных, познавательных, регулятивных и коммуникативных универсальных учебных действий;
приобретение опыта самостоятельной математической деятельности по получению нового знания, его преобразованию и применению;
формирование специфических для математики качеств мышления, необходимых человеку для полноценного функционирования в современном обществе, и в частности, логического, алгоритмического и эвристического мышления;
духовно-нравственное развитие личности, предусматривающее, с учетом специфики начального этапа обучения математике, принятие нравственных установок созидания, справедливости, добра, становление основ гражданской российской идентичности, любви и уважения к своему Отечеству;
формирование математического языка и математического аппарата как средства описания и исследования окружающего мира и как основы компьютерной грамотности;
реализация возможностей математики в формировании научного мировоззрения учащихся, в освоении ими научной картины мира с учетом возрастных особенностей учащихся;
овладение системой математических знаний, умений и навыков, необходимых для повседневной жизни и для продолжения образования в средней школе;
создание здоровьесберегающей информационно-образовательной среды.
Данная программа составлена для реализации курса математики, который является частью курса математики для дошкольников, начальной школы и 5−6 классов средней школы образовательной системы «Школа 2000...» и, таким образом, обеспечивает преемственность математической подготовки между ступенями дошкольного, начального и общего среднего образования. Предметные знания и умения, приобретённые при изучении математики в начальной школе, первоначальное овладение математическим языком являются опорой для изучения смежных дисциплин, фундаментом обучения в старших классах общеобразовательных учреждений.
В то же время в начальной школе этот предмет является основой развития у учащихся познавательных действий, в первую очередь логических, включая и знаково-символические, а также таких, как планирование (цепочки действий по задачам), систематизация и структурирование знаний, преобразование информации, моделирование, дифференциация существенных и несущественных условий, аксиоматика, формирование элементов системного мышления, выработка вычислительных навыков. Особое значение имеет математика для формирования общего приема решения задач как универсального учебного действия. Таким образом, математика является эффективным средством развития личности школьника.
Исходя из общих положений концепции математического образования, начальный курс математики призван решать следующие задачи:
- создать условия для формирования логического и абстрактного мышления у младших школьников на входе в основную школу как основы их дальнейшего эффективного обучения;
сформировать набор необходимых для дальнейшего обучения предметных и общеучебных умений на основе решения как предметных, так и интегрированных жизненных задач;
обеспечить прочное и сознательное овладение системой математических знаний и умений, необходимых для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования; обеспечить интеллектуальное развитие, сформировать качества мышления, характерные для математической деятельности и необходимые для полноценной жизни в обществе;
сформировать представление об идеях и методах математики, о математике как форме описания и методе познания окружающего мира;
сформировать представление о математике как части общечеловеческой культуры, понимание значимости математики для общественного прогресса;
сформировать устойчивый интерес к математике на основе дифференцированного подхода к учащимся;
выявить и развить математические и творческие способности на основе заданий, носящих нестандартный, занимательный характер.
Для формирования определённых ФГОС НОО универсальных учебных действий (УУД) как основы умения учиться предусмотрено системное прохождение каждым учащимся основных этапов формирования любого умения, а именно:
приобретение опыта выполнения УУД;
мотивация и построение общего способа (алгоритма) выполнения УУД (или структуры учебной деятельности);
тренинг в применении построенного алгоритма УУД, самоконтроль и коррекция;
контроль.
На первом из перечисленных этапов формирования УУД уроки проводятся по технологии деятельностного метода «Школа 2100...» (ТДМ). Дети не получают знания в готовом виде, а добывают их в процессе собственной учебной деятельности. При этом обеспечивается возможность выполнения ими всего комплекса личностных, регулятивных, познавательных и коммуникативных универсальных учебных действий, предусмотренных ФГОС.
На основе приобретённого опыта учащиеся строят общий способ выполнения УУД (второй этап). После этого они применяют построенный общий способ, проводят самоконтроль и при необходимости коррекцию своих действий (третий этап). И наконец, по мере освоения УУД проводится контроль данного УУД и умения учиться в целом (четвёртый этап).
Использование деятельностного метода обучения позволяет при изучении всех разделов данного курса организовать полноценную математическую деятельность учащихся с целью получения нового знания, его преобразования и применения, включающую три основных этапа математического моделирования:
этап построения математической модели некоторого объекта или процесса реального мира;
этап изучения математической модели средствами математики;
этап приложения полученных результатов к реальному миру.
На ступени начального общего образования этот учебный предмет является основой развития у обучающихся познавательных универсальных действий, в первую очередь логических и алгоритмических. В процессе знакомства с математическими отношениями, зависимостями у школьников формируются учебные действия планирования последовательности шагов при решении задач; различения способа и результата действия; выбора способа достижения поставленной цели; использования знаково-символических средств для моделирования математической ситуации, представления информации; сравнения и классификации (например, предметов, чисел, геометрических фигур) по существенному основанию.
Содержание курса целенаправленно формирует информационную грамотность, умение самостоятельно получать информацию из наблюдений, бесед, справочников, энциклопедий, Интернета и работать с полученной информацией.
Новизна данной программы определяется тем, что предполагает осуществлять индивидуальный контроль за формированием предметных и метапредмтеных компетенций, пользуясь новой системой оценки планируемых результатов.
При организации процесса обучения в рамках данной программы предполагается применением следующих педагогических технологий обучения:
• дидактической системы деятельностного метода «Школа 2100...» (Л.Г. Петерсон);
• проблемно-диалогического обучения;
• технология коллективного способа обучения;
• технология оценивания образовательных достижений;
• Технология проектной деятельности.
Промежуточная аттестация проводится в соответствии с Уставом ОУ, проводится в форме итоговых контрольных, переводных и диагностических работ.
Срок реализации программы – 1 год.
II. ОБЩАЯ ХАРАКТЕРИСТИКА КУРСА
Данный курс создан на основе личностно ориентированных, деятельностно ориентированных и культурно ориентированных принципов, сформулированных в образовательной программе «Школа 2100», основной целью которой является формирование функционально грамотной личности, готовой к активной деятельности и непрерывному образованию в современном обществе, владеющей системой математических знаний и умений, позволяющих применять эти знания для решения практических жизненных задач, руководствуясь при этом идейно-нравственными, культурными и этическими принципами, нормами поведения, которые формируются в ходе учебно-воспитательного процесса.
Содержание курса математики строится на основе:
− системно-деятельностного подхода, методологическим основанием
которого является общая теория деятельности (Л.С. Выготский, А.Н. Леонтьев, Г.П. Щедровицкий, О.С. Анисимов и др.);
− системного подхода к отбору содержания и последовательности
изучения математических понятий, где в качестве теоретического основания выбрана Система начальных математических понятий (Н.Я. Виленкин);
− дидактической системы деятельностного метода «Школа
2000...» (Л.Г. Петерсон).
Педагогическим инструментом реализации поставленных целей в
курсе математики является дидактическая система деятельностного метода «Школа 2000...»…3. Суть ее заключается в том, что учащиеся не получают знания в готовом виде, а добывают их сами в процессе собственной учебной деятельности. В результате школьники приобретают личный опыт математической деятельности и осваивают систему знаний по математике, лежащих в основе современной научной картины мира. Но, главное, они осваивают весь комплекс универсальных учебных действий (УУД), определенных ФГОС, и умение учиться в целом.
Основой организации образовательного процесса в дидактической
системе «Школа 2000...» является технология деятельностного метода (ТДМ), которая помогает учителю включить учащихся в самостоятельную учебно-познавательную деятельность.
Структура ТДМ, с одной стороны, отражает обоснованную в методологии общую структуру учебной деятельности (Г.П. Щедровицкий, О.С. Анисимов и др.), а с другой стороны, обеспечивает преемственность с традиционной школой в формировании у учащихся глубоких и прочных знаний, умений и навыков по математике. Например, структура уроков по ТДМ, на которых
учащиеся открывают новое знание, имеет вид:
1. Мотивация к учебной деятельности.
Данный этап процесса обучения предполагает осознанное вхождение
учащихся в пространство учебной деятельности на уроке. С этой целью организуется их мотивирование на основе механизма «надо» − «хочу» − «могу».
2. Актуализация и фиксирование индивидуального затруднения в
пробном учебном действии. На данном этапе организуется подготовка учащихся к открытию нового знания, выполнение ими пробного учебного действия, фиксация индивидуального затруднения. Завершение этапа связано с организацией обдумывания учащимися возникшей проблемной ситуации.
3. Выявление места и причины затруднения.
На данном этапе учитель организует выявление учащимися места и причины возникшего затруднения на основе анализа проблемной ситуации.
4. Построение проекта выхода из затруднения.
Учащиеся в коммуникативной форме обдумывают проект будущих
учебных действий: ставят цель, формулируют тему, выбирают способ,
строят план достижения цели и определяют средства. Этим процессом руководит учитель.
5. Реализация построенного проекта.
На данном этапе осуществляется реализация построенного проекта:
обсуждаются различные варианты, предложенные учащимися, и выбирается оптимальный вариант, который фиксируется вербально и знаково (в форме эталона). Построенный способ действий используется для решения исходной задачи, вызвавшей затруднение. В завершение уточняется общий характер нового знания и фиксируется преодоление возникшего затруднения.
6. Первичное закрепление с проговариванием во внешней речи.
На данном этапе учащиеся в форме коммуникативного взаимодействия (фронтально, в парах, в группах) решают типовые задания на новый способ действий с проговариванием алгоритма решения вслух.
7. Самостоятельная работа с самопроверкой по эталону.
При проведении данного этапа используется индивидуальная форма работы: учащиеся самостоятельно выполняют задания нового типа и осуществляют их самопроверку, пошагово сравнивая с эталоном. В завершение организуется рефлексия хода реализации построенного проекта и контрольных процедур.
Эмоциональная направленность этапа состоит в организации для
каждого ученика ситуации успеха, мотивирующей его к включению в дальнейшую познавательную деятельность.
8. Включение в систему знаний и повторение.
На данном этапе выявляются границы применимости нового знания и
выполняются задания, в которых новый способ действий предусматривается как промежуточный шаг. Таким образом, происходит, с одной стороны, формирование навыка применения изученных способов действий, а с другой –
подготовка к введению в будущем следующих тем.
9. Рефлексия учебной деятельности на уроке (итог урока).
На данном этапе фиксируется новое содержание, изученное на уроке, и организуется рефлексия и самооценка учениками собственной учебной деятельности. В завершение соотносятся поставленная цель и результаты, фиксируется степень их соответствия, и намечаются дальнейшие цели деятельности.
Данная структура урока может быть представлена следующей схемой, позволяющей в наглядном виде соотнести этапы урока по ТДМ с методом рефлексивной самоорганизации.
Технология деятельностного метода «Школа 2000...» (ТДМ)
Помимо уроков открытия нового знания, в дидактической системе
«Школа 2000...» имеются уроки других типов:
уроки рефлексии, где учащиеся закрепляют свое умение применять новые способы действий в нестандартных условиях, учатся самостоятельно выявлять и исправлять свои ошибки, корректируют свою учебную деятельность;
уроки обучающего контроля, на которых учащиеся учатся контролировать результаты своей учебной деятельности;
уроки систематизации знаний, предполагающие структурирова-ние и систематизацию знаний по изучаемым предметам.
Все уроки также строятся на основе метода рефлексивной самоорганизации, что обеспечивает возможность системного выполнения каждым ребенком всего комплекса личностных, регулятивных, познавательных и коммуникативных универсальных учебных действий, предусмотренных ФГОС.
Технология деятельностного метода обучения может использоваться в образовательном процессе на разных уровнях в зависимости от предметного содержания урока, поставленных дидактических задач и уровня освоения учителем метода рефлексивной самоорганизации: базовом, технологическом и системно-технологическом.
Базовый уровень ТДМ включает в себя следующие шаги:
1) Мотивация к учебной деятельности.
2) Актуализация знаний.
3) Проблемное объяснение нового знания.
4) Первичное закрепление во внешней речи.
5) Самостоятельная работа с самопроверкой.
6) Включение нового знания в систему знаний и повторение.
7) Рефлексия учебной деятельности на уроке.
Структура урока базового уровня выделяет из общей структуры рефлексивной самоорганизации ту ее часть, которая представляет собой целостный элемент. Таким образом, не вступая в противоречие со структурой деятельностного метода обучения, базовый уровень ТДМ систематизирует инновационный опыт российской школы об активизации деятельности детей в процессе трансляции системы знаний. Поэтому базовый уровень ТДМ используется также как ступень перехода учителя от традиционного объяснительно-иллюстративного метода к деятельностному методу.
На технологическом уровне при введении нового знания учитель начинает использовать уже целостную структуру ТДМ, однако построение самими детьми нового способа действия организуется пока еще с отсутствием существенных компонентов (этап проектирования и реализации проекта).
На системно-технологическом уровне деятельностный метод реализуется в его полноте.
Для формирования определенных ФГОС НОО универсальных учебных действий как основы умения учиться предусмотрена возможность системного прохождения каждым учащимся основных этапов формирования любого умения, а именно:
1. Приобретение опыта выполнения УУД.
2. Мотивация и построение общего способа (алгоритма) выполнения
УУД (или структуры учебной деятельности).
3. Тренинг в применении построенного алгоритма УУД, самоконтроль
и коррекция.
4. Контроль.
На уроках по ТДМ «Школа 2000...» учащиеся приобретают первичный
опыт выполнения УУД. На основе приобретенного опыта они строят общий способ выполнения УУД (второй этап). После этого они применяют построенный общий способ, проводят самоконтроль и, при необходимости, коррекцию своих действий (третий этап). И, наконец, по мере освоения данного УУД и умения учиться в целом проводится контроль реализации требований ФГОС (четвертый этап)4.
Создание информационно-образовательной среды осуществляется на
основе системы дидактических принципов деятельностного метода обучения «Школа 2000...»:
1) Принцип деятельности – заключается в том, что ученик, получая
знания не в готовом виде, а, добывая их сам, осознает при этом содержание и формы своей учебной деятельности, понимает и принимает систему ее норм, активно участвует в их совершенствовании, что способствует активному успешному формированию его общекультурных и деятельностных способностей, общеучебных умений.
2) Принцип непрерывности – означает преемственность между всеми
ступенями и этапами обучения на уровне технологии, содержания и методик с учетом возрастных психологических особенностей развития детей.
3) Принцип целостности – предполагает формирование у учащихся
обобщенного системного представления о мире (природе, обществе, самом себе, социокультурном мире и мире деятельности, о роли и месте каждой науки в системе наук, а также роли ИКТ).
4) Принцип минимакса – заключается в следующем: школа должна
предложить ученику возможность освоения содержания образования на максимальном для него уровне (определяемом зоной ближайшего развития возрастной группы) и обеспечить при этом его усвоение на уровне социально безопасного минимума (федерального государственного образовательного стандарта).
5) Принцип психологической комфортности – предполагает снятие
всех стрессообразующих факторов учебного процесса, создание в школе и на уроках доброжелательной атмосферы, ориентированной на реализацию идей педагогики сотрудничества, развитие диалоговых форм общения.
6) Принцип вариативности – предполагает формирование у учащихся
способностей к систематическому перебору вариантов и адекватному принятию решений в ситуациях выбора.
7) Принцип творчества – означает максимальную ориентацию на творческое начало в образовательном процессе, создание условий для приобретения учащимся собственного опыта творческой деятельности.
Важнейшей отличительной особенностью данного курса с точки зрения содержания является включение наряду с общепринятыми для начальной школы линиями «Числа и действия над ними», «Текстовые задачи», «Величины», «Элементы геометрии», «Элементы алгебры», ещё и таких содержательных линий, как «Стохастика» и «Занимательные и нестандартные задачи». Кроме того, следует отметить, что предлагаемый курс математики содержит материалы для системной проектной деятельности и работы с жизненными (компетентностными) задачами.
Цели обучения в предлагаемом курсе математики в 3 классе, сформулированные как линии развития личности ученика средствами предмета: уметь
использовать математические представления для описания окружающего мира (предметов, процессов, явлений) в количественном и пространственном отношении;
производить вычисления для принятия решений в различных жизненных ситуациях;
читать и записывать сведения об окружающем мире на языке математики;
формировать основы рационального мышления, математической речи и аргументации;
работать в соответствии с заданными алгоритмами;
узнавать в объектах окружающего мира известные геометрические формы и работать с ними;
вести поиск информации (фактов, закономерностей, оснований для упорядочивания), преобразовать её в удобные для изучения и применения формы.
В результате освоения предметного содержания предлагаемого курса математики у учащихся предполагается формирование универсальных учебных действий (познавательных, регулятивных, коммуникативных) позволяющих достигать предметных, метапредметных и личностных результатов.
Познавательные: в предлагаемом курсе математики изучаемые определения и правила становятся основой формирования умений выделять признаки и свойства объектов. В процессе вычислений, измерений, поиска решения задач у учеников формируются основные мыслительные операции (анализа, синтеза, классификации, сравнения, аналогии и т.д.), умения различать обоснованные и необоснованные суждения, обосновывать этапы решения учебной задачи, производить анализ и преобразование информации (используя при решении самых разных математических задач простейшие предметные, знаковые, графические модели, таблицы, диаграммы, строя и преобразовывая их в соответствии с содержанием задания). Решая задачи, рассматриваемые в данном курсе, можно выстроить индивидуальные пути работы с математическим содержанием, требующие различного уровня логического мышления. Отличительной особенностью рассматриваемого курса математики является раннее появление (уже в первом классе) содержательного компонента «Элементы логики, комбинаторики, статистики и теории вероятностей», что обусловлено активной пропедевтикой этого компонента в начальной школе.
Регулятивные: математическое содержание позволяет развивать и эту группу умений. В процессе работы ребёнок учится самостоятельно определять цель своей деятельности, планировать её, самостоятельно двигаться по заданному плану, оценивать и корректировать полученный результат (такая работа задана самой структурой учебника).
Коммуникативные: в процессе изучения математики осуществляется знакомство с математическим языком, формируются речевые умения: дети учатся высказывать суждения с использованием математических терминов и понятий, формулировать вопросы и ответы в ходе выполнения задания, доказательства верности или неверности выполненного действия, обосновывают этапы решения учебной задачи.
Работая в соответствии с инструкциями к заданиям учебника, дети учатся работать в парах, выполняя заданные в учебнике проекты в малых группах. Умение достигать результата, используя общие интеллектуальные усилия и практические действия, является важнейшим умением для современного человека.
Образовательные и воспитательные задачи обучения математике решаются комплексно. В основе методического аппарата курса лежит проблемно-диалогическая технология, технология правильного типа читательской деятельности и технология оценивания достижений, позволяющие формировать у учащихся умение обучаться с высокой степенью самостоятельности. При этом в первом классе проблемная ситуация естественным образом строится на дидактической игре.
Предлагаемый учебно-методический курс также обеспечивает интеграцию в математике информационных технологий. Предполагается, что в расписании курса математики может иметь постоянное место компьютерный урок в специально оборудованном классе, где может происходить работа с цифровыми образовательными ресурсами (ЦОР) по математике, созданного на основе учебников по данному курсу (http://school-collection.edu.ru/).
Эти же ресурсы (http://school-collection.edu.ru/) могут быть использованы и на обычном уроке в обычном классе, при наличии специально оборудованного учительского места.
Деятельностный подход – основной способ получения знаний
В результате освоения предметного содержания курса математики у учащихся должны сформироваться как предметные, так и общие учебные умения, а также способы познавательной деятельности. Такая работа может эффективно осуществляться только в том случае, если ребёнок будет испытывать мотивацию к деятельности, для него будут не только ясны рассматриваемые знания и алгоритмы действий, но и представлена интересная возможность для их реализации.
Предполагается, что образовательные и воспитательные задачи обучения математике будут решаться комплексно. Учитель имеет право самостоятельного выбора технологий, методик и приёмов педагогической деятельности, однако при этом необходимо понимать, что необходимо эффективное достижение целей, обозначенных федеральным государственным образовательным стандартом начального общего образования.
Рассматриваемый курс математики предлагает решение новых образовательных задач путём использования современных образовательных технологий.
В основе методического аппарата курса лежит проблемно-диалогическая технология, технология правильного типа читательской деятельности и технология оценивания достижений, позволяющие формировать у учащихся умение обучаться с высокой степенью самостоятельности. При этом в первом классе проблемная ситуация естественным образом строится на дидактической игре.
Материалы курса организованы таким образом, чтобы педагог и дети могли осуществлять дифференцированный подход в обучении, и обладали правом выбора уровня решаемых математических задач.
В предлагаемом курсе математики представлены задачи разного уровня сложности по изучаемой теме. Это создаёт возможность построения для каждого ученика самостоятельного образовательного маршрута. Важно, чтобы его вместе планировали ученик и учитель. Именно по этой причине авторы не разделили материалы учебника на основной и дополнительный – это делают дети под руководством учителя на уроке. Учитель при этом ориентируется на требования стандартов российского образования как основы изучаемого материала.
Мы пользуемся общим для учебников Образовательной системы «Школа 2100» принципом минимакса. Согласно этому принципу учебники содержат учебные материалы, входящие в минимум содержания (базовый уровень), и задачи повышенного уровня сложности (программный и максимальный уровень), не обязательные для всех. Таким образом, ученик должен освоить минимум, но может освоить максимум.
Важнейшей отличительной особенностью данного курса с точки зрения деятельностного подхода является включение в него специальных заданий на применение существующих знаний «для себя» через дидактическую игру, проектную деятельность и работу с жизненными (компетентностными) задачами.
Алгоритм подготовки учителя к проведению урока
Проводя уроки по учебникам Образовательной системы «Школа 2100», учителя часто сталкиваются с нехваткой времени. Одна из причин этого – неумение реализовывать принцип минимакса. Рекомендуем учителю пользоваться следующим алгоритмом подготовки к уроку:
1-й шаг. На этапе подготовки к уроку следует выделить в содержании учебника обязательный программный минимум. Этот минимум должны усвоить все ученики, ведь именно эти знания и умения будут проверяться в контрольных и проверочных работах. Глубокое усвоение знаний и умений минимума обеспечивается не на одном уроке. При планировании уроков повторения, закрепления и обобщения изученного учитель должен планировать работу так, чтобы дети выполняли задания, которые нужны именно им. При этом детей в классе желательно разбивать на группы так, чтобы каждая группа выполняла свой набор заданий.
2-й шаг. В учебниках даётся несколько заданий, относящихся к уровню авторской программы. Это задания повышенного уровня сложности; и они обязательными не являются. Они могут быть предложены на заключительном этапе урока (10–15 минут), после обсуждения с детьми, при этом дети обладают правом выбора задания.
3-й шаг. В нашем учебнике к каждому уроку даётся ещё несколько заданий, которые относятся к максимальному уровню сложности. Они даны для тех детей, которым интересен процесс решения нестандартных задач, требующих самостоятельности, находчивости и упорства в поиске решения. Они также предлагаются на заключительном этапе урока по выбору детей и учителя и обязательными не являются.
4-й шаг. Кроме работы на уроке, предполагающей совместные интеллектуальные усилия, ребёнок должен учиться работать полностью самостоятельно. Для этого предназначены домашние задания. Домашнее задание состоит из двух частей: 1) общая для всех детей (инвариант); 2) задания по выбору (вариативная часть). Первая часть – это задания необходимого уровня, вторая часть – программного и максимального уровней.
Контроль за усвоением знаний
Оценка усвоения знаний и умений в предлагаемом учебно-методическом курсе математики осуществляется в процессе повторения и обобщения, выполнения текущих самостоятельных работ на этапе актуализации знаний и на этапе повторения, закрепления и обобщения изученного практически на каждом уроке, проведения этапа контроля на основе специальных тетрадей, содержащих текущие и итоговые контрольные работы.
Особенно следует отметить такой эффективный элемент контроля, связанный с использованием проблемно-диалогической технологии, как самостоятельная оценка и актуализация знаний перед началом изучения нового материала. В этом случае детям предлагается самим сформулировать необходимые для решения возникшей проблемы знания и умения и, как следствие, самим выбрать или даже придумать задания для повторения, закрепления и обобщения изученного ранее. Такая работа является одним из наиболее эффективных приёмов диагностики реальной сформированности предметных и познавательных умений у учащихся и позволяет педагогу выстроить свою деятельность с точки зрения дифференциации работы с ними.
Важную роль в проведении контроля с точки зрения выстраивания дифференцированного подхода к учащимся имеют тетради для тетради для контрольных работ. Они включают, в соответствии с принципом минимакса, не только обязательный минимум (необходимые требования), который должны усвоить все ученики, но и максимум, который они могут усвоить. При этом задания разного уровня сложности выделены в группы: задания необходимого, программного и максимального уровней, при этом ученики должны выполнить задания необходимого уровня, и могут выбирать задания других уровней как дополнительные и необязательные; акцент работ сделан на обязательном минимуме и самых важнейших положениях максимума (минимакс).
Положительные оценки и отметки за задания текущих и итоговых контрольных работ являются своеобразным зачётом по изучаемым темам. При этом срок получения зачёта не должен быть жёстко ограничен (например, ученики должны сдать все текущие темы до конца четверти). Это учит школьников планированию своих действий. Но видеть результаты своей работы школьники должны постоянно, эту роль могут играть:
- таблица требований по предмету в «Дневнике школьника». В ней ученик (с помощью учителя) выставляет свои отметки за разные задания, демонстрирующие развитие соответствующих умений;
- портфель достижений школьника – папка, в которую помещаются оригиналы или копии (бумажные, цифровые) выполненных учеником заданий, работ, содержащих не только отметку (балл), но и оценку (словесную характеристику его успехов и советов по улучшению, устранению возможных недостатков).
Накопление этих отметок и оценок показывает результаты продвижения в усвоении новых знаний и умений каждым учеником, развитие его умений действовать.
III. МЕСТО УЧЕБНОГО ПРЕДМЕТА.
Курс разработан в соответствии с базисным учебным (образовательным) планом общеобразовательных учреждений РФ.
На изучение математики в каждом классе начальной школы отводится
по 4 часа в неделю.
| Класс | Количество часов |
| 1 класс | 132 ч |
| 2 класс | 136 ч |
| 3 класс | 136 ч |
| 4 класс | 136 ч |
| Итого | 540ч |
IV. ОПИСАНИЕ ЦЕННОСТНЫХ ОРИЕНТИРОВ
Содержание, методики и дидактические основы курса математики «Учусь учиться» (технология деятельностного метода, система дидактических принципов) создают условия, механизмы и конкретные педагогические инструменты для практической реализации в ходе изучения курса расширенного набора ценностных ориентиров, важнейшими из которых являются познание – поиск истины, правды, справедливости, стремление к пониманию объективных законов мироздания и бытия, созидание – труд, направленность на создание позитивного результата и готовность брать на себя ответственность за результат, гуманизм – осознание ценности каждого человека как личности, готовность слышать и понимать других, сопереживать, при необходимости – помогать другим.
Освоение математического языка и системы математических знаний в
контексте исторического процесса их создания, понимание роли и места математики в системе наук создаёт у учащихся целостное представление о мире. Содержание курса целенаправленно формирует информационную грамотность, умение самостоятельно получать информацию из наблюдений, бесед, справочников, энциклопедий, Интернета и работать с полученной информацией.
Включение учащихся в полноценную математическую деятельность на основе метода рефлексивной самоорганизации обеспечивает поэтапное формирование у них готовности к саморазвитию и самовоспитанию.
Систематическое использование групповых форм работы, освоение
культурных норм общения и коммуникативного взаимодействия формирует навыки сотрудничества – умения работать в команде, способность следовать согласованным правилам, аргументировать свою позицию, воспринимать и учитывать разные точки зрения, находить выходы из спорных ситуаций.
Совместная деятельность помогает каждому учащемуся осознать себя частью коллектива класса, школы, страны, вырабатывает ответственность за происходящее и стремление внести свой максимальный вклад в общий результат.
Таким образом, данный курс становится площадкой, на которой у
учащихся в процессе изучения математики формируются адаптационные механизмы продуктивного действия и поведения в любых жизненных ситуациях, в том числе и тех, которые требуют изменения себя и окружающей действительности.
Ценностные ориентиры изучения предмета «Математика» в целом ограничиваются ценностью истины, однако данный курс предлагает как расширение содержания предмета (компетентностные задачи, где математическое содержание интегрировано с историческим и филологическим содержанием параллельных предметных курсов Образовательной системы «Школа 2100» ), так и совокупность методик и технологий (в том числе и проектной), позволяющих заниматься всесторонним формированием личности учащихся средствами предмета «Математика» и, как следствие, расширить набор ценностных ориентиров.
Ценность истины – это ценность научного познания как части культуры человечества, разума, понимания сущности бытия, мироздания.
Ценность человека как разумного существа, стремящегося к познанию мира и самосовершенствованию.
Ценность труда и творчества как естественного условия человеческой деятельности и жизни.
Ценность свободы как свободы выбора и предъявления человеком своих мыслей и поступков, но свободы, естественно ограниченной нормами и правилами поведения в обществе.
Ценность гражданственности – осознание человеком себя как члена общества, народа, представителя страны и государства.
Ценность патриотизма – одно из проявлений духовной зрелости человека, выражающееся в любви к России, народу, в осознанном желании служить Отечеству.
V. ЛИЧНОСТНЫЕ, МЕТАПРЕДМЕТНЫЕ И ПРЕДМЕТНЫЕ
РЕЗУЛЬТАТЫ ОСВОЕНИЯ УЧЕБНОГО ПРЕДМЕТА.
Все результаты освоения учебно-методического курса образуют целостную систему вместе с предметными средствами. Их взаимосвязь можно увидеть на схеме.
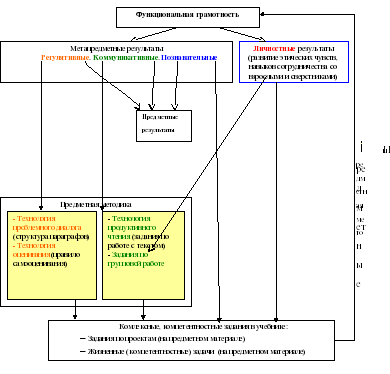
Содержание курса математики обеспечивает реализацию следующих личностных, метапредметных и предметных результатов:
Личностные результаты
Становление основ гражданской российской идентичности, уважения к своей семье и другим людям, своему Отечеству, развитие морально-этических качеств личности, адекватных полноценной математической деятельности,
Целостное восприятие окружающего мира, начальные представления об истории развития математического знания, роли математики в системе знаний.
Овладение начальными навыками адаптации в динамично изменяющемся мире на основе метода рефлексивной самоорганизации.
Принятие социальной роли «ученика», осознание личностного смысла учения и интерес к изучению математики.
Развитие самостоятельности и личной ответственности за свои поступки, способность к рефлексивной самооценке собственных действий и волевая саморегуляция.
Освоение норм общения и коммуникативного взаимодействия, навыков сотрудничества со взрослыми и сверстниками, умение находить выходы из спорных ситуаций.
Мотивация к работе на результат, как в исполнительской, так и в творческой деятельности.
Установка на здоровый образ жизни, спокойное отношение к ошибке как «рабочей» ситуации, требующей коррекции; вера в себя.
Метапредметные результаты
Умение выполнять пробное учебное действие, в случае его неуспеха грамотно фиксировать свое затруднение, анализировать ситуацию, выявлять и конструктивно устранять причины затруднения.
Освоение начальных умений проектной деятельности: постановка и сохранение целей учебной деятельности, определение наиболее эффективных способов и средств достижения результата, планирование, прогнозирование, реализация построенного проекта.
Умение контролировать и оценивать свои учебные действия на основе
выработанных критериев в соответствии с поставленной задачей и условиями ее реализации.
Опыт использования методов решения проблем творческого и поискового характера.
Освоение начальных форм познавательной и личностной рефлексии.
Способность к использованию знаково-символических средств математического языка и средств ИКТ для описания и исследования окружающего мира (представления информации, создания моделей изучаемых объектов и процессов, решения коммуникативных и познавательных задач и др.) и как базы компьютерной грамотности.
Овладение различными способами поиска (в справочной литературе, образовательных Интернет-ресурсах), сбора, обработки, анализа, организации и передачи информации в соответствии с коммуникативными и познавательными задачами, готовить свое выступление и выступать с аудио-, видео- и графическим сопровождением.
Формирование специфических для математики логических операций
(сравнение, анализ, синтез, обобщение, конкретизация, классификация, аналогия, установление причинно-следственных связей, построение рассуждений, отнесение к известным понятиям), необходимых человеку для полноценного функционирования в современном обществе; развитие логического, эвристического и алгоритмического мышления.
Овладение навыками смыслового чтения текстов.
Освоение норм коммуникативного взаимодействия в позициях «автор»,
«критик», «понимающий», «организатор», «арбитр», готовность вести диалог, признавать возможность и право каждого иметь свое мнение, способность аргументировать свою точку зрения.
Умение работать в паре и группе, договариваться о распределении функций в совместной деятельности, осуществлять взаимный контроль, адекватно оценивать собственное поведение и поведение окружающих;
стремление не допускать конфликты, а при их возникновении − готовность
конструктивно их разрешать.
Начальные представления о сущности и особенностях математического знания, истории его развития, его обобщенного характера и роли в системе знаний.
Освоение базовых предметных и межпредметных понятий (алгоритм, множество, классификация и др.), отражающих существенные связи и отношения между объектами и процессами различных предметных областей знания.
Умение работать в материальной и информационной среде начального общего образования (в том числе с учебными моделями) в соответствии с содержанием учебного предмета «математика».
Предметные результаты
Освоение опыта самостоятельной математической деятельности по получению нового знания, его преобразованию и применению для решения учебно-познавательных и учебно-практических задач.
Использование приобретенных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также оценки их количественных и пространственных отношений.
Овладение устной и письменной математической речью, основами логического, эвристического и алгоритмического мышления, пространственного воображения, счета и измерения, прикидки и оценки, наглядного представления данных и процессов (схемы, таблицы, диаграммы, графики), исполнения и построения алгоритмов.
Умение выполнять устно и письменно арифметические действия с числами, составлять числовые и буквенные выражения, находить их значения, решать текстовые задачи, простейшие уравнения и неравенства, исполнять и строить алгоритмы, составлять и исследовать простейшие формулы, распознавать, изображать и исследовать геометрические фигуры, работать с таблицами, схемами, диаграммами и графиками, множествами и цепочками, представлять, анализировать и интерпретировать данные.
Приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач.
Приобретение первоначальных представлений о компьютерной грамотности.
Приобретение первоначальных навыков работы на компьютере.
3-й классы
Личностными результатами изучения учебно-методического курса «Математика» в 3-м классе является формирование следующих умений:
В самостоятельно созданных ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, какой поступок совершить.
Средством достижения этих результатов служит учебный материал и задания учебника, нацеленные на 2-ю линию развития – умение определять свое отношение к миру.
Метапредметными результатами изучения учебно-методического курса «Математика» в 3-ем классе являются формирование следующих универсальных учебных действий.
Регулятивные УУД:
Работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки с помощью учителя.
Средством формирования этих действий служит технология проблемного диалога на этапе изучения нового материала.
Средством формирования этих действий служит технология оценивания образовательных достижений (учебных успехов).
Познавательные УУД:
Добывать новые знания: извлекать информацию, представленную в разных формах (текст, таблица, схема, иллюстрация и др.).
Средством формирования этих действий служит учебный материал и задания учебника, нацеленные на 1-ю линию развития – умение объяснять мир.
Коммуникативные УУД:
Средством формирования этих действий служит технология проблемного диалога (побуждающий и подводящий диалог).
Средством формирования этих действий служит технология продуктивного чтения.
Средством формирования этих действий служит работа в малых группах.
Предметными результатами изучения курса «Математика» в 3-м классе являются формирование следующих умений.
1-й уровень (необходимый)
Учащиеся должны уметь:
- использовать при решении учебных задач названия и последовательность чисел в пределах 1 000 (с какого числа начинается натуральный ряд чисел, как образуется каждое следующее число в этом ряду);
объяснять, как образуется каждая следующая счётная единица;
использовать при решении учебных задач единицы измерения длины (мм, см, дм, м, км), объёма (литр, см3, дм3, м3), массы (кг, центнер), площади (см2, дм2, м2), времени (секунда, минута, час, сутки, неделя, месяц, год, век) и соотношение между единицами измерения каждой из величин;
использовать при решении учебных задач формулы площади и периметра прямоугольника (квадрата);
пользоваться для объяснения и обоснования своих действий изученной математической терминологией;
читать, записывать и сравнивать числа в пределах 1 000;
представлять любое трёхзначное число в виде суммы разрядных слагаемых;
выполнять устно умножение и деление чисел в пределах 100 (в том числе и деление с остатком);
выполнять умножение и деление с 0; 1; 10; 100;
осознанно следовать алгоритмам устных вычислений при сложении, вычитании, умножении и делении трёхзначных чисел, сводимых к вычислениям в пределах 100, и алгоритмам письменных вычислений при сложении, вычитании, умножении и делении чисел в остальных случаях;
осознанно следовать алгоритмам проверки вычислений;
использовать при вычислениях и решениях различных задач распределительное свойство умножения и деления относительно суммы (умножение и деление суммы на число), сочетательное свойство умножения для рационализации вычислений;
читать числовые и буквенные выражения, содержащие не более двух действий с использованием названий компонентов;
решать задачи в 1–2 действия на все арифметические действия арифметическим способом (с опорой на схемы, таблицы, краткие записи и другие модели);
находить значения выражений в 2–4 действия;
использовать знание соответствующих формул площади и периметра прямоугольника (квадрата) при решении различных задач;
использовать знание зависимости между компонентами и результатами действий при решении уравнений вида а ± х = b; а ∙ х = b; а : х = b;
строить на клетчатой бумаге прямоугольник и квадрат по заданным длинам сторон;
сравнивать величины по их числовым значениям; выражать данные величины в изученных единицах измерения;
определять время по часам с точностью до минуты;
сравнивать и упорядочивать объекты по разным признакам: длине, массе, объёму;
устанавливать зависимость между величинами, характеризующими процессы: движения (пройденный путь, время, скорость), купли – продажи (количество товара, его цена и стоимость).
2-й уровень (программный)
Учащиеся должны уметь:
использовать при решении различных задач знание формулы объёма прямоугольного параллелепипеда (куба);
использовать при решении различных задач знание формулы пути;
использовать при решении различных задач знание о количестве, названиях и последовательности дней недели, месяцев в году;
находить долю от числа, число по доле;
решать задачи в 2–3 действия на все арифметические действия арифметическим способом (с опорой на схемы, таблицы, краткие записи и другие модели);
а ± х b; а ∙ х b.
- использовать знание зависимости между компонентами и результатами действий при решении уравнений вида: х ± а = с ± b; а – х = с ± b; х ± a = с ∙ b; а – х = с : b; х : а = с±b;
- выделять из множества треугольников прямоугольный и тупоугольный, равнобедренный и равносторонний треугольники;
строить окружность по заданному радиусу;
выделять из множества геометрических фигур плоские и объёмные фигуры;
узнавать и называть объёмные фигуры: параллелепипед, шар, конус, пирамиду, цилиндр;
выделять из множества параллелепипедов куб;
решать арифметические ребусы и числовые головоломки, содержащие четыре арифметических действия (сложение, вычитание, умножение, деление);
устанавливать принадлежность или непринадлежность множеству данных элементов;
различать истинные и ложные высказывания с кванторами общности и существования;
читать информацию, заданную с помощью столбчатых, линейных диаграмм, таблиц, графов;
строить несложные линейные и столбчатые диаграммы по заданной в таблице информации;
решать удобным для себя способом (в том числе и с помощью таблиц и графов) комбинаторные задачи: на перестановку из трёх элементов, правило произведения, установление числа пар на множестве из 3–5 элементов;
решать удобным для себя способом (в том числе и с помощью таблиц и графов) логические задачи, содержащие не более трёх высказываний;
выписывать множество всевозможных результатов (исходов) простейших случайных экспериментов;
- правильно употреблять термины «чаще», «реже», «случайно», «возможно», «невозможно» при формулировании различных высказываний;
составлять алгоритмы решения простейших задач на переливания;
составлять алгоритм поиска одной фальшивой монеты на чашечных весах без гирь (при количестве монет не более девяти);
устанавливать, является ли данная кривая уникурсальной, и обводить её.
VI. СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО ПРЕДМЕТА
В предлагаемом курсе математики выделяются несколько содержательных линий.
1. Числа и операции над ними. Понятие натурального числа является одним из центральных понятий начального курса математики. Формирование этого понятия осуществляется практически в течение всех лет обучения. Раскрывается это понятие на конкретной основе в результате практического оперирования конечными предметными множествами; в процессе счёта предметов, в процессе измерения величин. В результате раскрываются три подхода к построению математической модели понятия «число»: количественное число, порядковое число, число как мера величины.
В тесной связи с понятием числа формируется понятие о десятичной системе счисления. Раскрывается оно постепенно, в ходе изучения нумерации и арифметических операций над натуральными числами. При изучении нумерации деятельность учащихся направляется на осознание позиционного принципа десятичной системы счисления и на соотношение разрядных единиц.
Важное место в начальном курсе математики занимает понятие арифметической операции. Смысл каждой арифметической операции раскрывается на конкретной основе в процессе выполнения операций над группами предметов, вводится соответствующая символика и терминология. При изучении каждой операции рассматривается возможность её обращения.
Важное значение при изучении операций над числами имеет усвоение табличных случаев сложения и умножения. Чтобы обеспечить прочное овладение ими, необходимо, во-первых, своевременно создать у детей установку на запоминание, во-вторых, практически на каждом уроке организовать работу тренировочного характера. Задания, предлагаемые детям, должны отличаться разнообразием и способствовать включению в работу всех детей класса. Необходимо использовать приёмы, формы работы, способствующие поддержанию интереса детей, а также различные средства обратной связи.
В предлагаемом курсе изучаются некоторые основные законы математики и их практические приложения:
коммутативный закон сложения и умножения;
ассоциативный закон сложения и умножения;
дистрибутивный закон умножения относительно сложения.
Все эти законы изучаются в связи с арифметическими операциями, рассматриваются на конкретном материале и направлены, главным образом, на формирование вычислительных навыков учащихся, на умение применять рациональные приёмы вычислений.
Следует отметить, что наиболее важное значение в курсе математики начальных классов имеют не только сами законы, но и их практические приложения. Главное – научить детей применять эти законы при выполнении устных и письменных вычислений, в ходе решения задач, при выполнении измерений. Для усвоения устных вычислительных приемов используются различные предметные и знаковые модели.
В соответствии с требованиями стандарта, при изучении математики в начальных классах у детей необходимо сформировать прочные осознанные вычислительные навыки, в некоторых случаях они должны быть доведены до автоматизма.
Значение вычислительных навыков состоит не только в том, что без них учащиеся не в состоянии овладеть содержанием всех последующих разделов школьного курса математики. Без них они не в состоянии овладеть содержанием и таких учебных дисциплин, как, например, физика и химия, в которых систематически используются различные вычисления.
Наряду с устными приёмами вычислений в программе большое значение уделяется обучению детей письменным приёмам вычислений. При ознакомлении с письменными приёмами важное значение придается алгоритмизации.
В программу курса введены понятия «целое» и «часть». Учащиеся усваивают разбиение на части множеств и величин, взаимосвязь между целым и частью. Это позволяет им осознать взаимосвязь между операциями сложения и вычитания, между компонентами и результатом действия, что, в свою очередь, станет основой формирования вычислительных навыков, обучения решению текстовых задач и уравнений.
Современный уровень развития науки и техники требует включения в обучение школьников знакомство с моделями и основами моделирования, а также формирования у них навыков алгоритмического мышления. Без применения моделей и моделирования невозможно эффективное изучение исследуемых объектов в различных сферах человеческой деятельности, а правильное и чёткое выполнение определённой последовательности действий требует от специалистов многих профессий владения навыками алгоритмического мышления. Разработка и использование станков-автоматов, компьютеров, экспертных систем, долгосрочных прогнозов – вот неполный перечень применения знаний основ моделирования и алгоритмизации. Поэтому формирование у младших школьников алгоритмического мышления, умений построения простейших алгоритмов и моделей – одна из важнейших задач современной общеобразовательной школы.
Обучение школьников умению «видеть» алгоритмы и осознавать алгоритмическую сущность тех действий, которые они выполняют, начинается с простейших алгоритмов, доступных и понятных им (алгоритмы пользования бытовыми приборами, приготовления различных блюд, переход улицы и т.п.). В начальном курсе математики алгоритмы представлены в виде правил, последовательности действий и т.п. Например, при изучении арифметических операций над многозначными числами учащиеся пользуются правилами сложения, умножения, вычитания и деления многозначных чисел, при изучении дробей – правилами сравнения дробей и т.д. Программа позволяет обеспечить на всех этапах обучения высокую алгоритмическую подготовку учащихся.
2. Величины и их измерение. Величина также является одним из основных понятий начального курса математики. В процессе изучения математики у детей необходимо сформировать представление о каждой из изучаемых величин (длина, масса, время, площадь, объем и др.) как о некотором свойстве предметов и явлений окружающей нас жизни, а также умение выполнять измерение величин.
Формирование представления о каждых из включённых в программу величин и способах её измерения имеет свои особенности. Однако можно выделить общие положения, общие этапы, которые имеют место при изучении каждой из величин в начальных классах:
выясняются и уточняются представления детей о данной величине (жизненный опыт ребёнка);
проводится сравнение однородных величин (визуально, с помощью ощущений, непосредственным сравнением с использованием различных условных мерок и без них);
проводится знакомство с единицей измерения данной величины и с измерительным прибором;
формируются измерительные умения и навыки;
выполняется сложение и вычитание значений однородных величин, выраженных в единицах одного наименования (в ходе решения задач);
проводится знакомство с новыми единицами измерения величины;
выполняется сложение и вычитание значений величины, выраженных в единицах двух наименований;
выполняется умножение и деление величины на отвлечённое число. При изучении величин имеются особенности и в организации деятельности учащихся.
Важное место занимают средства наглядности как демонстрационные, так и индивидуальные, сочетание различных форм обучения на уроке (коллективных, групповых и индивидуальных).
Немаловажное значение имеют удачно выбранные методы обучения, среди которых группа практических методов и практических работ занимает особое место. Широкие возможности создаются здесь и для использования проблемных ситуаций.
В ходе формирования у учащихся представления о величинах создаются возможности для пропедевтики понятия функциональной зависимости. Основной упор при формировании представления о функциональной зависимости делается на раскрытие закономерностей того, как изменение одной величины влияет на изменение другой, связанной с ней величины. Эта взаимосвязь может быть представлена в различных видах: рисунком, графиком, схемой, таблицей, диаграммой, формулой, правилом.
3. Текстовые задачи. В начальном курсе математики особое место отводится простым (опорным) задачам. Умение решать такие задачи − фундамент, на котором строится работа с более сложными задачами.
В ходе решения опорных задач учащиеся усваивают смысл арифметических действий, связь между компонентами и результатами действий, зависимость между величинами и другие вопросы.
Работа с текстовыми задачами является очень важным и вместе с тем весьма трудным для детей разделом математического образования. Процесс решения задачи является многоэтапным: он включает в себя перевод словесного, текста на язык математики (построение математической модели), математическое решение, а затем анализ полученных результатов. Работе с текстовыми задачами следует уделить достаточно много времени, обращая внимание детей на поиск и сравнение различных способов решения задачи, построение математических моделей, грамотность изложения собственных рассуждений при решении задач.
Учащихся следует знакомить с различными методами решения текстовых задач: арифметическим, алгебраическим, геометрическим, логическим и практическим; с различными видами математических моделей, лежащих в основе каждого метода; а также с различными способами решения в рамках выбранного метода.
Решение текстовых задач даёт богатый материал для развития и воспитания учащихся.
Краткие записи условий текстовых задач – примеры моделей, используемых в начальном курсе математики. Метод математического моделирования позволяет научить школьников: а) анализу (на этапе восприятия задачи и выбора пути реализации решения); б) установлению взаимосвязей между объектами задачи, построению наиболее целесообразной схемы решения; в) интерпретации полученного решения для исходной задачи; г) составлению задач по готовым моделям и др.
4. Элементы геометрии. Изучение геометрического материала служит двум основным целям: формированию у учащихся пространственных представлений и ознакомлению с геометрическими величинами (длиной, площадью, объёмом).
Наряду с этим одной из важных целей работы с геометрическим материалом является использование его в качестве одного из средств наглядности при рассмотрении некоторых арифметических фактов. Кроме этого, предполагается установление связи между арифметикой и геометрией на начальном этапе обучения математике для расширения сферы применения приобретённых детьми арифметических знаний, умений и навыков.
Геометрический материал изучается в течение всех лет обучения в начальных классах, начиная с первых уроков.
В изучении геометрического материала просматриваются два направления:
формирование представлений о геометрических фигурах;
формирование некоторых практических умений, связанных с построением геометрических фигур и измерениями.
Геометрический материал распределён по годам обучения и по урокам так, что при изучении он включается отдельными частями, которые определены программой и соответствующим учебником.
Преимущественно уроки математики следует строить так, чтобы главную часть их составлял арифметический материал, а геометрический материал входил бы составной частью. Это создает большие возможности для осуществления связи геометрических и других знаний, а также позволяет вносить определённое разнообразие в учебную деятельность на уроках математики, что очень важно для детей этого возраста, а кроме того, содействует повышению эффективности обучения.
Программа предусматривает формирование у школьников представлений о различных геометрических фигурах и их свойствах: точке, линиях (кривой, прямой, ломаной), отрезке, многоугольниках различных видов и их элементах, окружности, круге и др.
Учитель должен стремиться к усвоению детьми названий изучаемых геометрических фигур и их основных свойств, а также сформировать умение выполнять их построение на клетчатой бумаге.
Отмечая особенности изучения геометрических фигур, следует обратить внимание на то обстоятельство, что свойства всех изучаемых фигур выявляются экспериментальным путём в ходе выполнения соответствующих упражнений.
Важную роль при этом играет выбор методов обучения. Значительное место при изучении геометрических фигур и их свойств должна занимать группа практических методов, и особенно практические работы.
Систематически должны проводиться такие виды работ, как изготовление геометрических фигур из бумаги, палочек, пластилина, их вырезание, моделирование и др. При этом важно учить детей различать существенные и несущественные признаки фигур. Большое внимание при этом следует уделить использованию приёма сопоставления и противопоставления геометрических фигур.
Предложенные в учебнике упражнения, в ходе выполнения которых происходит формирование представлений о геометрических фигурах, можно охарактеризовать как задания:
в которых геометрические фигуры используются как объекты для пересчитывания;
на классификацию фигур;
на выявление геометрической формы реальных объектов или их частей;
на построение геометрических фигур;
на разбиение фигуры на части и составление её из других фигур;
на формирование умения читать геометрические чертежи;
вычислительного характера (сумма длин сторон многоугольника и др.).
Знакомству с геометрическими фигурами и их свойствами способствуют и простейшие задачи на построение. В ходе их выполнения необходимо учить детей пользоваться чертёжными инструментами, формировать у них чертёжные навыки. Здесь надо предъявлять к учащимся требования не меньшие, чем при формировании навыков письма и счёта.
Элементы алгебры. В курсе математики для начальных классов формируются некоторые понятия, связанные с алгеброй. Это понятия выражения, равенства, неравенства (числового и буквенного), уравнения и формулы. Суть этих понятий раскрывается на конкретной основе, изучение их увязывается с изучением арифметического материала. У учащихся формируются умения правильно пользоваться математической терминологией и символикой.
Элементы стохастики. Наша жизнь состоит из явлений стохастического характера. Поэтому современному человеку необходимо иметь представление об основных методах анализа данных и вероятностных закономерностях, играющих важную роль в науке, технике и экономике. В этой связи элементы комбинаторики, теории вероятностей и математической статистики входят в школьный курс математики в виде одной из сквозных содержательно-методических линий, которая даёт возможность накопить определённый запас представлений о статистическом характере окружающих явлений и об их свойствах.
В начальной школе стохастика представлена в виде элементов комбинаторики, теории графов, наглядной и описательной статистики, начальных понятий теории вероятностей. С их изучением тесно связано формирование у младших школьников отдельных комбинаторных способностей, вероятностных понятий («чаще», «реже», «невозможно», «возможно» и др.), начал статистической культуры.
Базу для решения вероятностных задач создают комбинаторные задачи. Использование комбинаторных задач позволяет расширить знания детей о задаче, познакомить их с новым способом решения задач; формирует умение принимать решения, оптимальные в данном случае; развивает элементы творческой деятельности.
Комбинаторные задачи, предлагаемые в начальных классах, как правило, носят практическую направленность и основаны на реальном сюжете. Это вызвано в первую очередь психологическими особенностями младших школьников, их слабыми способностями к абстрактному мышлению. В этой связи система упражнений строится таким образом, чтобы обеспечить постепенный переход от манипуляции с предметами к действиям в уме.
Такое содержание учебного материала способствует развитию внутрипредметных и межпредметных связей (в частности, математики и естествознания), позволяет осуществлять прикладную направленность курса, раскрывает роль современной математики в познании окружающей действительности, формирует мировоззрение. Человеку, не понявшему вероятностных идей в раннем детстве, в более позднем возрасте они даются нелегко, так как многое в теории вероятностей кажется противоречащим жизненному опыту, а с возрастом опыт набирается и приобретает статус безусловности. Поэтому очень важно формировать стохастическую культуру, развивать вероятностную интуицию и комбинаторные способности детей в раннем возрасте.
7. Нестандартные и занимательные задачи. В настоящее время одной из тенденций улучшения качества образования становится ориентация на развитие творческого потенциала личности ученика на всех этапах обучения в школе, на развитие его творческого мышления, на умение использовать эвристические методы в процессе открытия нового и поиска выхода из различных нестандартных ситуаций и положений.
Математика – это орудие для размышления, в её арсенале имеется большое количество задач, которые на протяжении тысячелетий способствовали формированию мышления людей, умению решать нестандартные задачи, с честью выходить из затруднительных положений.
К тому же воспитание интереса младших школьников к математике, развитие их математических способностей невозможно без использования в учебном процессе задач на сообразительность, задач-шуток, математических фокусов, числовых головоломок, арифметических ребусов и лабиринтов, дидактических игр, стихов, задач-сказок, загадок и т.п.
Начиная с первого класса, при решении такого рода задач, как и других, предлагаемых в курсе математики, школьников необходимо учить применять теоретические сведения для обоснования рассуждений в ходе их решения; правильно проводить логические рассуждения; формулировать утверждение, обратное данному; проводить несложные классификации, приводить примеры и контрпримеры.
В основу построения программы положен принцип построения содержания предмета «по спирали». Многие математические понятия и методы не могут быть восприняты учащимися сразу. Необходим долгий и трудный путь к их осознанному пониманию. Процесс формирования математических понятий должен проходить в своём развитии несколько ступеней, стадий, уровней.
Сложность содержания материала, недостаточная подготовленность учащихся к его осмыслению приводят к необходимости растягивания процесса его изучения во времени и отказа от линейного пути его изучения.
Построение содержания предмета «по спирали» позволяет к концу обучения в школе постепенно перейти от наглядного к формально-логическому изложению, от наблюдений и экспериментов – к точным формулировкам и доказательствам.
Материал излагается так, что при дальнейшем изучении происходит развитие имеющихся знаний учащегося, их перевод на более высокий уровень усвоения, но не происходит отрицания того, что учащийся знает.
Виды и формы контроля
В курсе математики в 3 классе предусмотрен текущий, тематический и итоговый контроль. Для текущего контроля используются самостоятельные работы на печатной основе, которые проводятся по пройденному материалу приблизительно раз в неделю.
Самостоятельные работы носят обучающий характер. При проведении самостоятельных работ ставится, прежде всего, цель - выявить уровень математической подготовки детей и своевременно устранить имеющиеся пробелы знаний. Уровень трудности работ, как правило, высок. Работы рассчитываются на 10-15 минут. Оценка за самостоятельные работы ставится после того, как проведена работа над ошибками. Оценивается не столько то, что ребёнок успел сделать во время урока, а то, как в итоге он поработал над материалом. В самостоятельных работах принципиально важно качество работы над собой и оценивается только успех.
Основная функция контрольных работ – контроль знаний. Результаты контрольной работы не исправляются. На контрольные работы отводится от 30 до 45 ми нут. Проводятся они примерно 2-3 раза в четверть.
В конце года дети сначала пишут переводную работу, определяющую способность к продолжению обучения в следующем классе в соответствии с государственным стандартом знаний, а затем – итоговую контрольную работу, выявляющую глубину и прочность усвоения программного материала.
Время выполнения итоговой работы может быть увеличено до двух учебных часов.
3-й класс
Числа и арифметические действия с ними
Счет тысячами. Разряды и классы: класс единиц, класс тысяч, класс миллионов и т.д. Нумерация, сравнение, сложение и вычитание многозначных чисел (в пределах 1 000 000 000 000). Представление натурального числа в виде суммы разрядных слагаемых.
Умножение и деление чисел на 10, 100, 1000 и т.д. Письменное умножение и деление (без остатка) круглых чисел.
Умножение многозначного числа на однозначное. Запись умножения «в столбик».
Деление многозначного числа на однозначное. Запись деления «углом».
Умножение на двузначное и трехзначное число. Общий случай умножения многозначных чисел.
Проверка правильности выполнения действий с многозначными числа-
ми: алгоритм, обратное действие, вычисление на калькуляторе.
Устное сложение, вычитание, умножение и деление многозначных чисел в случаях, сводимых к действиям в пределах 100.
Упрощение вычислений с многозначными числами на основе свойств
арифметических действий.
Построение и использование алгоритмов изученных случаев устных и
письменных действий с многозначными числами.
Работа с текстовыми задачами
Анализ задачи, построение графических моделей и таблиц, планирование и реализация решения. Поиск разных способов решения.
Составные задачи в 2−4 действия с натуральными числами на смысл действий сложения, вычитания, умножения и деления, разностное и кратное сравнение чисел.
Задачи, содержащие зависимость между величинами вида a = b × c:
путь − скорость − время (задачи на движение), объем выполненной работы −
производительность труда − время (задачи на работу), стоимость – цена товара − количество товара (задачи на стоимость) и др.
Классификация простых задач изученных типов. Общий способ анализа и решения составной задачи.
Задачи на определение начала, конца и продолжительности события.
Задачи на нахождение чисел по их сумме и разности.
Задачи на вычисление площадей фигур, составленных из прямоугольников и квадратов.
Сложение и вычитание изученных величин при решении задач.
Геометрические фигуры и величины
Преобразование фигур на плоскости. Симметрия фигур относительно пря-
мой. Фигуры, имеющие ось симметрии. Построение симметричных фигур на
клетчатой бумаге.
Прямоугольный параллелепипед, куб, их вершины, ребра и грани. Построение развертки и модели куба и прямоугольного параллелепипеда.
Единицы длины: миллиметр, сантиметр, дециметр, метр, километр,
соотношения между ними.
Преобразование геометрических величин, сравнение их значений, сложение, вычитание, умножение и деление на натуральное число.
Величины и зависимости между ними
Наблюдение зависимостей между величинами и их фиксирование с помощью таблиц.
Измерение времени. Единицы измерения времени: год, месяц, неделя, сутки, час, минута, секунда. Определение времени по часам. Название месяцев и дней недели. Календарь. Соотношение между единицами измерения времени.
Единицы массы: грамм, килограмм, центнер, тонна, соотношения между ними.
Преобразование, сравнение, сложение и вычитание однородных величин.
Переменная. Выражение с переменной. Значение выражения с переменной.
Формула. Формулы площади и периметра прямоугольника: S = a ∙ b,
P = (a + b) × 2. Формулы площади и периметра квадрата: S = a ∙ а, P = 4 ∙ a.
Формула объема прямоугольного параллелепипеда: V = a × b × c. Формула
объема куба: V = a × а × а.
Формула пути s = v × t и ее аналоги: формула стоимости С = а × х, формула работы А = w × t и др., их обобщенная запись с помощью формулы
a = b × c.
Наблюдение зависимостей между величинами, их фиксирование с помощью таблиц и формул. Построение таблиц по формулам зависимостей и формул зависимостей по таблицам.
Алгебраические представления
Формула деления с остатком: a = b × c + r, r
Уравнение. Корень уравнения. Множество корней уравнения. Со-
ставные уравнения, сводящиеся к цепочке простых (вида а + х = b, а – х = b,
x – a = b, а × х = b, а : х = b, x : a = b). Комментирование решения уравнений
по компонентам действий.
Математический язык и элементы логики
Знакомство с символической записью многозначных чисел, обозначением их разрядов и классов, с языком уравнений, множеств, переменных и формул, изображением пространственных фигур.
Высказывание. Верные и неверные высказывания. Определение истинности и ложности высказываний. Построение простейших высказываний с помощью логических связок и слов «верно/неверно, что ...», «не», «если ...,
то ...», «каждый», «все», «найдется», «всегда», «иногда».
Множество. Элемент множества. Знаки Î и Ï. Задание множества
перечислением его элементов и свойством.
Пустое множество и его обозначение: Æ. Равные множества. Диаграмма Эйлера−Венна.
Подмножество. Знаки U и ∩. Пересечение множеств. Знак. Свойства пересечения множеств. Объединение множеств. Знак. Свойства объединения множеств.
Переменная. Формула.
Работа с информацией и анализ данных
Использование таблиц для представления и систематизации данных.
Интерпретация данных таблицы.
Классификация элементов множества по свойству. Упорядочение и систематизация информации в справочной литературе.
Решение задач на упорядоченный перебор вариантов с помощью таблиц и дерева возможностей
Выполнение проектных работ по темам: «Из истории натуральных чисел», «Из истории календаря». Планирование поиска и организации информации Поиск информации в справочниках, энциклопедиях, Интернет-ресурсах. Оформление и представление результатов выполнения проектных работ.
Творческие работы учащихся по теме: «Красота и симметрия в жизни».
Обобщение и систематизация знаний, изученных в 3 классе.
VI. ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ С УКАЗАНИЕМ ОСНОВНЫХ ВИДОВ УЧЕБНОЙ ДЕЯЕЛЬНОСТИ
| № п/п | Тема урока | Виды учебной деятельности | Кол-во часов |
| 1 | 1 часть. Множество и его элементы. Число элементов множества | Составлять множества, заданные перечислением и общим свойством элементов. Использовать знак принадлежности элемента множеству. Обозначать множества, определять принадлежность элемента множеству. Использовать знак пустого множества | 1 |
| 2 | Способы задания множества | Составлять множества, заданные перечислением и общим свойством элементов. Учиться, совместно с учителем, обнаруживать и определять учебную проблему. | 1 |
| 3 | Равные множества. Пустое множество. Знак Ø. | Использовать знак принадлежности элемента множеству. Определять равенство и неравенство множеств. Составлять множества, заданные перечислением и общим свойством элементов. Обозначать множества, определять принадлежность элемента множеству. | 1 |
| 4 | Диаграммы Эйлера- Венна. Знаки Є и Є | Наглядно отображать множества с помощью диаграмм Эйлера – Венна. Использовать знак принадлежности элемента множеству. Обозначать множества, определять принадлежность элемента множеству. | 1 |
| 5 | Диаграммы Эйлера- Венна. Знаки Є и Є. (С-1, 2) | Наглядно изображать множества с помощью диаграмм Эйлера – Венна. Уметь работать в группе, сотрудничать в совместном решении проблемы (задачи). | 1 |
| 6 | Подмножество. | Устанавливать, является ли одно множество подмножеством другого. Записывать результат с помощью знаков. Изображать множество и его подмножество на диаграмме Венна. | 1 |
| 7 | Задачи на приведение к 1. | Разбивать множества на части (классификация). Использовать язык множеств для решения логических задач. Строить общий способ решения задач на приведение к единице, применять его для решения задач. | 1 |
| 8 | Разбиение множества на части по свойствам (классификация). | Сравнивать объекты, группировать по заданному признаку. Учиться оценивать успешность выполнения работы, исходя из имеющихся критериев. | 1 |
| 9 | Подмножество. Задачи на приведение к 1. (С-3) | Использовать язык множеств для решения логических задач. Строить общий способ решения задач на приведение к единице, применять его при решении задач | 1 |
| 10 | Пересечение множеств. Свойства операции пересечения множеств. | Находить объединение и пересечение множеств. Записывать результат с помощью знаков. Изображать объединение и пересечение множеств на диаграмме Венна. Моделировать пересечение геометрических фигур с помощью предметных моделей. | 1 |
| 11 | Пересечение множеств и его свойства (С-4) | Использовать язык множеств для решения логических задач. Строить общий способ решения задач на приведение к единице, применять его для решения задач. Изображать объединение и пересечение множеств на диаграмме Венна. Моделировать пересечение геометрических фигур с помощью предметных моделей. | 1 |
| 12 | Задачи на приведение к 1 (второй тип) | Выполнять умножение и деление двузначного числа на однозначное; Решать задачи с пропорциональными величинами. Составлять план решения проблемы (задачи) совместно с учителем. | 1 |
| 13 | Объединение множеств. Знак U | Исследовать свойства объединения и пересечения множеств с помощью диаграмм Эйлера – Венна. Устанавливать их анализ с переместительным и сочетательным свойствами сложения и умножения чисел. | 1 |
| 14 | Запись умножения в столбик | Закреплять вычислительные навыки, повторить таблицу умножения, нахождение площади фигур. | 1 |
| 15 | Объединения множеств и его свойства. Задачи на приведение к 1 (второй тип) (С-5) | Находить объединение и пересечение множеств. Записывать результат с помощью знаков. Изображать объединение и пересечение множеств на диаграмме Венна. Моделировать пересечение геометрических фигур с помощью предметных моделей. | 1 |
| 16 | Сложение и вычитание множеств. | Решать вычислительные примеры, на порядок действий, уравнения изученных типов. Находить значения буквенных выражений при данных значениях букв. Представлять данные в таблице, выявлять. | 1 |
| 17 | Множества и операции над ними. Задачи на приведение к 1. | Находить объединение множеств, пересечение множеств; выполнять операции умножения и деления двузначного числа на однозначное; решать задачи с пропорциональными величинами | 1 |
| 18 | Контрольная работа по теме «Множества». | Применять изученные способы действий для решения задач в типовых и поисковых ситуациях. Контролировать правильность и полноту выполнения изученных способов действий. | 1 |
| 19 | Работа над ошибками по теме: «Множества». Выполнение проектных работ по теме «Как люди научились считать». | Планировать поиск и организацию информации. Искать информацию в учебнике, справочниках, энциклопедиях и др. Оформлять и представлять результаты выполнения проектных работ. Работать в группах: распределять роли между членами группы, планировать работу, распределять виды работы, определять. | 1 |
| 20 | Обобщение и систематизация изученного материала. История развития понятия числа. | Перерабатывать полученную информацию: сравнивать и группировать факты и явления; определять причины явлений, событий. Донести свою позицию до других: высказывать свою точку зрения и пытаться её обосновать, приводя аргументы. Самостоятельно определять и высказывать самые простые, общие для всех людей правила поведения при совместной работе и сотрудничестве (этические нормы). | 1 |
| 21 | Нумерация натуральных чисел. Многозначные числа. | Читать и записывать натуральные числа в пределах триллиона (12 разрядов). Определять и называть цифру каждого разряда. Устанавливать правила поразрядного сравнения натуральных чисел. | 1 |
| 22 | Сравнение многозначных чисел. | Читать и записывать многозначные числа, сравнивать их, знать их десятичный состав. Самостоятельно формулировать цели урока после предварительного обсуждения. | 1 |
| 23 | Нумерация и сравнение многозначных чисел. (С-6) | Устанавливать правила поразрядного сравнения натуральных чисел. Применять их для сравнения многозначных чисел. Сравнивать выражения на основе взаимосвязи между компонентами и результатами действий. | 1 |
| 24 | Сравнение, сложение и вычитание многозначных чисел. | Сравнивать числа по разрядам. Группировать числа по заданному или самостоятельно установленному правилу. | 1 |
| 25 | Сравнение, сложение и вычитание многозначных чисел. (С-7) | Складывать и вычитать многозначные числа. Решать примеры, задачи и уравнения на сложение и вычитание многозначных чисел. Записывать многозначные числа римскими цифрами. | 1 |
| 26 | Сложение и вычитание многозначных чисел. | Решать вычислительные примеры, уравнения, простые и составные задачи изученных типов. Составлять числовые и буквенные выражения к задачам и задачи по заданным выражениям. Выполнять задания поискового и творческого характера. | 1 |
| 27 | Сложение и вычитание многозначных чисел. (С-8) | Применять изученные способы действий для решения задач в типовых и поисковых ситуациях. | 1 |
| 28 | Контрольная работа. «Сравнение, сложение и вычитание многозначных чисел» | Контролировать правильность и полноту выполнения изученных способов действий. | 1 |
| 29 | Работа над ошибками, «Сравнение, сложение и вычитание многозначных чисел». | Выявлять причину ошибки и корректировать ее, оценивать свою работу. | 1 |
| 30 | Умножение на 10, 100, 1000. | Строить и применять алгоритмы умножения и деления на 10, 100… умножение круглых чисел. Обосновывать правильность своих действий с помощью построенных алгоритмов. Осуществлять самоконтроль | 1 |
| 31 | Умножение круглых чисел. (С-9) | Повторение правил умножения круглых чисел, закрепление знаний учащихся о многозначных числах. | 1 |
| 32 | Контрольная работа за 1 четверть «Множества», «Сложение и вычитание многозначных чисел». | Контролировать правильность и полноту выполнения изученных способов действий. | 1 |
| 33 | Работа над ошибками. Деление на 10, 100, 1000. | Строить и применять алгоритмы умножения и деления на 10, 100… деление круглых чисел. Обосновывать правильность своих действий с помощью построенных алгоритмов. Осуществлять самоконтроль | 1 |
| 34 | Деление круглых чисел. (С-10) | Повторение правил деления круглых чисел, закрепление знаний нумерации многозначных чисел, отработка навыков устных и письменных вычислений. | 1 |
| 35 | Единицы длины | Уточнять соотношение между единицами длины. Выводить общее правило перехода к большим меркам и перехода к меньшим меркам. Применять это правило для преобразования единиц длины. Сравнивать и складывать, вычитать однородные величины.
| 1 |
| 36 | Единицы длины. Практическая работа «Измерение отрезков и их построение». (С-11) | Закрепление знаний учащихся о единицах измерения длины, развитие умения переводить величины из одних единиц измерения в другие. | 1 |
| 37 | Единицы массы. Грамм. Тонна. Центнер. (С-12) | Уточнять соотношение между единицами массы. Выводить общее правило перехода к большим меркам и перехода к меньшим меркам. Применять это правило для преобразования единиц массы. Сравнивать и складывать, вычитать однородные величины. | 1 |
| 38 | Игра-путешествие. ИКС-педиция к Математическому полюсу. | Применять изученные способы действий для решения задач в типовых и поисковых ситуациях. | 1 |
| 39 | Контрольная работа по теме «Умножение и деление круглых чисел. Единицы измерения». | Контролировать правильность и полноту выполнения изученных способов действий. | 1 |
| 40 | Работа над ошибками. Умножение многозначного числа на однозначное. | Выявлять причину ошибки и корректировать ее, оценивать свою работу. | 1 |
| 41 | Умножение многозначного числа на однозначное. Запись умножения в «столбик» | Строить и применять алгоритмы умножения многозначного числа на однозначное число. | 1 |
| 42 | Умножение многозначных круглых чисел. | Анализировать и интерпретировать данные таблицы. Решать задачи на нахождение периметра треугольника, площади фигур, составленных из прямоугольников. | 1 |
| 43 | Решение задач по сумме и разности | Строить общий способ решения задач «по сумме и разности». Анализировать и интерпретировать данные таблицы. | 1 |
| 44 | Умножение многозначных круглых чисел. Решение задач по сумме и разности. | Решать задачи на нахождение периметра треугольника, площади фигур, составленных из прямоугольников. | 1 |
| 45 | Деление многозначного числа на однозначное и случаи, сводящиеся к делению на однозначное число. Запись деления «углом». | Строить и применять алгоритмы деления многозначного числа на однозначное число. Анализировать и интерпретировать данные таблицы. Решать задачи на нахождение периметра треугольника, площади фигур, составленных из прямоугольников. Записывать деление уголком. | 1 |
| 46 | Деление многозначного числа на однозначное. | Записывать деление уголком. Строить и применять алгоритмы деления многозначного числа на однозначное число. | 1 |
| 47 | Деление многозначного числа с нулём посередине на однозначное число. (С-13) | Составлять, читать и записывать числовые и буквенные выражения, содержащие все 4 арифметических действия. Находить значение выражения. Записывать деление уголком. Строить и применять алгоритмы деления многозначного числа на однозначное число. | 1 |
| 48 | Деление многозначного числа с нулём на конце на однозначное число. | Знакомство учащихся с приемами деления многозначного числа на однозначное и записью деления углом; отработка навыков вычислений. | 1 |
| 49 | Деление многозначного числа с нулём посередине и на конце на однозначное число. (С-15) | Рассмотреть способ деления круглых чисел; отработка навыков устных и письменных вычислений.
| 1 |
| 50 | Деление круглых чисел на однозначное число. | Строить и применять алгоритмы деления многозначного числа на однозначное число. Анализировать и интерпретировать данные таблицы. Решать задачи на нахождение периметра треугольника, площади фигур, составленных из прямоугольников. Записывать деление уголком. | 1 |
| 51 | Деление круглых чисел на однозначное число. (С-16) | Рассмотреть способ деления круглых чисел; отработка навыков устных и письменных вычислений. | 1 |
| 52 | Деление на однозначное число с остатком. Деление круглых чисел с остатком. | Строить общий алгоритм деления с остатком многозначных круглых чисел. Выполнять задания поискового и творческого характера. Применять метод моделирования в учебной деятельности. | 1 |
| 53 | Деление на однозначное число (и сводящиеся к нему случаи деления круглых чисел). (С-17) | Закрепление знаний учащихся о приемах деления на однозначное число, отработка навыков устных и письменных вычислений. | 1 |
| 54 | Умножение и деление на многозначное число. | Применять изученные способы действий для решения задач в типовых и поисковых ситуациях. | 1 |
| 55 | Контрольная работа по теме «Умножение и деление многозначных чисел на однозначное» | Контролировать правильность и полноту выполнения изученных способов действий.
| 1 |
| 56 | Работа над ошибками | Выявлять причину ошибки и корректировать ее, оценивать свою работу. | 1 |
| 57 | Преобразование фигур на плоскости. | Выполнять преобразование фигур. Определять вид многоугольников. Устанавливать свойства фигур, симметричных относительно прямой. Чертить симметричные фигуры. | 1 |
| 58 | Симметрия. | Знакомство с новым видом преобразования фигур на плоскости (симметрией); отработка навыков устных и письменных вычислений. | 1 |
| 59 | Построение симметричных фигур на клетчатой бумаге. Палиндромы. | Чертить симметричные фигуры. Наблюдать симметрию в рисунках, буквах словах, текстах, стихах. Собирать материал по заданной теме, свои симметричные фигуры. Составлять узоры с помощью параллельного переноса. | 1 |
| 60 | Повторение и закрепление по теме «Умножение и деление многозначных чисел на однозначные». | Закрепление знаний учащихся о преобразовании фигур на плоскости (симметрия); отработка навыков устных и письменных вычислений.
| 1 |
| 61 | Контрольная работа за 1 полугодие. | Проверить умение делить на однозначное число столбиком, проверить знания по преобразованию фигур. | 1 |
| 62 | Работа над ошибками. | Выявлять причину ошибки и корректировать ее; оценивать свою работу. | 1 |
| 63 | Симметричные фигуры. (С-18) | Закрепление знаний учащихся о преобразовании фигур на плоскости; рассмотрение симметрии фигур относительно прямой l. | 1 |
| 64 | Творческие работы учащихся: «Красота и симметрия». | Проектная деятельность. | 1 |
| 65 | Меры времени. Календарь. Дата. (С-19) | Сравнивать события по времени непосредственно. Устанавливать соотношение между общепринятыми единицами времени. Преобразовывать, складывать, сравнивать и вычитать значения времени. Разрешать житейские ситуации, требующие умения находить значения времени события. | 1 |
| 66 | Меры времени. Дни недели. | Познакомить с мерами времени, научит пользоваться календарём; совершенствовать вычислительные навыки. | 1 |
| 67 | Календарь. Неделя. (С-20) | Преобразовывать, складывать, сравнивать и вычитать значения времени. Использовать календарь, название месяцев, дней недели. Решать задачи на нахождение начала события, завершения его, продолжительности его. | 1 |
| 68 | Таблица мер времени. | Ввести новые понятия - меры времени, работать над умением переводить величины из одних единиц измерения в другие, закреплять навык решения задач. | 1 |
| 69 | Часы. | Определять время по часам. Собирать и представлять информацию по заданному плану и теме. Решать вычислительные примеры, уравнения, простые и составные задачи изученных типов. | 1 |
| 70 | Таблица мер времени. Часы. (С-21) | Ввести понятие новой меры времени- часа, отрабатывать умение переводить величины из одних единиц измерения в другие. Арифметические ребусы. | 1 |
| 71 | Сравнение, сложение и вычитание единиц времени. | Применять простейшие приемы ораторского искусства и оценивать свое умение это делать. Составлять, читать и записывать числовые и буквенные выражения, содержащие все 4 арифметических действия. Находить значение выражения. | 1 |
| 72 | Сравнение, сложение и вычитание единиц времени. (С-22) | Научить учащихся сравнивать, складывать и вычитать единицы времени. Игра роботы. | 1 |
| 73 | Переменная. | Обозначать переменную буквой. Составлять выражения с переменной. Находить в простейших случаях значение выражения с переменной и множество значений выражения с переменной. | 1 |
| 74 | Выражение с переменной. | Дать представление о переменной, научит составлять выражение с переменной. | 1 |
| 75 | Высказывание. | Находить верные и неверные высказывания. Обосновывать в простейших случаях их истинности и ложности. Строить верные и неверные высказывания с помощью логических связок. Выполнять задания поискового и творческого характера. | 1 |
| 76 | Переменная. Высказывание (С-23) | Продолжить работу по составлению выражений с переменной и научить находить их значение по данным задачи. | 1 |
| 77 | Равенство и неравенство. | Определять, обосновывать и опровергать истинность и ложность равенств и неравенств. Различать выражения, равенства и уравнения. Повторять и систематизировать знания и видах и способах решения простых уравнений. Строить и применять алгоритм решения составных уравнений. | 1 |
| 78 | Уравнения. Корень уравнения. Классификация простых уравнений. | Познакомить с определением уравнения, вспомнить и повторить известные виды уравнений, а также ввести новый вид уравнений и научить решать их на основе зависимости между компонентами действий, научить решать задачи с применением уравнений. | 1 |
| 79 | Равенство и неравенство. Уравнения. (С-24) | Решать простые и составные уравнения. Комментировать решение, называя компоненты действий. Решать вычислительные примеры, уравнения, простые и составные задачи. | 1 |
| 80 | Упрощение уравнений. Решение составных уравнений с комментированием по компонентам действий | Решать вычислительные примеры, уравнения, простые и составные задачи. | 1 |
| 81 | Составные уравнения, сводящиеся к цепочке простых. | Систематизировать основные свойства сложения и умножения. Записывать их в буквенном виде, применять для упрощения вычислений. Применять алгоритм обобщения и оценивать свое умение это делать. | 1 |
| 82 | Решение составных уравнений с комментированием по компонентам действий | Применять изученные способы действий для решения задач в типовых и поисковых ситуациях. | 1 |
| 83 | Контрольная работа по теме «Уравнения» | Контролировать правильность и полноту выполнения изученных способов действий. | 1 |
| 84 | Работа над ошибками по теме «Уравнения» | Выявлять причину ошибки и корректировать ее, оценивать свою работу. | 1 |
| 85 | Формула. Формулы площади и периметра прямоугольника: S = a ∙ b, P = (a + b) × 2. | Строить формулы площади и периметра прямоугольника, площади и периметра квадрата, объема прямоугольного параллелепипеда. Составлять таблицы, анализировать и интерпретировать их данные. Обобщать выявленные закономерности и записывать их виде формул. | 1 |
| 86 | Формула объема прямоугольного параллелепипеда: V = a×b ×c. | Познакомить с формулой нахождения объёма прямоугольного параллепипеда и научить применять её при решении задач. | 1 |
| 87 | Формула площади и периметра прямоугольника, объёма прямоугольного параллелепипеда. | Систематизировать частные случаи арифметических действий с 0 и 1. Записывать в буквенном виде, применять для вычислений. Выполнять задания поискового и творческого характера. | 1 |
| 88 | Формула деления с остатком: a=b·c+ r, r | Познакомить с формулой деления с остатком и научить пользоваться ею при решении примеров. Кроссворд. | 1 |
| 89 | Решение задач с использованием формул. | Решать вычислительные примеры, уравнения, простые и составные задачи. Изготавливать модель куба по ее развертке. Строить формулы площади и периметра прямоугольника, площади и периметра квадрата, объема прямоугольного параллелепипеда. | 1 |
| 90 | Обобщение по теме «Формулы фигур» | Ввести формулы для нахождения скорости, времени, пути, научить использовать их при решении задач. Решение задач на логическое мышление. | 1 |
| 91 | Часть 3. Скорость, время, расстояние. | Наблюдать зависимости между величинами «скорость – время - расстояние» при равномерном прямолинейном движении с помощью графических моделей. Строить формулу, использовать ее для решения задач на движение. Моделировать и анализировать условие задач с помощью таблиц. | 1 |
| 92 | Изображение движения на числовом луче. Формула пути: s = v·t. | Совершенствовать навык решение задач на движение, отрабатывать навыки вычислительных приёмов. Арифметические ребусы, решение задач на логическое мышление. | 1 |
| 93 | Решение задач на движение с использованием формулы пути. | Решать вычислительные примеры, уравнения, простые и составные задачи изученных типов. Систематизировать основные свойства вычитания, использовать их для упрощения вычислений. | 1 |
| 94 | Построение формул зависимости между величинами описывающими движение, с использованием таблиц и числового луча. | Устанавливать соотношения между единицами времени, преобразовывать их. Сравнивать, складывать и вычитать значения времени. | 1 |
| 95 | Решение задач на движение с использованием формулы пути, схем и таблиц. | Совершенствовать навык решение задач на движение, отрабатывать навыки вычислительных приёмов. Арифметические ребусы, решение задач на логическое мышление. | 1 |
| 96 | Решение задач на движение с использованием формулы пути, схем и таблиц. | Фиксировать шаги учебной деятельности, определять место и причину затруднения в коррекционной деятельности. Оценивать свое умение это делать. | 1 |
| 97 | Решение задач на движение с использованием формулы пути, схем и таблиц. | Совершенствовать навык решение задач на движение, отрабатывать навыки вычислительных приёмов. Арифметические ребусы, решение задач на логическое мышление. | 1 |
| 98 | Решение задач на движение. | Решать вычислительные примеры, уравнения, простые и составные задачи. Изготавливать модель куба по ее развертке. Строить формулы площади и периметра прямоугольника, площади и периметра квадрата, объема прямоугольного параллелепипеда. | 1 |
| 99 | Решение задач на движение. | Совершенствовать навык решение задач на движение, отрабатывать навыки вычислительных приёмов. Арифметические ребусы, решение задач на логическое мышление. | 1 |
| 100 | Решение задач на движение. | Решать вычислительные примеры, уравнения, простые и составные задачи изученных типов. Систематизировать основные свойства вычитания, использовать их для упрощения вычислений. | 1 |
| 101 | Контрольная работа за 3 четверть по теме «Формулы. Зависимости между величинами, характеризующими процессы движения» | Применять изученные способы действий для решения задач в типовых и поисковых ситуациях. Контролировать правильность и полноту выполнения изученных способов действий. | 1 |
| 102 | Работа над ошибками по теме «Формулы. Зависимости между величинами, характеризующими процессы движения» | Выявлять причину ошибки и корректировать ее, оценивать свою работу. | 1 |
| 103 | Умножение на двузначное число. | Строить и применять алгоритм умножения на двузначное число и сводящихся к нему случаев умножения круглых чисел. Записывать умножения на двузначное число в столбик, проверять правильность выполнения действий с помощью алгоритма и вычислений на калькуляторе. | 1 |
| 104 | Формула стоимости: С = a·n. Решение задач на величины, описывающие процессы купли-продажи с использованием формулы стоимости и таблиц. | Строить формулу стоимости, использовать ее для решения задач на покупку товара. Моделировать и анализировать условие задач с помощью таблиц. | 1 |
| 105 | Умножение на двузначное число. Формула стоимости. | Фиксировать с помощью равенства отношения. Определять делители и кратные заданного числа. Выполнять задания поискового и творческого характера. | 1 |
| 106 | Умножение круглых чисел, сводящееся к умножению на двузначное число. | Решать вычислительные примеры, уравнения, простые и составные задачи изученных типов. | 1 |
| 107 | Решение задач на формулу стоимости. | Систематизировать основные свойства вычитания, использовать их для упрощения вычислений. | 1 |
| 108 | Умножение на двузначное число. Решение задач на формулу стоимости. | Решение задач. Познакомить с понятиями: цена, количество, стоимость, обозначением этих величин символами, научить решать задачи с использованием формулы стоимости. Ввод формулы цена и количества, решение логических задач. | 1 |
| 109 | Умножение на трёхзначное число. | Строить и применять алгоритм умножения на двузначное число и сводящихся к нему случаев умножения круглых чисел. | 1 |
| 110 | Умножение на трёхзначное число. | Записывать умножения на двузначное число в столбик, проверять правильность выполнения действий с помощью алгоритма и вычислений на калькуляторе. | 1 |
| 111 | Умножение на трёхзначное число. | Познакомить с умножением на трёхзначное число в строчку, используя распределительный закон умножения, познакомить с приёмом умножения в столбиком, совершенствовать навык решения задач. Арифметические ребусы. | 1 |
| 112 | Работа, производительность, время работы. Формула работы: А =v×t. | Применять изученные способы действий для решения задач в типовых и поисковых ситуациях. Контролировать правильность и полноту выполнения изученных способов действий. Выявлять причину ошибки и корректировать ее, оценивать свою работу. | 1 |
| 113 | Решение задач на формулу работы. | Познакомить с понятиями: работа, время производительность, научить решать задачи по формулам работы и производительности. | 1 |
| 114 | Решение задач на формулу работы. | Фиксировать с помощью равенства отношения. Определять делители и кратные заданного числа. Выполнять задания поискового и творческого характера. | 1 |
| 115 | Умножение на двузначное и трёхзначное число. Решение задач на формулу пути, стоимости, работы. | Закрепить с учащимися навыки решения задач изученных видов с использованием формул, совершенствовать вычислительные навыки. | 1 |
| 116 | Умножение на двузначное и трёхзначное число. Решение задач на формулу пути, стоимости, работы. | Применять изученные способы действий для решения задач в типовых и поисковых ситуациях.
| 1 |
| 117 | Умножение на двузначное и трёхзначное число. Решение задач на формулу пути, стоимости, работы. | Закрепить с учащимися навыки решения задач изученных видов с использованием формул, совершенствовать вычислительные навыки. | 1 |
| 118 | Контрольная работа по теме «Письменное умножение двузначных чисел» | Контролировать правильность и полноту выполнения изученных способов действий.
| 1 |
| 119 | Работа над ошибками по теме «Письменное умножение двузначных чисел» | Выявлять причину ошибки и корректировать ее, оценивать свою работу. | 1 |
| 120 | Решение задач на формулу пути, стоимости, работы. | Закрепить с учащимися навыки решения задач изученных видов с использованием формул, совершенствовать вычислительные навыки. | 1 |
| 121 | Формула произведения: а = b · c. Классификация простых задач изученных типов. | Строить и применять алгоритм умножения на трехзначное число и сводящихся к нему случаев умножения круглых чисел. Записывать умножения на трехзначное число в столбик, проверять правильность выполнения действий с помощью алгоритма и вычислений на калькуляторе. | 1 |
| 122 | Решение задач на формулу произведения. | Выполнять краткую запись с использованием таблиц. Планировать решение задачи. Выбирать наиболее целесообразный способ решения текстовой задачи. Уметь определять новое от известного, выделять главное, составлять план. | 1 |
| 123 | Классификация задач. | Решать вычислительные примеры, уравнения, простые и составные задачи изученных типов. Систематизировать основные свойства вычитания, использовать их для упрощения вычислений. | 1 |
| 124 | Решение задач разных типов. | Закрепить с учащимися навыки решения задач изученных видов с использованием формул, совершенствовать вычислительные навыки. | 1 |
| 125 | Решение задач разных типов. | Закрепить с учащимися навыки решения задач изученных видов с использованием формул, совершенствовать вычислительные навыки. | 1 |
| 126 | Умножение круглых чисел, сводящееся к умножению на трехзначное число. | Решать вычислительные примеры, уравнения, простые и составные задачи. Изготавливать модель куба по ее развертке. Строить формулы площади и периметра прямоугольника, площади и периметра квадрата, объема прямоугольного параллелепипеда. | 1 |
| 127 | Умножение многозначных чисел. | Контролировать и осуществлять пошаговый контроль правильности и полноты выполнения алгоритма арифметического действия. Работая по плану, сверять свои действия с целью, и при необходимости, исправлять ошибки с помощью учителя. | 1 |
| 128 | Умножение многозначных чисел. | Письменные вычисления. Решение задач. | 1 |
| 129 | Умножение многозначных чисел. | Применять изученные способы действий для решения задач в типовых и поисковых ситуациях. | 1 |
| 130 | Контрольная работа по теме «Умножение многозначных чисел». | Контролировать правильность и полноту выполнения изученных способов действий. | 1 |
| 131 | Повторение. | Выявлять причину ошибки и корректировать ее, оценивать свою работу. | 1 |
| 132 | Повторение. | Письменные вычисления. Решение задач. | 1 |
| 133 | Повторение. | Определять, обосновывать и опровергать истинность и ложность равенств и неравенств. Различать выражения, равенства и уравнения. Повторять и систематизировать знания о видах и способах решения простых уравнений. Строить и применять алгоритм решения составных уравнений. | 1 |
| 134 | Повторение. | Применять изученные способы действий для решения задач в типовых и поисковых ситуациях. | 1 |
| 135 | Переводная и итоговая контрольная работа. | Контролировать правильность и полноту выполнения изученных способов действий. | 1 |
| 136 | Повторение. | Выявлять причину ошибки и корректировать ее, оценивать свою работу. | 1 |
| 137 | Повторение. | Письменные вычисления. Решение задач. | 1 |
| 138 | Повторение. | Сравнивать разные способы вычислений, выбирая удобный. Прогнозировать результат вычислений. | 1 |
| 139 | Повторение. | Работать с информацией: интерпретировать информацию (объяснять, сравнивать и обобщать данные, формулировать выводы и прогнозы). | 1 |
VIII. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
Начальное образование существенно отличается от всех последующих этапов образования, в ходе которого изучаются систематические курсы. В связи с этим и оснащение учебного процесса на этой образовательной ступени имеет свои особенности, определяемые как спецификой обучения и воспитания младших школьников в целом, так и спецификой курса «Математика» в частности.
Возрастные психологические особенности младших школьников делают необходимым формирование моделирования как универсального учебного действия. Оно осуществляется в рамках практически всех учебных предметов начальной школы, но для математики это действие представляется наиболее важным, так как создаёт важнейший инструментарий для развития у детей познавательных универсальных действий. Так, например, большое количество математических задач может быть понято и решено младшими школьниками только после создания адекватной их восприятию вспомогательной модели.
Поэтому принцип наглядности является одним из ведущих принципов обучения в начальной школе, так как именно наглядность лежит в основе формирования умения работать с моделями.
В связи с этим главную роль играют средства обучения, включающие наглядные пособия:
1) натуральные пособия (реальные объекты живой и неживой природы, объекты-заместители);
2) изобразительные наглядные пособия (рисунки, схематические рисунки, схемы, таблицы).
Другим средством наглядности служит оборудование для мультимедийных демонстраций (компьютер, медиапроектор, DVD-проектор, видеомагнитофон и др.). Оно благодаря Интернету и единой коллекции цифровых образовательных ресурсов (например, http://school-collection.edu.ru/) позволяет обеспечить наглядный образ к подавляющему большинству тем курса «Математика».
Наряду с принципом наглядности в изучении курса «Математика» в начальной школе важную роль играет принцип предметности, в соответствии с которым учащиеся осуществляют разнообразные действия с изучаемыми объектами. В ходе подобной деятельности у школьников формируются практические умения и навыки по измерению величин, конструированию и моделированию предметных моделей, навыков счёта, осознанное усвоение изучаемого материала. На начальном этапе (1-2 класс) предусматривается проведение значительного числа предметных действий, обеспечивающих мотивацию, развитие внимания и памяти младших школьников. Исходя из этого, второе важное требование к оснащенности образовательного процесса в начальной школе при изучении математики состоит в том, что среди средств обучения в обязательном порядке должны быть представлены объекты для выполнения предметных действий, а также разнообразный раздаточный материал.
Раздаточный материал для такого рода работ должен включать реальные объекты (различные объекты живой и неживой природы), изображения реальных объектов (разрезные карточки, лото), предметы − заместители реальных объектов (счётные палочки, раздаточный геометрический материал), карточки с моделями чисел.
В ходе изучения курса «Математика» младшие школьники на доступном для них уровне овладевают методами познания, включая моделирование ситуаций, требующих упорядочения предметов и математических объектов (по длине, массе, вместимости и времени), наблюдение, измерение, эксперимент (статистический). Для этого образовательный процесс должен быть оснащён необходимыми измерительными приборами: весами, часами и их моделями, сантиметровыми линейками и т.д.
Литература для учащихся:
Петерсон, Л. Г. Математика. 3 класс. Ч. 1, 2, 3. – М.: Ювента, 2013.
Петерсон, Л. Г., Невретдинова, А. А., Поникарова Т. Ю. Самостоятельные и контрольные работы по математике в начальной школе. – М.: Ювента, 2013.
Литература для учителя:
Методические рекомендации. Петерсон, Л.Г. Математика.3 класс.-М.: Ювента, 2008
Максимова Т.В. Покрочные разработки по математике, 3 класс. К учебному комплекту Л.Г.Петерсон– М: «ВАКО», 2010
Информационные образовательные ресурсы:
Компьютерная программа комплексного мониторинга развития ребёнка «Электронное приложение к учебникам математики Л.Г.Петерсон».
Начальная школа. Уроки Кирилла и Мефодия. Русский язык, математика, окружающий мир. 3 класс. (1DVD). 2009
Начальная школа. Уроки Кирилла и Мефодия. Математика в 2-х частях. 3класс. (DVD-диски). 2008.
Единая коллекция цифровых образовательных ресурсов (http://school-collection.edu.ru/)
Образовательная коллекция. Устный счёт для учеников 1-6 классов (DVD-диск). 2012.
Образовательная коллекция. Интерактивная энциклопедия по математике. Теория и практика для начальной школы. ((DVD-диск). 2012.
Технические средства
Классная доска с набором приспособлений для крепления таблиц, постеров
и картинок.
Настенная доска с набором приспособлений для крепления картинок.
Компьютер
Мультимедийный проектор.
Интерактивная доска.
Видеофильмы, соответствующие тематике программы
Мультимедийные (цифровые) образовательные ресурсы, соответствующие тематике программы.
Сайт «Сеть творческих учителей» http://www.it-n.ru
Единая коллекция «Цифровые образовательные ресурсы» http://school-collection.edu.ru
Сайт: Фестиваль педагогических идей «Открытый урок» http://festival.1september.ru
Сайт «Детские электронные книги и презентации» http://viki.rdf.ru
Информационный образовательный портал http://www.rusedu.ru
Сайты приоритетных национальных проектов http://www.rost.ru
Информационный образовательный портал «Завуч. Инфо» http://zavuch.info/ru
Сайт Министерства образования и науки Российской Федерации http://www.ed.gov.ru -http://www.ed.gov.ru
Педсовет http://pedsovet.org/
Сайт образовательной системы «Школа 2100» - http://www.school2100.ru
Демонстрационные таблицы
3. Л.Г. Петерсон. Математика. Комплект таблиц для начальной школы: 3 класс (В печати.)
Компьютерные и информационно-коммуникативные средства CD-диски «Электронное приложение»
3. В.А. Петерсон, М.А. Кубышева. Электронное приложение к учебникам математики Л.Г. Петерсон. 3 класс.
Учебно-практическое и учебно-лабораторное оборудование
Наборы муляжей овощей и фруктов.
Набор предметных картинок.
Наборное полотно.
Набор, содержащий геометрические тела: куб, шар, конус, прямоугольный
параллелепипед, пирамиду, цилиндр.
Демонстрационная оцифрованная линейка.
Демонстрационный чертёжный угольник.
Демонстрационный циркуль.
40
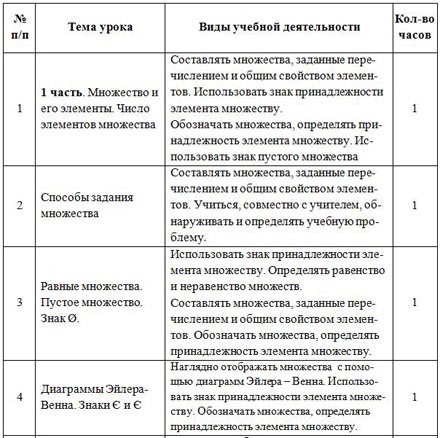

 Получите свидетельство
Получите свидетельство Вход
Вход












 Рабочая программа по математике (3 класс) (0.53 MB)
Рабочая программа по математике (3 класс) (0.53 MB)
 0
0 746
746 12
12 Нравится
0
Нравится
0










